Расчетно-графическая работа №2 Тема: Вычисление определенных интегралов Задание. Вычислить определенные интегралы

1. а)

б)

в)

г)

2. а)

б)

в)

г)

3. а)

б)

в)

г)

4. а)

б)

в)

г)

5. а)

б)

в)

г)

6. а)

б)

в)

г)

7. а)

б)

в)

г)

8. а)

б)

в)

г)

9. а)

б)

в)

г)

10. а)

б)

в)

г)

11. а)

б)

в)

г)

12. а)

б)

в)

г)

13. а)

б)

в)

г)

14. а)

б)

в)

г)

15. а)

б)

в)

г)

16. а)

б)

в)

г)

17. а)

б)

в)

г)

17. а)

б)

в)

г)

Рекомендации по выполнению задания

Для вычисления определенного интеграла находят:

1. Неопределенный интеграл ;

2. Значение интеграла F(x)+С при x=b ,C=0, т.е. вычисляют F(b);

3. Значение интеграла F(x)+C при X=a , C=0 , т.е. вычисляют F(a);

4. Разность F(b)-F(a).

Процесс вычисления виден из формулы

Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов. Числовое значение определенного интеграла зависит от вида функции, стоящей под знаком интеграла, и от значений верхнего и нижнего пределов и не зависит от обозначения переменной.

Пример 1.

.

Решение. .

Пример 2. .

Решение. = = - .

Пример 3. .

Решение. +

+ =

Пример 4. .

Решение. =

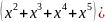
=( -((- + =4.

Подстановка в определенном интеграле

Метод подстановки заключается в том, что для приведения заданного неопределенного интеграла к табличному выражают аргумент через новую переменную, а затем находят неопределенный интеграл и полученный результат снова выражают через начальную переменную. В случае же определенного нет необходимости возвращаться к первоначальной переменной, однако нужно помнить, что, заменяя переменную под знаком интеграла, следует изменить и пределы интегрирования.

Пример 5. .

Решение. Воспользуемся подстановкой u=1- Затем найдем новые пределы интегрирования

= = 2 du=

-2

Пример 6. .

Решение.

.

Пример 7. ^.

Решение. ⁼ =3 =1.

Расчетно-графическая работа №3

Тема: Вычисление площадей криволинейных трапеций

Задание. Вычислить площадь фигуры, ограниченной линиями,

сделать чертеж

1. y=x²+1, y=3-x

2. y=x²–2x+3, y=5- x

3. y= 4x-x², y=4-x

4. y=4x–x², y=0

5. y= -x²+4, y=0

6. y= x²-4x+5, y=5

7. y= 8+2x-x², y=x+6

8. y=4-x², y=3

9. y=3-2x-x², y=1-x

10. y=-x²+6x-5, y= -x+5

11. y=x², y=2x

12. y=x², y=3x

13. y=-x²-4x, y=1, x=-3, x=-1

14. y=3-2x-x², y=0, x=0, x=-2

15. y=–3x²–2, x=1, x=2, y=–1

16. y=x²-4x+5, y=0, x=0, x=4

17. y= x²-4x+6, y=1, x=1, x=3