Приложения производной к решению физических задач

Как известно, производная характеризует мгновенную скорость прямолинейного движения. Однако этим не исчерпывается использование производной. При изучении неравномерно меняющихся величин скорость их изменения всегда выражаются с помощью производной.

Понятие скорости, заимствованное из физики, удобно при исследовании поведения любой функции. Какую бы зависимость ни выражала функция 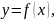отношение 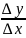есть средняя скорость изменения функции 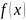относительно изменения аргумента х, а 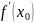– мнгновенная скорость изменения функции при некотором значении

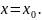
Пример 1. Чему равна скорость изменения функции 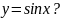Вычислить ее значение для

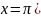
Так как в практических приложениях нас интересует не только сама функция, но и скорость ее изменения, то производная, будучи характеристикой скорости изменения функции, имеет самые широкие практические применения в вопросах физики, химии, геометрии и т.д. Приведем некоторые конкретные примеры использования понятия производной при определении скорости различных процессов.

1. Предположим, что в момент времени t масса еще не распавшегося радиоактивного вещества была равна m, а через некоторое время, в момент 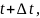масса его уменьшилась (так как часть вещества превратилась в продукт распада) и стала равна 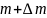(здесь 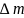отрицательно, поскольку масса радиоактивного вещества с течением времени уменьшается). Таким образом, за время масса имевшегося радиоактивного вещества изминилась на

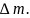
Отношение 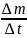представляет собой среднюю скорость распада за промежуток времени 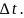Чем меньше этот промежуток, тем точнее указанное отношение выражает мгновенную скорость распада . Поэтому можно сказать, что мгновенная скорость распада в момент времени t равна .

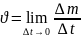2. Мгновенная мощность есть производная 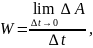где 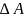– работа, совершаемая за время

3. Если V – объем жидкости, на который действует внешнее давление P, то производная 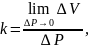дает коэффициент сжатия жидкости при данном давлении.

4. Если твердое тело вращается вокруг оси, то угол поворота 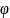есть функция от времени t. Угловая скорость вращения в данный момент t численно равна производной

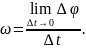
5. Сила тока есть производная 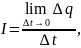где 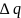– положительный электрический заряд, переносимый через сечение проводника за время

6. Теплоемкость при температуре Т есть производная 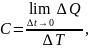где 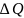- количество теплоты, необходимое для изменения температуры на

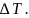
Пример 2. Маховик за время t поворачивается на угол 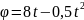(t – в секундах, - в радианах). Определить угловую скорость 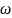в конце 3 – й секунды. Найти момент, когда прекратится вращение.

Решение. Имеем 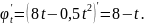Так как 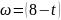рад\с, то при t = 3 получим 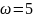(рад\с). Вращение прекратится в момент, когда 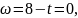т.е. при t = 8c.

Пример 3. Маховик, задерживаемый тормозом, за t с поворачивается на угол 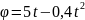(рад). Определить угловую скорость маховика в момент времени t = 2 c и найти момент остановки вращения.

Пример 4. Количество теплоты Q, получаемое некоторым веществом при нагревании его от 0 до Т, определяется по формуле 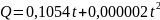(Q – в джоулях, t – в кельвинах). Найти теплоемкость этого вещества при 100К.

Решение. Находим теплоемкость:

С =

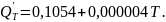
При Т = 100К получим

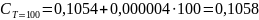(Дж\К).

Пример 5. Закон изменения тепмературы Т тела в зависимости от времени t задан уравнением

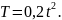
C какой скорости нагревается это тело в момент времени 10с?

Решение. Скорость нагревания тела есть производная температуры Т по времени t:

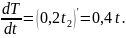
Определим скорость нагревания тела при t = 10

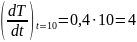(град\с)..

Пример 6. Температура тела Т изменяется в зависимости от времени t по закону 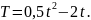С какой скоростью нагревается это тело в момент времени