
- •«Ачинский колледж отраслевых технологий и бизнеса»
- •Методические рекомендации по выполнению практических работ
- •030912 Право и организация социального обеспечения
- •Практическая работа №1
- •Ход работы Область определения функции
- •П ервый замечательный предел
- •Практическая работа №2
- •Ход работы
- •Правила дифференцирования функции
- •1. Найти производные следующих функций:
- •2. Найти производные следующих функций:
- •3. Найти производные следующих функций:
- •4. Найти производные следующих функций:
- •Практическая работа №3
- •Ход работы Дифференцирование сложной функции
- •Практическая работа №4
- •Ход работы
- •Найти производные второго порядка заданных функций:
- •Найти производные третьего порядка заданных функций:
- •Практическая работа №5
- •Ход работы Общая схема исследования функции и построение графика
- •Практическая работа №6
- •Ход работы
- •Практическая работа №7
- •Ход работы
- •Приложения производной к решению физических задач
- •Приложение производной в экономической теории
- •Практическая работа №8
- •Ход работы
- •Основные свойства неопределенного интеграла
- •Основные формулы интегрирования
- •Примеры интегрирования подстановкой
- •Способ интегрирования по частям
- •Практическая работа №9
- •Ход работы
- •Подстановка в определенном интеграле
- •Практическая работа №10
- •Ход работы
- •Нахождения пути, пройденного телом при прямолинейном движении
- •Вычисление работы силы, произведенной при прямолинейном движении тела
- •Вычисления работы, затраченной на растяжение или сжатие пружины
- •Использование понятия определенного интеграла в экономике
- •Практическая работа №11
- •Ход работы Правило вычисления площадей плоских фигур
- •Площади фигур, расположенных над осью
- •Площади фигур, расположенных полностью или частично под осью
- •Площади фигур, прилегающих к оси
- •Симметрично расположенные плоские фигуры
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси ох
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси оу
- •Практическая работа №12
- •Ход работы Определение вероятности события
- •Теорема сложения вероятностей
- •Условная вероятность
- •Практическая работа №13
- •Ход работы Задачи математической статистики
- •Практическая работа №14
- •Ход работы
- •Список используемых источников
1. Найти производные следующих функций:
1.
y=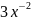
2.
Y=
3.
Y=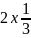
4.
y=2x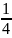
5.
Y=3x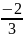
6.
Y=5x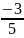
7.
y=5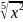
8.
Y=3
9.
Y=
10.
y=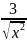
11.
Y=
12.
Y=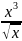
13.
y=
14.
Y=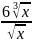
15.
Y=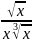
2. Найти производные следующих функций:
у = -
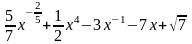 ;
;
у =
 ;
;у =
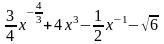 ;
;
у =
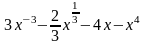 -
-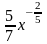 ;
;у =
 ;
;
у =
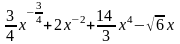 +
+
3. Найти производные следующих функций:
y=(

f(x)=(x+2)(

F(t)=(
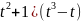
F(u) = (
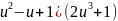
y=(
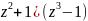
Y=

у =
 ;
;
у =

у =
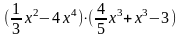 ;
;
у =
 ;
;у =
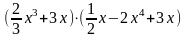 ;
;
у = ;
у =
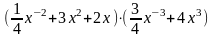
у =5ctgx × arctgx;
у = 2х × arcsinх;
у =3сosx × arcctgx
у = -2tgx × arcsinx;
у = -2tgx × arcsinx;
у= tgx (x3-3x2+1)
у= tgx (x2-3x+2)
у= tgx (2x3-x2+5)
у= tgx (2x3-x2+1)
4. Найти производные следующих функций:
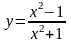

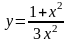

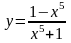
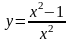
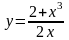

у =
 ;
;
у =
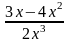 ;
;
у =
 ;
;у =
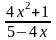 ;
;у =
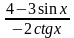 ;
;
у =
 ;
;у =
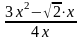 ;
;
у =
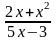 ;
;
Практическая работа №3
Тема: Решение задач на отыскание производной сложной функции.
Цель: Научиться находить производную простой и сложной функции, строить график функции с использованием производной.
Ход работы Дифференцирование сложной функции
Пусть
дана сложная функция
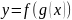 тогда, если функция
тогда, если функция
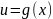 имеет производную в некоторой точке
,
а функция
имеет производную в некоторой точке
,
а функция
 имеет производную в точке
,
тогда
имеет производную в точке
,
тогда
 .
.
Доказательство
 .
.
Пример 1. Найти производные:

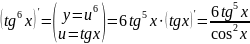
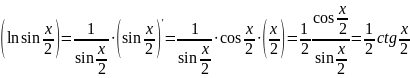
 =
=
 .
.
Задания для самостоятельного решения
Найти производные сложных функций
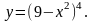
y= (x4+2)6
y= (2x4+3)80
y= (x3+2)7
y= (3x4+5)90
y= (2x4+3)8
y= (x3+4)100
y= (x3+2)10
y= (2x5+6)80


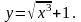
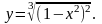


y=sin(x4+2x+1)
y=sin(3x4+x+1)
y=sin(3x+x2+1)
y=arctg(5x2)
y=arctg(x3)
y=arctg(3-x2)
y=ln(4x2+1)
y=ln(2x)
y=ln(5x+4)
Практическая работа №4
Тема: Вычисление производных второго и высших порядков
Цель: Научиться находить производные функции высших порядков.
Ход работы
Производную
от данной функции часто называют первой
производной (или
производной
первого порядка).
Очевидно, что производная также является
функцией, и если она дифференцируема,
то от нее, в свою очередь, можно взять
производную, которую называют второй
производной (или
производной
второго порядка) и
обозначают
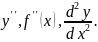
Производной
третьего порядка (или
третьей
производной) называют
производную от второй производной. Ее
обозначают

Например,
для функции
 имеем
имеем

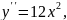
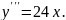
Вообще,
производной
n-го
порядка от
функции
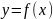 называется производная от произведной
(n-1)
– го порядка. Ее обозначают:
называется производная от произведной
(n-1)
– го порядка. Ее обозначают:
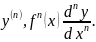 Таким образом, производную n
– го порядка можно найти последовательным
дифференцированием данной функции.
Таким образом, производную n
– го порядка можно найти последовательным
дифференцированием данной функции.
Решение примеров
1. Найти производную второго порядка:
![]() .
.
Сначала найдем производную первого порядка:
![]() .
.
Теперь найдем производную от производной первого порядка. Это и будет производная второго порядка:
![]() .
.
2. Найти производную третьего порядка:
![]() ,
,
Найдем производную первого порядка:
![]() ,
,
Теперь найдем производную второго порядка:
![]() ,
,
И наконец найдем производную от производной второго порядка, это будет производная третьего порядка:
![]()
.
3. Найти производную n-го порядка функции:
![]() .
.
Находим производную первого порядка:
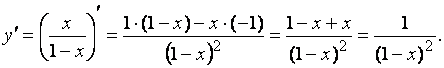
Теперь находим производную второго порядка:
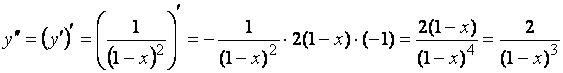 .
.
Находим производною третьего порядка:
 .
.
Находим производную четвертого порядка:
 :
:
Тогда пятая производная имеет вид:
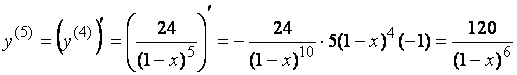 .
.
Задания для самостоятельного решения
