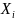- •«Ачинский колледж отраслевых технологий и бизнеса»
- •Методические рекомендации по выполнению практических работ
- •030912 Право и организация социального обеспечения
- •Практическая работа №1
- •Ход работы Область определения функции
- •П ервый замечательный предел
- •Практическая работа №2
- •Ход работы
- •Правила дифференцирования функции
- •1. Найти производные следующих функций:
- •2. Найти производные следующих функций:
- •3. Найти производные следующих функций:
- •4. Найти производные следующих функций:
- •Практическая работа №3
- •Ход работы Дифференцирование сложной функции
- •Практическая работа №4
- •Ход работы
- •Найти производные второго порядка заданных функций:
- •Найти производные третьего порядка заданных функций:
- •Практическая работа №5
- •Ход работы Общая схема исследования функции и построение графика
- •Практическая работа №6
- •Ход работы
- •Практическая работа №7
- •Ход работы
- •Приложения производной к решению физических задач
- •Приложение производной в экономической теории
- •Практическая работа №8
- •Ход работы
- •Основные свойства неопределенного интеграла
- •Основные формулы интегрирования
- •Примеры интегрирования подстановкой
- •Способ интегрирования по частям
- •Практическая работа №9
- •Ход работы
- •Подстановка в определенном интеграле
- •Практическая работа №10
- •Ход работы
- •Нахождения пути, пройденного телом при прямолинейном движении
- •Вычисление работы силы, произведенной при прямолинейном движении тела
- •Вычисления работы, затраченной на растяжение или сжатие пружины
- •Использование понятия определенного интеграла в экономике
- •Практическая работа №11
- •Ход работы Правило вычисления площадей плоских фигур
- •Площади фигур, расположенных над осью
- •Площади фигур, расположенных полностью или частично под осью
- •Площади фигур, прилегающих к оси
- •Симметрично расположенные плоские фигуры
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси ох
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси оу
- •Практическая работа №12
- •Ход работы Определение вероятности события
- •Теорема сложения вероятностей
- •Условная вероятность
- •Практическая работа №13
- •Ход работы Задачи математической статистики
- •Практическая работа №14
- •Ход работы
- •Список используемых источников
Практическая работа №13
Тема: Вычисление числовых характеристик случайных величин
Цель: Научиться решать задачи на вычисление вероятностей событий и числовых характеристик случайных величин
Ход работы Задачи математической статистики
Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных - результатов наблюдений.
Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений; следовательно, математическая статистика имеет дело с массовыми явлениями.
Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования.
Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования, в ходе исследования и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности
Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов.
Генеральная и выборочная совокупность статистических данных
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.
Качественными признаками объект обладает либо не обладает. Они не поддаются непосредственному измерению (например, спортивная специализация, квалификация, национальность, территориальная принадлежность и т. п.).
Количественные признаки представляют собой результаты подсчета или измерения. В соответствии с этим они делятся на дискретные и непрерывные.
Иногда проводиться сплошное обследование, т.е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Различают генеральную и выборочную совокупности.
Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов.
Генеральной (основной) совокупностью называют совокупность объектов из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n =100. Число объектов генеральной совокупности N значительно превосходит объем выборки n .
Способы выборки
При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.
Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается.
На практике обычно пользуются бесповторным случайным отбором.
Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли (выборка должна правильно представлять пропорции генеральной совокупности) - выборка должна быть репрезентативной (представительной).
Выборка будет репрезентативной, если:
каждый объект выборки отобран случайно из генеральной совокупности;
все объекты имеют одинаковую вероятность попасть в выборку.
Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение . Это постоянные величины, которые можно оценить по выборочным данным.
Одна из самых важных числовых характеристик случайной величины есть математическое ожидание.
Если известна дискретная случайная величина X, закон распределения которой имеет вид
Значения хi |
X1 |
X2 |
… |
Xn |
Вероятности рi |
P1 |
P2 |
… |
Pn |
то математическим ожиданием (или средним значением) дискретной величины X называется число М(Х)=x1p1 +x2p2 + ... + хnрn.
Таким образом, математическое ожидание дискретной случайной величины X равно сумме произведений возможных значений этой величины на их вероятности.
Пример 1. Найти математическое ожидание дискретной случайной величины, зная закон ее распределения:
Х |
5 |
4 |
3 |
p |
0,2 |
0,5 |
0,3 |
Решение. По формуле находим математическое ожидание:
M (X) = 5*0,2 + 4*0,5 + 3*0,3 = 3,3.
Если дискретная случайная величина принимает счетное множество возможных значений, то
|
|
На практике часто приходится оценить рассеяние возможных значений случайной величины вокруг ее среднего значения.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D (X) = M [X - M (X)]2. |
|
Пример 2. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
Х |
1 |
2 |
5 |
p |
0,3 |
0,5 |
0,2 |
Решение. По формуле находим математическое ожидание:
M (X) = 1*0,3 + 2*0,5 + 5*0,2 = 2,3.
Используя формулу записываем все возможные значения квадрата отклонения:
[X1 - M (X)]2 = (1 - 2,3)2 = 1,69;
[X2 - M (X)]2 = (2 - 2,3)2 = 0,09;
[X3 - M (X)]2 = (5 - 2,3)2 = 7,29.
Тогда закон распределения квадрата отклонения имеет следующий вид:
[X - M (X)]2 |
1,69 |
0,09 |
7,29 |
p |
0,3 |
0,5 |
0,2 |
По формуле находим дисперсию:
D (X) = 1,69*0,3 + 0,09*0,5 + 7,29*0,2 = 2,01.
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:
D (X) = M (X2) - [M (X)]2 |
|
Пример 3. Найти дисперсию случайной величины X, которая задана следующим законом распределения:
Х |
2 |
3 |
5 |
p |
0,1 |
0,6 |
0,3 |
Решение. По формуле находим математическое ожидание:
M (X) = 2*0,1 + 3*0,6 + 5*0,3 = 3,5.
Закон распределения случайной величины X2:
Х2 |
4 |
9 |
25 |
p |
0,1 |
0,6 |
0,3 |
Математическое ожидание М(Х2):
M (X) = 4*0,1 + 9*0,6 + 25*0,3 = 13,3.
По формуле находим дисперсию:
D (X) = 13,3 - (3,5)2 = 1,05.
Средним квадратическим отклонением случайной величины Х называется корень квадратный из ее дисперсии:
|
|
Пример 4. Дан закон распределения случайной величины X.
xi |
0 |
1 |
2 |
3 |
pi |
0.2 |
0.3 |
0.4 |
0.1 |
Вычислите математическое ожидание, дисперсию, среднее квадратическое отклонение случайной величины.
Решение. Математическое ожидание M[X]. M[x] = 0*0.2 + 1*0.3 + 2*0.4 + 3*0.1 = 1.4 Дисперсию находим по формуле d = ∑x2ipi - M[x]2. Дисперсия D[X]. D[X] = 02*0.2 + 12*0.3 + 22*0.4 + 32*0.1 - 1.42 = 0.84 Среднее квадратическое отклонение σ(x). σ(x) = 0.92
Пример 5. Дано распределение дискретной случайной величины X. Построить функцию распределения F (x). Найти математическое ожидание и среднее квадратическое отклонение .
Xi |
4 |
6 |
8 |
9 |
Pi |
0.3 |
0.1 |
0.1 |
0.5 |
Решение.
Функция
распределение равна F
(x)
= P
(X
< x)
=
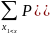 )
=
)
=
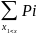 .
Отсюда
.
Отсюда
F(x)
=

Математическое ожидание дискретной случайной величины X равно
М(Х)=
∑
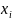
 = 4*0.3+6*0.1+8*0.1+9*0.5 = 7.
= 4*0.3+6*0.1+8*0.1+9*0.5 = 7.
Дисперсия дискретной случайной величины X равна
 =M
[
=M
[ ]
-
]
-
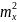 =
=
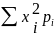 -
=
-
=
 * 0,3 +
* 0,3 +
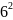 * 0,1 +
* 0,1 +
 * 0,1 +
* 0,1 +
 *0,5 -7,
*0,5 -7,
 =4.89
=4.89
Отсюда среднее квадратическое отклонение равно
 =
=
 =
=
 = 2.211.
= 2.211.
Пример 6. Сделано два высоко рисковых вклада : 10тыс. руб. в компанию А и 15 тыс. руб. в компанию В. Компания А обещает 10%годовых, но может «лопнуть» с вероятностью 0,5 компания В обещает 5%годовых, но может «лопнуть» с вероятностью 0,25. Составить закон распределения случайной величины – общей суммы прибыли (убытка), полученной от двух компаний через год, определить ожидаемую доходность и уровень риска.
Решение.
Возможно
четыре исхода:
 – обе компании «не лопнули»;
– обе компании «не лопнули»;
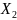 – компания А «не лопнула», а компания
«лопнула»;
– компания А «не лопнула», а компания
«лопнула»;
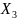 – компания А «лопнула», а компания В
«не лопнула»;
– компания А «лопнула», а компания В
«не лопнула»;
 – обе компании «лопнули». Поскольку
компании работают не зависимо друг от
друга, то по теореме умножения вероятностей
найдём вероятности этих исходов:
– обе компании «лопнули». Поскольку
компании работают не зависимо друг от
друга, то по теореме умножения вероятностей
найдём вероятности этих исходов:
P( ) = 0.5 *0.75=0.375;
P( ) =0.5*0.25=0.125;
P( ) =0.5*0.75=0.375;
P( ) =0.5*0.25=0.125.
Доходы (убыток) от вложения денег:
- при исходе составит 10*0,1+15*0,05=1,75тыс. руб.;
- при исходе составит10*0,1-15=-14 тыс. руб.;
- при исходе составит-10+15*0,05=-9,25 тыс. руб.;
- при исходе составит-10-15=-25 тыс. руб.
Отсюда закон распределения случайной величины – общей суммы прибыли (убытка), полученной от двух компаний через год, имеет вид:
x= |
1.75 |
-14 |
-9.25 |
-25 |
=P(x= ) |
0.375 |
0.125 |
0.375 |
0.125 |
Ожидаемая доходность равна математическому ожиданию полученной случайной величины:
 =M[X]
=
=M[X]
=
 = -7,6875 тыс. руб.
= -7,6875 тыс. руб.
Уровень риска оценим через среднее квадратическое отклонение данной случайной величины:
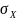 =
=
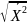 -
(
-
(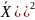 =
=
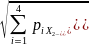 =
=
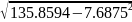 =
= 8.761
тыс. руб.
8.761
тыс. руб.
Задачи для самостоятельного решения
1. Случайная величина X задана рядом распределения. Вычислить математическое ожидание случайной величины М(х), дисперсию D[x], среднее квадратическое отклонение.
а)
xi |
0 |
1 |
2 |
3 |
4 |
pi |
0.5 |
0.3 |
0.15 |
0.03 |
0.02 |
б)
xi |
0 |
1 |
2 |
3 |
pi |
0,1 |
0,4 |
0,3 |
0,2 |
в)
xi |
0 |
1 |
2 |
pi |
0,6 |
0,2 |
0,2 |
г)
xi |
2 |
5 |
8 |
pi |
0,4 |
P2 |
0,1 |
2. По заданному закону распределения дискретной случайной величины X найти ее среднее квадратическое отклонение, получить функцию распределения F(x) , построить многоугольник распределения вероятностей.
а)
|
8 |
12 |
18 |
24 |
30 |
|
0,3 |
0,1 |
0,3 |
0,2 |
0,1 |
|
14 |
18 |
23 |
28 |
30 |
|
0,1 |
0,2 |
0,2 |
0,1 |
0,4 |