Вычисление объема тела, образованного вращением плоской фигуры вокруг оси ох
Пример 6
Вычислить
объем тела, полученного вращением
фигуры, ограниченной линиями 
, 
вокруг
оси 
.
Решение: Как
и в задаче на нахождение площади, решение
начинается с чертежа плоской фигуры.
То есть, на плоскости 
необходимо
построить фигуру, ограниченную
линиями
,
,
при этом не забываем, что уравнение
задаёт
ось
.
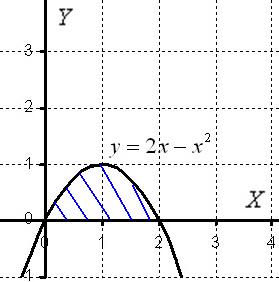
Объем тела вращения можно вычислить по формуле:
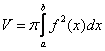
Вычислим
объем тела вращения, используя данную
формулу:
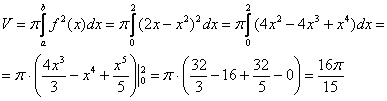
Ответ: 
Пример 7
Вычислить
объем тела, полученного при вращении
вокруг оси абсцисс фигуры, ограниченной
линиями 
, 
, 
и 
Решение: Изобразим
на чертеже плоскую фигуру, ограниченную
линиями
,
,
,
,
не забывая при этом, что уравнение
задает
ось 
:
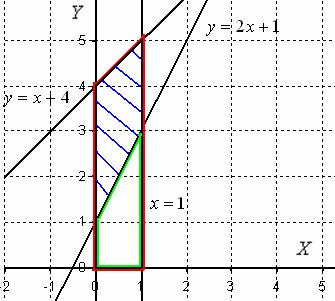
Искомая фигура заштрихована синим цветом. При её вращении вокруг оси получается такой сюрреалистический бублик с четырьмя углами.
Объем тела вращения вычислим как разность объемов тел.
Сначала
рассмотрим фигуру, которая обведена
красным цветом. При её вращении вокруг
оси
получается
усеченный конус. Обозначим объем этого
усеченного конуса через 
.
Рассмотрим
фигуру, которая обведена зеленым цветом.
Если вращать данную фигуру вокруг
оси
,
то получится тоже усеченный конус,
только чуть поменьше. Обозначим его
объем через 
.
И,
очевидно, разность объемов 
–
в точности объем нашего «бублика».
Используем стандартную формулу для нахождения объема тела вращения:
1)
Фигура, обведенная красным цветом
ограничена сверху прямой
,
поэтому:
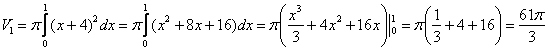
2)
Фигура, обведенная зеленым цветом
ограничена сверху прямой
,
поэтому:
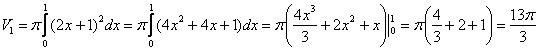
3)
Объем искомого тела вращения: 
Ответ: 
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси оу
Пример 8
Дана
плоская фигура, ограниченная
линиями 
, 
, 
.
1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси .
Решение: Задача состоит из двух частей. Начнем с площади.
1) Выполним чертёж:
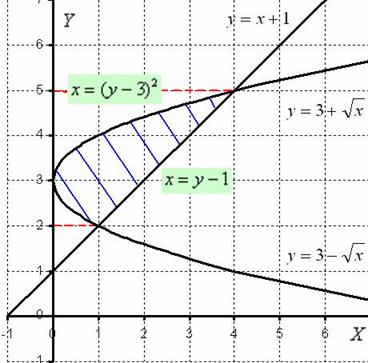
Легко заметить, что функция задает верхнюю ветку параболы, а функция – нижнюю ветку параболы. Перед нами тривиальная парабола, которая «лежит на боку».
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.
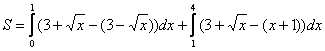
Ответ: 
Для нахождения объема тела вращения будем интегрировать по оси . Сначала нужно перейти к обратным функциям.
Вращаем фигуру, обведенную красным цветом, вокруг оси , в результате получается усеченный конус. Обозначим этот объем через .
Вращаем фигуру, обведенную зеленым цветом, вокруг оси и обозначаем через объем полученного тела вращения.
Объем нашей бабочки равен разности объемов .
Используем
формулу для нахождения объема тела
вращения:
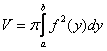
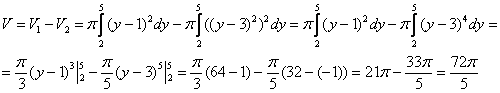
Ответ: 
Практическая работа №12
Тема: Решение задач военной тематики на вычисление вероятностей событий и числовых характеристик случайных величин
Цель: Научиться решать задачи на вычисление вероятностей событий и числовых характеристик случайных величин