Вычисления работы, затраченной на растяжение или сжатие пружины

Согласно закону Гука, сила F, необходимая для растяжения или сжатия пружины, пропорциональна величине растяжения или сжатия.

Пусть x – величина растяжения или сжатия пружины. Тогда 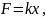где – коэффициент пропорциональности, зависящий от свойства пружины.

Работа на участке 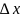выразится формулой 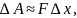а вся затраченная работа – формулой

Или

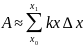
Если , то погрешность величины работы стремится к нулю. Для нахождения истинной величины работы следует перейти к пределу:

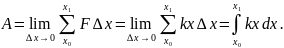
Итак,

Пример 6. какую работу совершает сила в 10 Н при растяжении пружины на 2 см.

Решение. по закону Гука F , растягивающая пружину, пропорциональна растяжению пружины, т.е. F=kx. Используя условие, находим 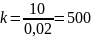(H\м), т.е. F=500x. Согласно формуле (3), получим

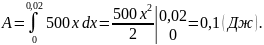
Пример 7. Сила в 60 Н растягивает пружину на 2 см. первоначальная длина пружины равна 14 см. какую работу нужно совершить, чтобы растянуть ее до 20 см?

Решение. Имеем 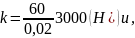следовательно, F=3000x. Так как пружину требуется растянуть на 0,06 (м), то

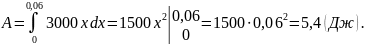
Использование понятия определенного интеграла в экономике

Рассмотрим другие примеры использования интеграла в экономике.

Если в функции Кобба - Дугласа считать, что затраты труда есть линейная зависимость от времени, а затраты капитала неизменны, то она примет вид . Тогда объём выпускаемой продукции за Т лет составит:

Q= .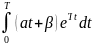

Пример 8. Найти объём продукции, произведенной за 4 года, если функция Кобба – Дугласа имеет вид = .

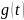Решение. По формуле (11.34) объём Q произведенной продукции равен

Q= .

Используем метод интегрирования по частям. Пусть u=t+1, . Тогда , .

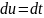Следовательно,

Q=

(усл.ед.)

И сследуя кривую Лоренца-зависимость процента доходов от процента имеющего их населения (кривую ОВА). Мы можем оценить степень неравенства в распределении доходов населения. При равномерном распределении доходов кривая Лоренца вырождается в прямую- биссектрису ОА, поэтому площадь

фигуры ОАВ между биссектрисой ОА и кривой Лоренца, отнесенная к площади треугольника ОАС (коэффициент Джини), характеризует степень неравенства в распределении доходов населения.

Пример 9. По данным исследований в распределении доходов в одной из стран кивая Лоренца ОВА может быть описана уравнением =1-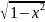 , где - доля населения, - доля расходов населения. Вычислить коэффициент Джини.

, так как = .

= .

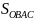Поэтому .

С помощью замены, например 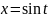можно вычислить

=π/4. Итак, коэффициент Джини =2 .

Достаточно высокое значение показывает существенно неравномерное распределение доходов среди населения в рассматриваемой стране.

Определение начальной суммы по ее конечной величине, полученной через время t (лет) при годовом проценте (процентной ставке) p, называется дисконтированием. Задачи такого рода встречаются при определении экономической эффективности капитальных вложений.

Пусть 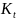- конечная сумма, полученная за t лет, и - дисконтируемая (начальная) сумма, которую в финансовом анализе называют также современной суммой. Если проценты простые, то 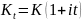, где 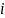= p/100- удельная процентная ставка. Тогда . В случае сложных процентов и потому .

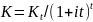Пусть поступающий ежегодно доход изменяется во времени и описывается функцией 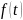и при удельной норме процента, равной , процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход за время Т вычисляется по формуле:

.

Пример 10. определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные (базовые) капиталовложения составили 10 млрд. руб., и намечается ежегодно увеличивать капиталовложения на 1 млрд.руб.

Решение. Очевидно, что капиталовложения задаются функцией . Тогда по формуле (11.35.) дисконтированная сумма капиталовложений .

Интегрируя, получим 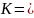30,5 млрд.руб. это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млрд.руб. равносильны одновременным первоначальным вложениям 30,5 млрд.руб. при той же, начисляемой непрерывно, процентной ставке.

Пусть известна функция 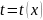, описывающая изменение затрат времени на изготовление изделия в зависимости от степени освоения производства, где - порядковый номер изделия в партии. Тогда среднее время , затраченное на изготовление одного изделия в период освоения от 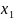до изделий, вычисляется по теореме о среднем:

.

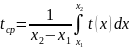Что касается функции изменения затрат времени на изготовление изделий , то часто она имеет вид

,

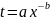где 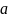- затраты времени на первое изделие, 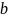- показатель производственного процесса.

Пример 11. найти среднее время, затраченное на освоение одного изделия в период освоения от до изделий, полагая в формуле (11.40) (мин.), .

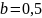Решение. Используя формулу (11.37), получаем

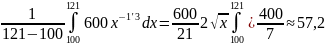= (мин.)

Пример 12. Определить объем продукции, произведенной рабочим за третий час рабочего дня, если производительность труда характеризуется функцией

f(t) = 3/(3t +1) + 4.

Решение. Если непрерывная функция f(t) характеризует производительность труда рабочего в зависимости от времени t, то объем продукции, произведенной рабочим за промежуток времени от t₁ до t₂ будет выражаться формулой

V = .

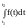В нашем случае

V =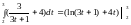 = ln 10 + 12 - ln 7 - 8 = ln 10/7 + 4.

Пример 13. Определить запас товаров в магазине, образуемый за три дня, если поступление товаров характеризуется функцией f(t) = 2t + 5.

Решение. Имеем:

V = .