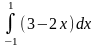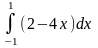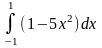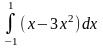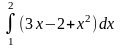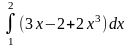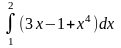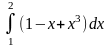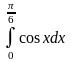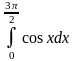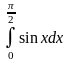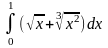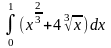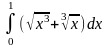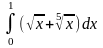Ход работы
Для
вычисления определенного интеграла
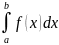находят:
Неопределенный интеграл
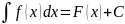;Значение интеграла F(x)+С при x=b ,C=0, т.е. вычисляют F(b);
Значение интеграла F(x)+C при X=a , C=0 , т.е. вычисляют F(a);
Разность F(b)-F(a).
Процесс вычисления виден из формулы
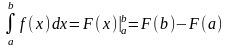
Все методы интегрирования, используемые при нахождении неопределенных интегралов, применяются и при вычислении определенных интегралов. Числовое значение определенного интеграла зависит от вида функции, стоящей под знаком интеграла, и от значений верхнего и нижнего пределов и не зависит от обозначения переменной.
Пример 1.
.
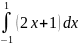Решение.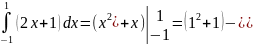
.
Пример
2.
.
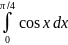Решение.
=
=
-
.
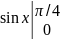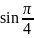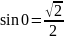Пример
3.
.
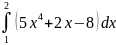Решение.
+
+
=
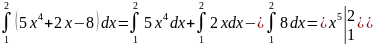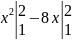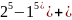
Пример
4.
.
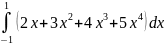Решение.
=
=(
-((-
+
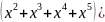
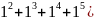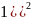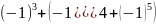=4.
Подстановка в определенном интеграле
Метод подстановки заключается в том, что для приведения заданного неопределенного интеграла к табличному выражают аргумент через новую переменную, а затем находят неопределенный интеграл и полученный результат снова выражают через начальную переменную. В случае же определенного нет необходимости возвращаться к первоначальной переменной, однако нужно помнить, что, заменяя переменную под знаком интеграла, следует изменить и пределы интегрирования.
Пример
5.
.
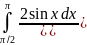Решение.
Воспользуемся подстановкой u=1-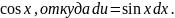
Затем найдем новые пределы интегрирования
=
=
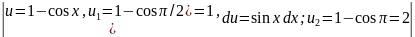2
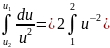du=
-2
Пример
6.
.
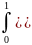Решение.
.
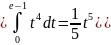Пример
7.
.
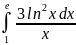Решение.
=
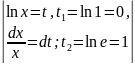=3
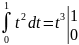=1.
Задания для самостоятельного решения
Практическая работа №10
Тема: Решение задач прикладного характера с применением методов интегрирования
Цель: Научиться находить определенный интеграл
Ход работы
Схема решения задач на приложения определенного интеграла
С помощью определенного интеграла можно решать различные задачи физики, механики и т.д., которые трудно или невозможно решить методами элементарной математики.
Так, понятие определенного интеграла применяется при решении задач на вычисление работы переменной силы, давление жидкости на вертикальную поверхность, пути, пройденного телом, имеющим переменную скорость, и ряд других.
Несмотря на разнообразие этих задач, они объединяются одной и той же схемой рассуждений при их решении. Искомая величина (путь, работа, давление и т.д.) соответствует некоторому промежутку изменения переменной величины, которая является переменной интегрирования. Эту переменную величину обозначают через х, а промежуток ее изменения – через [a, b].
Отрезок [a, b] разбивают на n равных частей, в каждой из которых можно пренебречь изменением переменной величины. Этого можно добиться при увеличении числа разбиений отрезка. На каждой такой части задачу решают по формулам для постоянных величин.
Далее
составляют сумму (интегральную сумму),
выражающую приближенное значение
искомой величины. Переходя к пределу
при
,
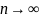находят искомую величину I
в виде интеграла
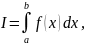
где f(x) – данная по условиям задачи функция ( сила, скорость и т. д. ).