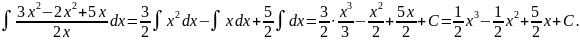- •«Ачинский колледж отраслевых технологий и бизнеса»
- •Методические рекомендации по выполнению практических работ
- •030912 Право и организация социального обеспечения
- •Практическая работа №1
- •Ход работы Область определения функции
- •П ервый замечательный предел
- •Практическая работа №2
- •Ход работы
- •Правила дифференцирования функции
- •1. Найти производные следующих функций:
- •2. Найти производные следующих функций:
- •3. Найти производные следующих функций:
- •4. Найти производные следующих функций:
- •Практическая работа №3
- •Ход работы Дифференцирование сложной функции
- •Практическая работа №4
- •Ход работы
- •Найти производные второго порядка заданных функций:
- •Найти производные третьего порядка заданных функций:
- •Практическая работа №5
- •Ход работы Общая схема исследования функции и построение графика
- •Практическая работа №6
- •Ход работы
- •Практическая работа №7
- •Ход работы
- •Приложения производной к решению физических задач
- •Приложение производной в экономической теории
- •Практическая работа №8
- •Ход работы
- •Основные свойства неопределенного интеграла
- •Основные формулы интегрирования
- •Примеры интегрирования подстановкой
- •Способ интегрирования по частям
- •Практическая работа №9
- •Ход работы
- •Подстановка в определенном интеграле
- •Практическая работа №10
- •Ход работы
- •Нахождения пути, пройденного телом при прямолинейном движении
- •Вычисление работы силы, произведенной при прямолинейном движении тела
- •Вычисления работы, затраченной на растяжение или сжатие пружины
- •Использование понятия определенного интеграла в экономике
- •Практическая работа №11
- •Ход работы Правило вычисления площадей плоских фигур
- •Площади фигур, расположенных над осью
- •Площади фигур, расположенных полностью или частично под осью
- •Площади фигур, прилегающих к оси
- •Симметрично расположенные плоские фигуры
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси ох
- •Вычисление объема тела, образованного вращением плоской фигуры вокруг оси оу
- •Практическая работа №12
- •Ход работы Определение вероятности события
- •Теорема сложения вероятностей
- •Условная вероятность
- •Практическая работа №13
- •Ход работы Задачи математической статистики
- •Практическая работа №14
- •Ход работы
- •Список используемых источников
Практическая работа №8
Тема: Решение задач по интегральному исчислению
Цель: Научиться находить неопределенный интеграл.
Ход работы
Функцию, восстанавливаемую по заданной ее производной или дифференциалу, называют первообразной.
Определение. Дифференцируемая функция F’(x) называется первообразной для функции f(x) на заданном промежутке, если для всех x ∈ R из этого промежутка справедливо равенство F’(x)=f(x).
Из этого определения вытекает, что всякая функция по отношению к своей производной является первообразной.
Так,
функция F’(x)=x2
есть
первообразная функция f(x)=2
на
интервале(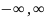 ),
поскольку
для всех x∈R
имеет
место равенство F’(x)=(x2)’=2x.
),
поскольку
для всех x∈R
имеет
место равенство F’(x)=(x2)’=2x.
Основные свойства неопределенного интеграла
Рассмотрим сначала основные свойства неопределенного интеграла.
1.Производная неопределенного интеграла равна подынтегральной функции, т.е.
(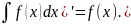
2.Постоянный множитель подынтегрального выражения можно вынести за знак интеграл, т.е.
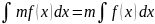
где m- постоянная величина, не равная нулю.
3.Интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от этих функций, т.е.
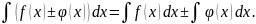
4.Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.
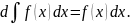
5.Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С, т. е.
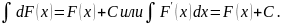
Основные формулы интегрирования
Формулы
интегрирования получаются обращением
соответствующих формул дифференцирования.
Выпишем в таблицу основные интегралы. 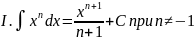
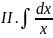 =
=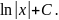
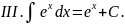
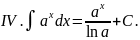
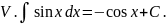
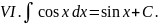
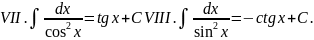
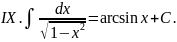
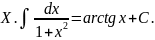
Интегралы, приведенные в этой таблице, называются табличными интегралами.
Для вывода этих формул, как уже отмечалось, используется свойство 5 неопределенного интеграла, а именно дифференцирование правой части равенства. Производная правой части равенства дает подынтегральную функцию, а дифференциал - подынтегральное выражение.
Примеры:
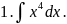
Решение.
Применим формулу
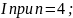
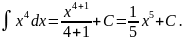
Проверка: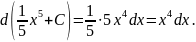 Получили подынтегральное выражение;
следовательно, интеграл найден
верно.
Получили подынтегральное выражение;
следовательно, интеграл найден
верно.
2.
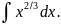
Решение.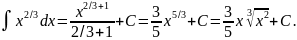
Проверка.
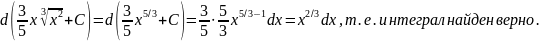
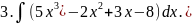
Решение.
Применяя свойства 2 и 3, а затем формулу
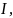 получим
получим
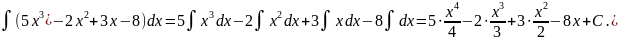
Здесь С- алгебраическая сумма четырех произвольных постоянных слагаемых, являющихся составной частью каждого интеграла.
Продифференцировав этот результат, получим подынтегрального выражение, т.е. решение верное.
4.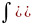
Решение.
Дифференцированием результата легко убедиться, что решение верное.
5.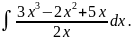
Решение.