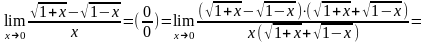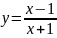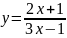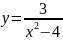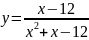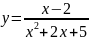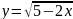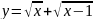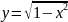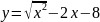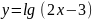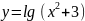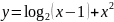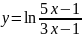Краевое государственное бюджетное образовательное учреждение
среднего профессионального образования
(среднее специальное учебное заведение)
«Ачинский колледж отраслевых технологий и бизнеса»
Плотникова Елена Антоновна
Методические рекомендации по выполнению практических работ
по дисциплине математика
для студентов специальности
030912 Право и организация социального обеспечения
Ачинск
2012 год
Рассмотрено на заседании
Предметно-цикловой комиссии ОГСЭиЕН
Протокол №_______
Председатель предметно-цикловой комиссии
_______________ /Плотникова Е.А./
«____»__________ 20__ г.
Введение
Настоящая работа является составной частью учебно-методического комплекса дисциплины «Математика», специальности 030912 «Право и организация социального обеспечения» по стандартам ФГОС СПО.
Данные методические рекомендации предназначены студентам очной формы обучения для выполнения практических работ в ходе учебных занятий, а так же могут быть использованы для самостоятельного изучения или домашней работы.
Цель методических рекомендаций - помощь студенту в организации учебной практической деятельности и успешном освоении математики.
Методические рекомендации содержат теоретический материал, примеры решения заданий, а так же задачи для самостоятельного выполнения.
В процессе выполнения практических работ у студентов формируются общие и профессиональные компетенции:
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 9. Ориентироваться в условиях постоянного изменения правовой базы.
Практическая работа №1
Тема: Нахождение области определения функции. Выполнение упражнений на вычисление пределов.
Цель: Научиться вычислять пределы функции в точке и на бесконечности.
Ход работы Область определения функции
Под
областью
определения
(существования ) функции
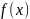понимается совокупность всех действительных
значений аргумента
,
при которых функция определена и
выражается действительным числом.
Пример
1.
Найти область определения функции
Решение.
Очевидно, что при любом действительном
значении
функция
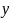также выражается действительным числом.
Следовательно, данная функция определена
при любом значении
.
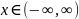Этот результат можно записать в виде
.
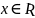Отметим особенности отыскания области определения некоторых функций.
При отыскании области определения дробной функции нужно исключить значения аргумента, при которых знаменатель обращается в нуль.
Пример
2.
Найти область определения функции:
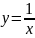
Решение.
Знаменатель обращается в нуль при
.
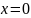Данная функция принимает действительные
значения для всех
,
кроме
.
Следовательно, областью определения
данной функции являются интервалы
.
Пример
3.
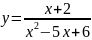
Решение.
Функция определена для всех действительных
значений
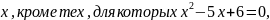т.е
корней квадратного трехчлена
ими являются числа
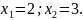Следовательно, функция определена на
интервалах
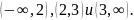
Пример
4.
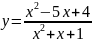
Решение.
Приравняв знаменатель дроби нолю и
решив полученное квадратное уравнение
,
убедимся, что его корни
.
Ни при одном действительном значении
знаменатель в нуль не обращается. Поэтому
данная функция определена при всех
действительных значениях
.
Ее областью определения является
бесконечный интервал
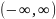
2. Если аналитическое выражение функции содержит корень четной степени, то при отыскании области определения функции нужно исключить значения аргумента, при которых подкоренное выражение принимает отрицательные значения
Пример
5.
Найти области определения функций:
Решение.
Заметим, что эта функция имеет смыл
только в том случае, когда подкоренное
выражение больше нуля либо равно нулю.
Если же подкоренное выражение отрицательно,
то
мнимое число. Следовательно,
Итак, данная функция определена только
в том случае, если
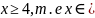
3. Если аналитическое выражение функции содержит логарифм, то при отыскании области существования данной функции нужно исключить значения аргумента, при которых выражение под знаком логарифма принимая отрицательные значения и обращается в нуль.
Пример
6.
Найти области определения функций:
Решение.
Так как выражение под знаком логарифма
должно быть положительно, то
Нельзя смешивать область определения функции с областью значений функции.
Область
значений функции есть множество всех
действительных значений, которые
принимает функция. Например, область
значений функции
есть совокупность всех значений
,
для которых
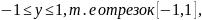а областью определения той же функции
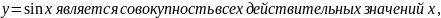т.е промежуток
Задания для самостоятельного решения
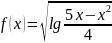Пределы
с неопределенностью вида 
и
метод их решения
Неопределённость
вида
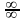- получается при нахождении предела
дроби при
.
Чтобы избавиться от этой неопределённости
нужно числитель и знаменатель поделить
на старшую степень аргумента.
Пример
1
Пример
2
Пример
3
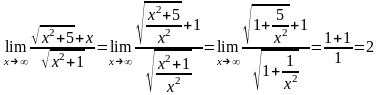
Пределы с неопределенностью вида - ∞и метод их решения
Неопределённость вида ∞ - ∞. – получается при х→∞.
Чтобы избавиться от этой неопределённости выражение стоящее под знаком предела домножают и делят на сопряжённое.
Пример
4
П
ример
5
Пределы
с неопределенностью вида 
и
метод их решения
Неопределённость
- получается при нахождении
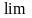дроби при
а) Если дробь рациональная (т.е. в числителе и знаменателе стоят многочлены), то разлагаем числитель и знаменатель на множители и сокращаем критические.
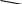
Пример
6
б) Если дробь иррациональная, то домножаем на сопряженное выражение и используем формулу разности квадрата.
Пример
7
