Для расчета цепи методом переменных состояния структуру рис. 2.168 необходимо трансформировать в динамическую структурную схему. Последнее может быть выполнено различными путями. Можно, например,

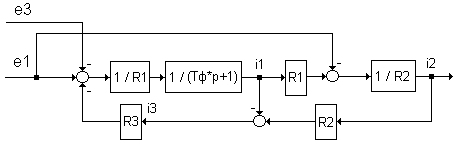
Рис. 2.169

ввести в прямой канал внутреннего замкнутого безынерционного контура последовательно с элементом 1/R₁ апериодическое звено (фильтр) с коэффициентом передачи, равным единице, и малой (фиктивной) постоянной времени T_ф (рис. 2.169). После замены апериодического звена его детализированным эквивалентом может быть легко получена развернутая структурная схема, записаны уравнения состояния и сформирована модель в переменных состояния расчетной структуры.

Другой вариант расчетной структурной схемы цепи (рис.2.170) можно получить путем введения аналогичного фильтра в общую цепь каналов (элемент R₃) обратных связей указанных безынерционных контуров.

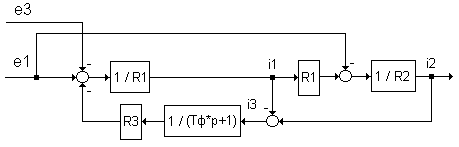
Рис. 2.170

Возможен также вариант расчетной структурной схемы с двумя фильтрами, включенными последовательно в прямые каналы контуров коэффициентами передачи 1/R₁ и 1/R₂ (рис. 2.171).

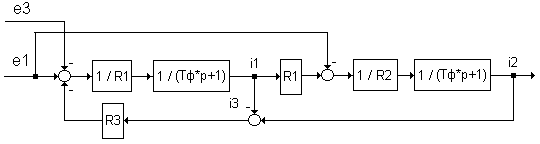
Рис. 2.171

Структуры рис. 2.169, 2.170 и 2.171 эквивалентны с позиции конечного (установившегося) распределения токов в цепи. Разница этих структур проявляется в характере фиктивных переходных процессов в цепи, "порожденных" принятым методом расчета резистивных цепей. Заметим, что определение действительных токов ветвей простых резистивных цепей средствами программных пакетов для анализа динамических цепей может быть также произведено с использованием статической структурной схемы цепи (рис. 2.172), свернутой из схемы рис. 2.168. На схеме рис. 2.172 обозначено: (R₃/R₁)  коэффициент приведения напряжения е₁ к напряжению е₃, R₂/(R₂+R₃)  коэффициент приведения напряжения е₃ к напряжению е₁. Эта схема может быть получена также путем решения исходной системы уравнений рассматриваемой цепи.

Рис. 2.172

Рассмотренный способ преобразования статической структурной схемы в искусственную динамическую при рациональном подборе постоянных времени фильтров оказывается особенно эффективным при исследовании систем, модели которых сводятся к совокупности резистивных и индуктивно (емкостно)-резистивных цепей.

Катушка индуктивности с ферромагнитным сердечником. Общая структура модели катушки индуктивности (рис. 2.173) состоит из двух функциональных блоков, охваченных обратной связью по магнитному потоку.

Р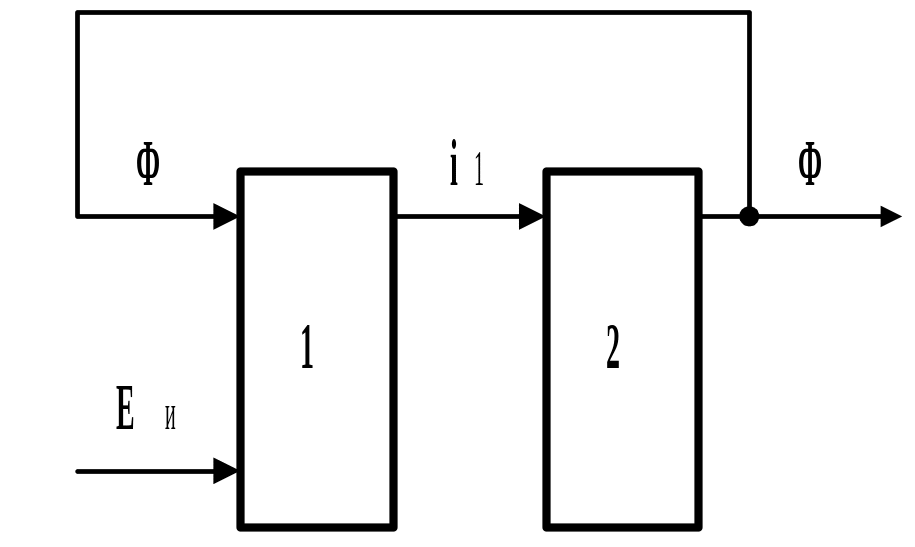 ис. 2.173

Первый блок – модель электрической части катушки, т.е. модель обмотки (входной величиной является ЭДС источника питания, выходной – ток в обмотке; магнитный поток является сигналом обратной связи). Второй блок – модель магнитной системы (входная величина – ток в обмотке, выходная – магнитный поток).

Процессы в обоих блоках имеют тесную связь, поскольку магнитные и электрические явления являются двумя сторонами единого электромагнитного процесса. При этом результаты расчета магнитной цепи используются при определении электродвижущей силы, наводимой в обмотке по закону электромагнитной индукции, а результаты расчета электрической цепи, в свою очередь, оказывают влияние на определение параметров и характеристик магнитной системы а также на протекающие в ней процессы.

Модель катушки индуктивности строится на базе теории цепей; для этого электрическая и магнитная системы представляются в виде их электрической (а) и магнитной (б) схем замещения (рис. 2.174).

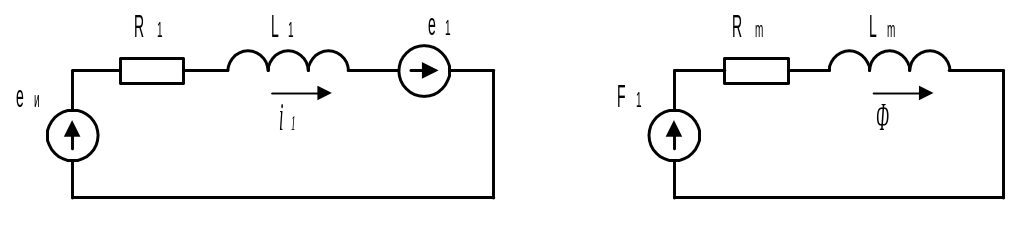а) б)

Рис. 2.174

Для этих схем замещения записываются линейные уравнения электрического и магнитного равновесия, составленные по второму закону Кирхгофа,

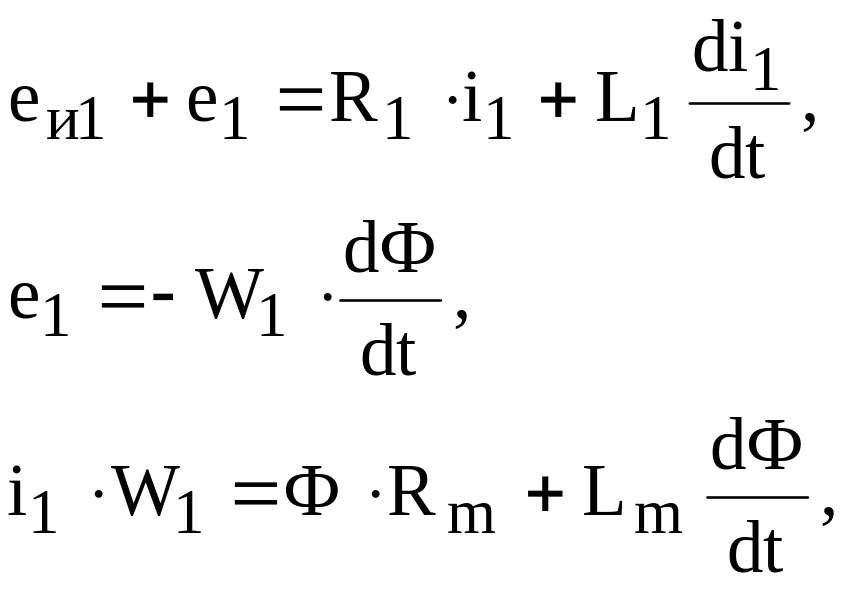(2.59)

где e_и1 – ЭДС источника питания, R₁ и L₁ – активное сопротивление и индуктивность рассеяния катушки, W₁ – число витков, R_m – магнитное сопротивление, L_m – индуктивность магнитной цепи, введенная для учета потерь энергии в сердечнике, Ф – основной поток.

П осле записи системы уравнений в операторной форме при нулевых начальных условиях, нетрудно составить структурную схему модели катушки индуктивности (рис. 2.175).

Р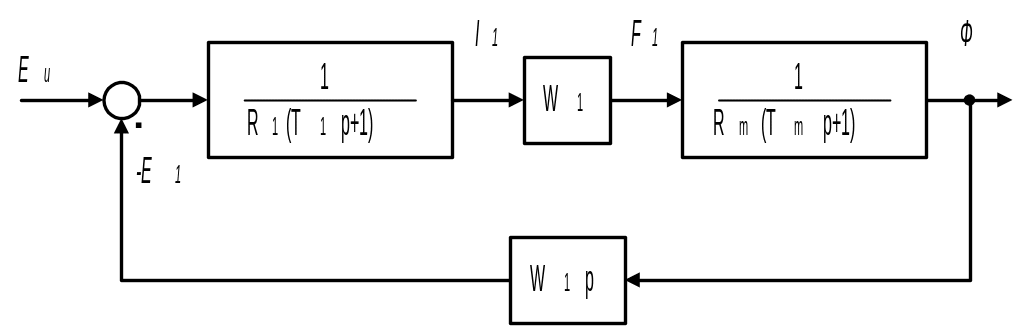 ис. 2.175

Учет нелинейных свойств материала магнитопровода основан на приближенной аналитической аппроксимации зависимости намагниченности вещества от напряженности магнитного поля  = f(H), с ограниченным набором параметров _нач, _max, H_кр (рис. 2.176), причем используемые параметры являются справочными данными, определяющими основные магнитные свойства вещества,

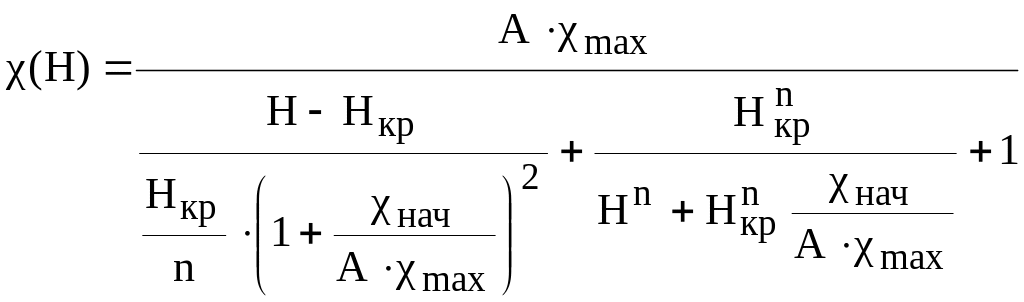(2.60)

г де .

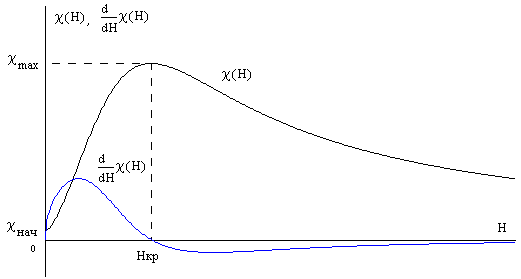
Рис. 2.176

Порядок параболической составляющей функции изменяется в диапазоне от 0,8 до 1,2 и подбирается индивидуально для конкретного магнитного материала. Оптимальное значение n, соответствующее подавляющему большинству применяемых на практике магнитных материалов, равно 1,0.

При этом модель рис. 2.173 оказывается разделенной на линейную (1) и нелинейную (2) части, а третье уравнение в (2.34) становится нелинейным и записывается в виде

,

где , , а и означают длину и сечение сердечника.

Приближенный учет потерь энергии в магнитопроводе основан на использовании в ветвях магнитной схемы замещения магнитной индуктивности L_m, значение которой пропорционально удельным магнитным потерям и зависит от конструкции магнитопровода

, (2.61)

где  коэффициент, учитывающий условия, при которых были определены удельные потери в стали, как то частота f_изм и амплитуда магнитной индукции B_изм; если удельные потери берутся по отношению к массе магнитопровода, то в числителе этого коэффициента учитывается плотность ферромагнитного материала. В первом приближении принимаем эту индуктивность постоянной и соответствующей, например, номинальным значениям f и B.

Формула для определения постоянной времени магнитной цепи T_m=L_m/R_m с учетом (2.36) принимает вид

, (2.62)

т.е. постоянная времени не зависит от геометрических размеров магнитопровода.

При использовании описанной выше методики учета нелинейных свойств ферромагнитных материалов детализированная (алгоритмическая) структурная схема катушки индуктивности примет вид, изображенный на рис. 2.177.

На рис. 2.178 и 2.179 показаны зависимости напряжения, тока и потока катушки от времени при ее включении на источник синусоидальной ЭДС. На рис. 2.180 приведена зависимость потока от тока для данного режима. Можно видеть, что кривые тока и потока несинусоидальны, а выход на предельную петлю гистерезиса происходит за несколько периодов сети.

С ледует отметить, что в ряде случаев оказывается целесообразным искусственно ввести малую индуктивность магнитной цепи. Это позволяет сохранить топологическое соответствие структурной схемы реальной системе, выделить в ней нелинейные части, без преобразования схемы исключить алгебраические контуры.

Р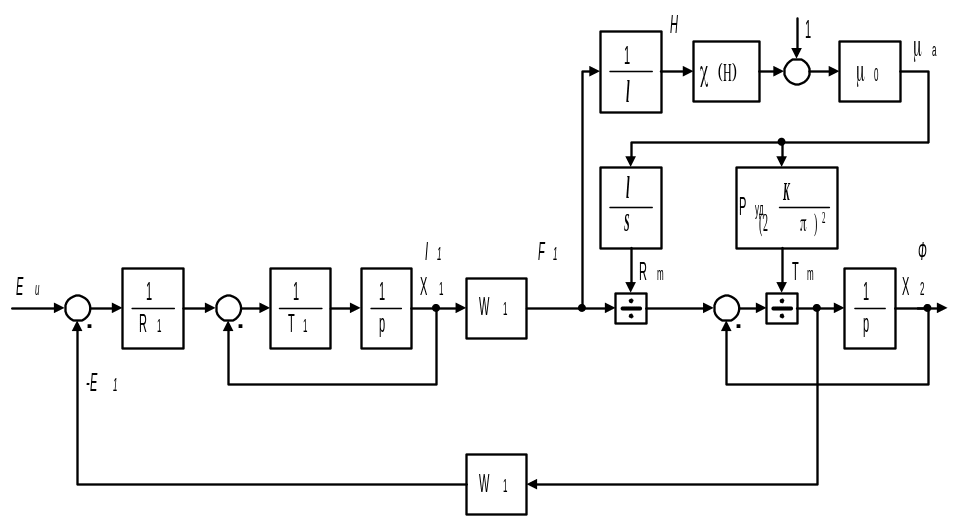 ис. 2.177

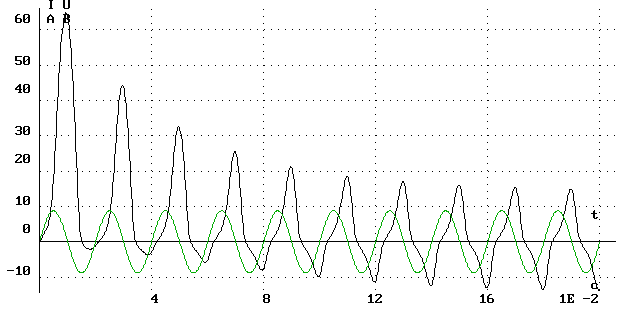
Рис. 2.178

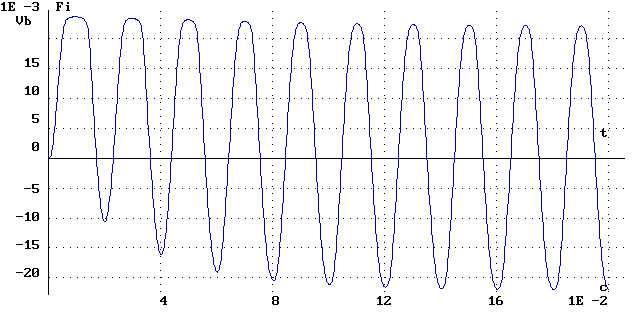
Рис. 2.179

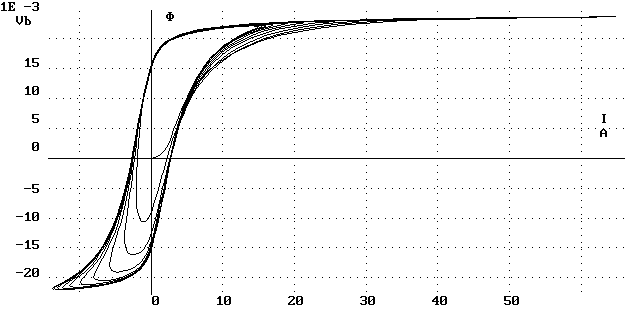
Рис. 2.180

Идеальный трансформатор. Простейший трансформатор состоит из двух индуктивно связанных катушек с индуктивностями L₁ и L₂, расположенных на общем сердечнике, выполненном из ферромагнитного или неферромагнитного материала. Примером трансформатора последнего типа является воздушный (идеальный ) трансформатор. На рис. 2.181 изображена схема такого трансформатора с потерями в активных сопротивлениях первичной R₁ и вторич­ной R₂ катушек (обмоток), нагруженного на R_н L_н.

Рис. 2.181

Для синтеза модели в переменных состояния составим систему дифференциальных уравнений трансформатора для взаимосвязанных контуров I и II в операторной форме при нулевых начальных условиях

u ₁ = R₁(1+pT₁)i₁ + pL₁₂i₂;

e₂ =  pL₂₁i₁ = R₂(1+pT₂)i₂+u₂; (2.63)

u₂= R_н(1+pT_н)i₂,

где T₁=L₁/R₁; T₂=L₂/R₂, T_н=L_н/R_н  электромагнитные постоянные времени.