Контрольные каналы могут быть выполнены в виде структурных модулей, представленных на рис. 2.132.

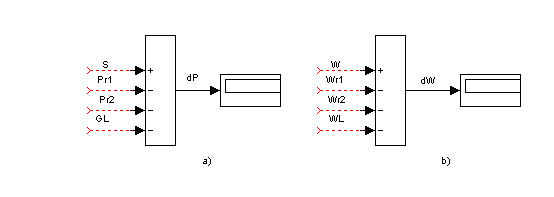
Рис. 2.132

Приняв выходные величины интеграторов в структуре рис. 2.131 за переменные состояния модели (Х₁ = i, Х₂ = W_R1, Х₃ = W_R2, Х₄ = W_L, Х₅ = W), запишем уравнения состояния и уравнения выходов RL-цепи в виде выражений:

dX₁/dt = (e/R  Х₁)R/L; dX₂/dt = Х₁R₁Х₁; dX₃/dt = Х₁R₂Х₁;

dX₄/dt = [(e/R  Х₁)R/L]LХ₁; dX₅/dt = eХ_1;

u_R1 = R₁Х₁; u_R2 = R₂Х₁; u_L = [(e/R  Х₁)R/L]L; (2.31)

P_R1 = u_R1Х₁; P_R2 = u_R2Х₁; G_L = u_LХ₁; S = eХ₁; i = Х₁;

i_в = e/R, i_c = e/R  Х₁.

Для формирования модели цепи по второму способу выполним операцию суммирования напряжений на элементах последовательной RL-цепи, в результате чего имеем уравнение соединения

e = u_R1 + u_R2 + u_L. (2.32)

Уравнения элементов контура

u_R1 = R₁i; u_R2 = R₂i, u_L = Ldi/dt. (2.33)

Если учесть, что d/dt = p тогда

e = u_R1 + u_R2 + u_L,

u_R1 = R₁i; u_R2 = R₂i, u_L = Lpi. (2.34)

Представим (2.34) в виде:

i = u_L (1/L)(1/p); u_L = e  u_R1)  u_R2; (2.35)

u_R1 = R₁i, u_R2 = R₂i.

Уравнениям (2.35) соответствует ДСС двухэлементной RL-цепи, изображенная на рис. 2.133 и отличающаяся от схем рис. 2.129 тем, что в ее узле суммируются напряжения.

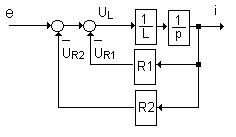
Рис. 2.133

Полная развернутая структура модели RL-цепи с учетом (2.31) показана на рис. 2.134.

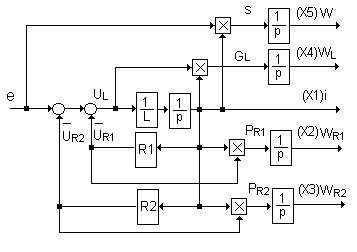
Рис. 2.134

Отметим, что модели рис. 2.131. и 2.134 позволяют проводить анализ динамических процессов в цепях с нулевыми и ненулевыми начальными условиями при воздействиях произвольных источников напряжения. Задание ненулевых начальных условий в известных пакетах (VISIM, SIMULINK и т.п.) обычно производится при редактировании параметров (коэффициент усиления, постоянная времени, начальное значение выходной переменной и т.д.) конкретного блока исследуемой системы. Это может быть выполнено также путем включения на выходы интеграторов дополнительных блоков, суммирующих начальные значения переменных (в данном случае токов) с выходными сигналами интеграторов.

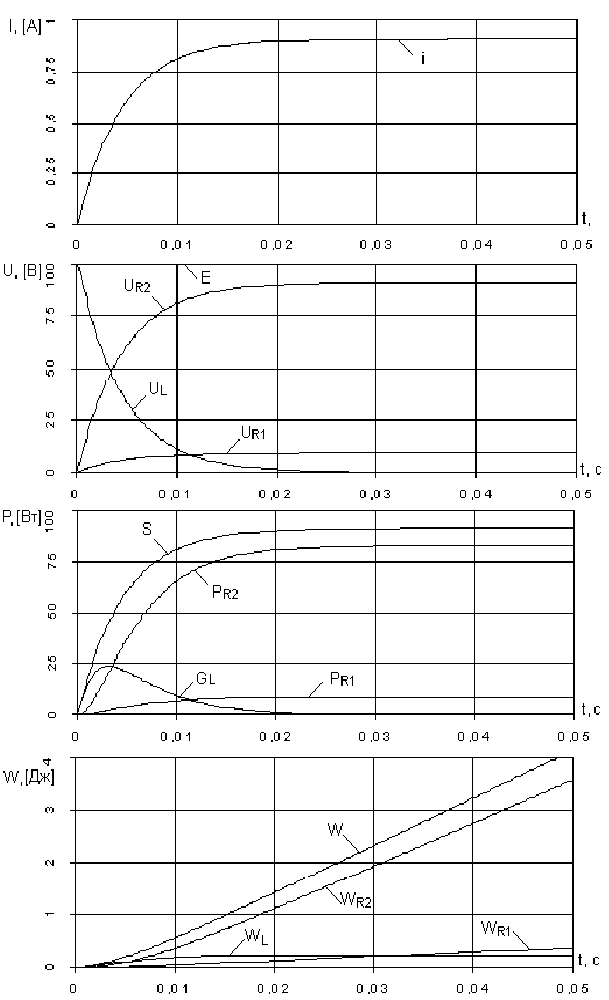
Рис. 2.135

В качестве примера на рис. 2.135 приведены зависимости напряжений, мощностей и энергий на элементах R₁=10 Ом, R₂=100 Ом, L=0,5 Гн от времени при включении цепи на постоянную ЭДС Е=100 В. Там же показаны мощность и энергия источника питания.

П оследовательная трехэлементная RLC – цепь. Для последовательного контура (рис.2.136) с реактивными элементами L и C и активным

Рис. 2.136

сопротивлением R, характеризующим потери в контуре, сформируем интегро-дифференциальное уравнение

e = Ri + Ldi/dt +1/Сidt, (2.36)

где e = e(t) – напряжение на зажимах цепи. Выражение (2.36) запишем в виде:

e = u_R + u_L + u_C, (2.37)

где u_R = Ri, u_L = Ldi/dt, u_C = 1/Сidt.

Если обозначить dt = 1/p и учесть, что d/dt = p, тогда для переменных u_C и u_L получим

u_C = (1/С) (1/p)i, u_L = Lpi. (2.38)

Из выражения u_L = Lpi, имеем

i = u_L /Lp. (2.39)

Используя выражение (2.39) и учитывая, что u_L = e - u_R - u_C, а u_R = Ri и u_C = (1/Сp)i формируется детализированная структурная схема RLC –цепи (рис. 2.137).

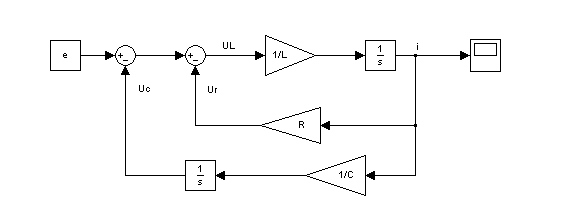
Рис.2.137

На рис. 2.138 изображена полная развернутая структура модели рассматриваемой цепи с учетом каналов измерения мгновенных значений напряжения, мощности и энергии элементов контура.

Рис. 2.138

В качестве примера на рис. 2.139 приведены зависимости напряжений, мощностей и энергий на элементах цепи R=25 Ом, L=0,2 Гн, C=50 мкФ от времени при включении ее на синусоидальную ЭДС е =100 sin (314t).

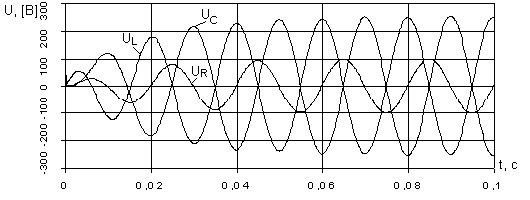
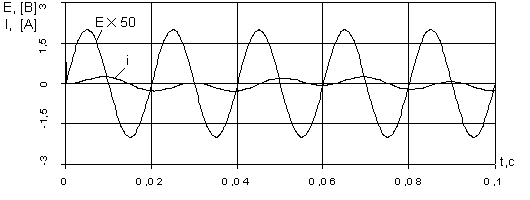
Р ис. 2.139

На рис. 2.140 блоки измерения мощности и энергии представлены в виде подсистем (S-моделей).

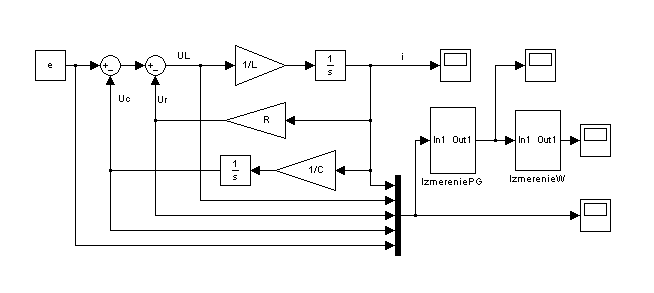
Рис.2.140