2.1.3.3 Исследование модели в частотной и временной области

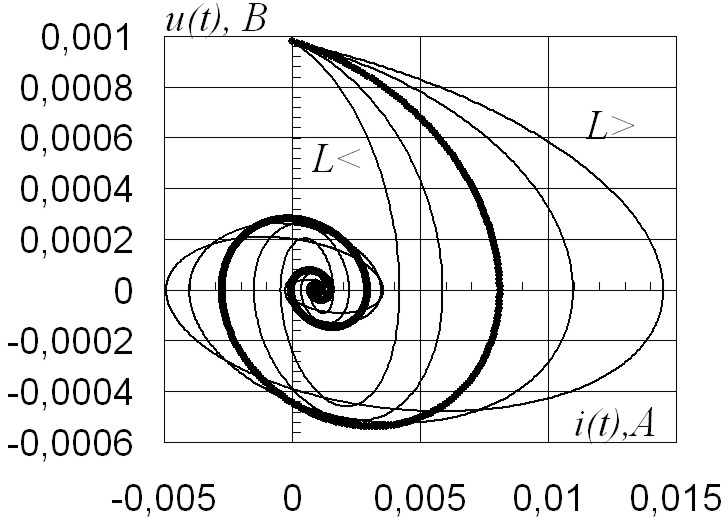
Для изучения и графической интерпретации поведения переменных состояния выполняют моделирование режима цепи по фазовым траекториям в соответствии с выражениями

, .

	Рис. 2.69

Для этого применяют специальный прием, связанный с использованием схемотехнических моделей, например с источником напряжения, управляемым током (ИНУТ) показана на рис. 2.69.

Для диагностики тока в ветви устанавливают источник напряжения, управляемый током (ИНУТ). Коэффициенты передачи управляемых источников ЭДС k равны единице u(t) = k i(t) = i(t).

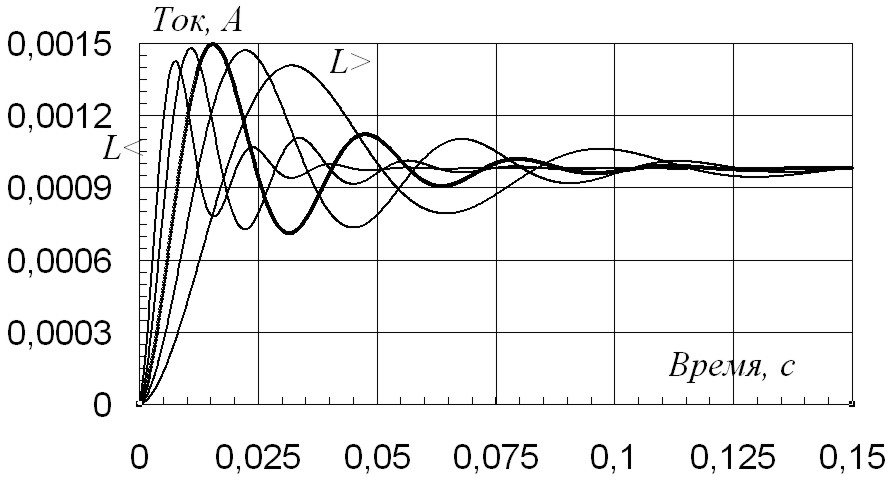
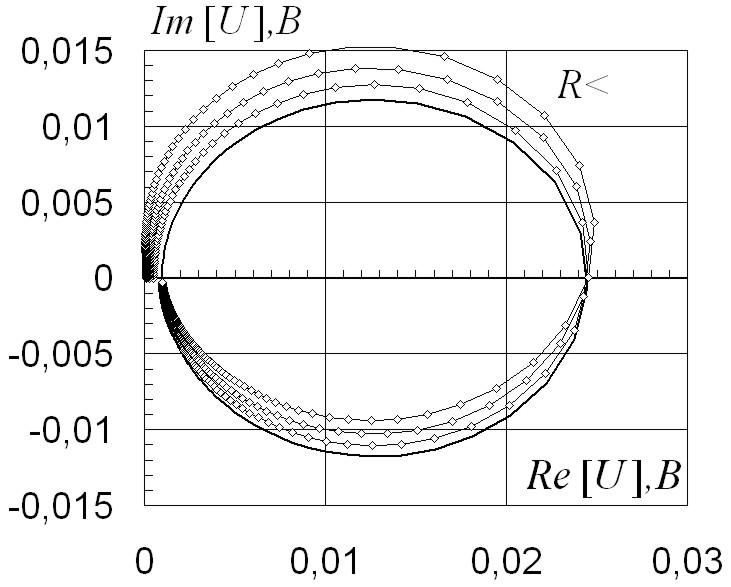
Семейство фазовых траекторий переменных состояния на плоскости получено схемотехническим моделированием при изменении индуктивности. Семейство фазовых траекторий u_C(t) = i_C(t) для емкостного элемента представлено на рис. 2.70. На рис. 2.71 i_L(t) = u_L(t) – для индуктивного, при выборе значений L по закону L _j = (2)^k L_i, с коэффициентом в степени k =  1.

	Рис. 2.70			Рис. 2.71

Жирной линией выделена фазовая кривая для исходных параметров системы. Соответствующие динамические характеристики u_C(t), i_L(t) для исходных значений элементов цепи показаны на рис. 2.72, 2.73.

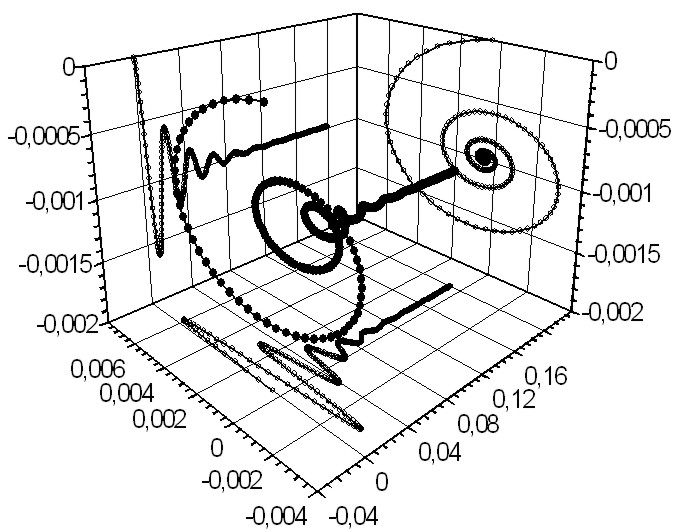
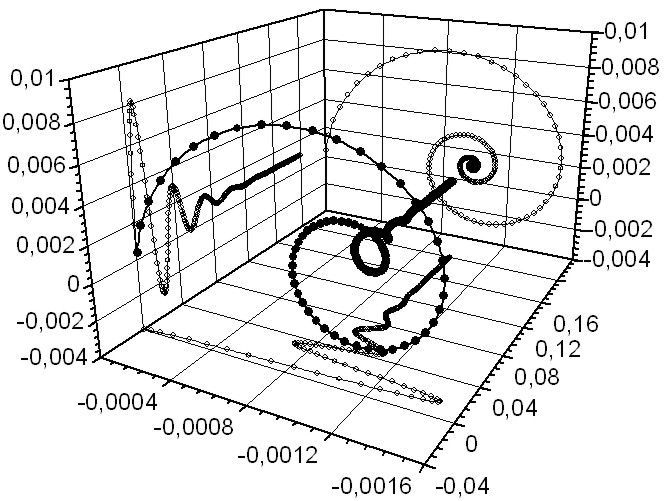
Семейство фазовых траекторий в пространстве состояний получено схемотехническим моделированием при изменении регулируемых параметров ARC-прототипа. Фазовая траектория и фазовые портреты переменных состояния (измерены напряжения на конденсаторах) в переходном процессе (APPC). При расчетном значении R₄, получены фазовые траектории, показанные на рис. 2.72. При фиксированном значении регулировочного резистора R₄ в сторону уменьшения наблюдаются аналогичные процессы (рис. 2.73), сопровождающиеся увеличением длительности.

Проекции пространственных фазовых траекторий на плоскости соответствуют двум динамическим кривым переменных состояния и фазовому портрету на плоскость переменных состояния при поочередном обнулении значений соответствующих производных.

	Рис. 2.72			Рис. 2.73

Фазовые траектории, показанные на рис. 2.75, соответствуют регулировочному состоянию между соседними динамическими характеристиками на одном шаге регулирования. Они описывают переход системы из одного установившегося состояния в другое в динамике регулирования.

	Рис. 2.74			Рис. 72.5

Рассмотренные кривые получены для регулирования R₂ с шагом 1-2-4-8.

	Рис. 2.76

Регистрация переменой состояния и ее производной выполнена при функциональной настройке звена как показано на рис. 2.76. Характер регулирования нелинейный, при наличии колебательной подстройки в пределах допуска.

Аналогичные кривые можно получить для RLC-цепи прототипа, учитывая возможности изменения коэффициентов в уравнениях УПС.

	Рис. 2.77			Рис. 2.78

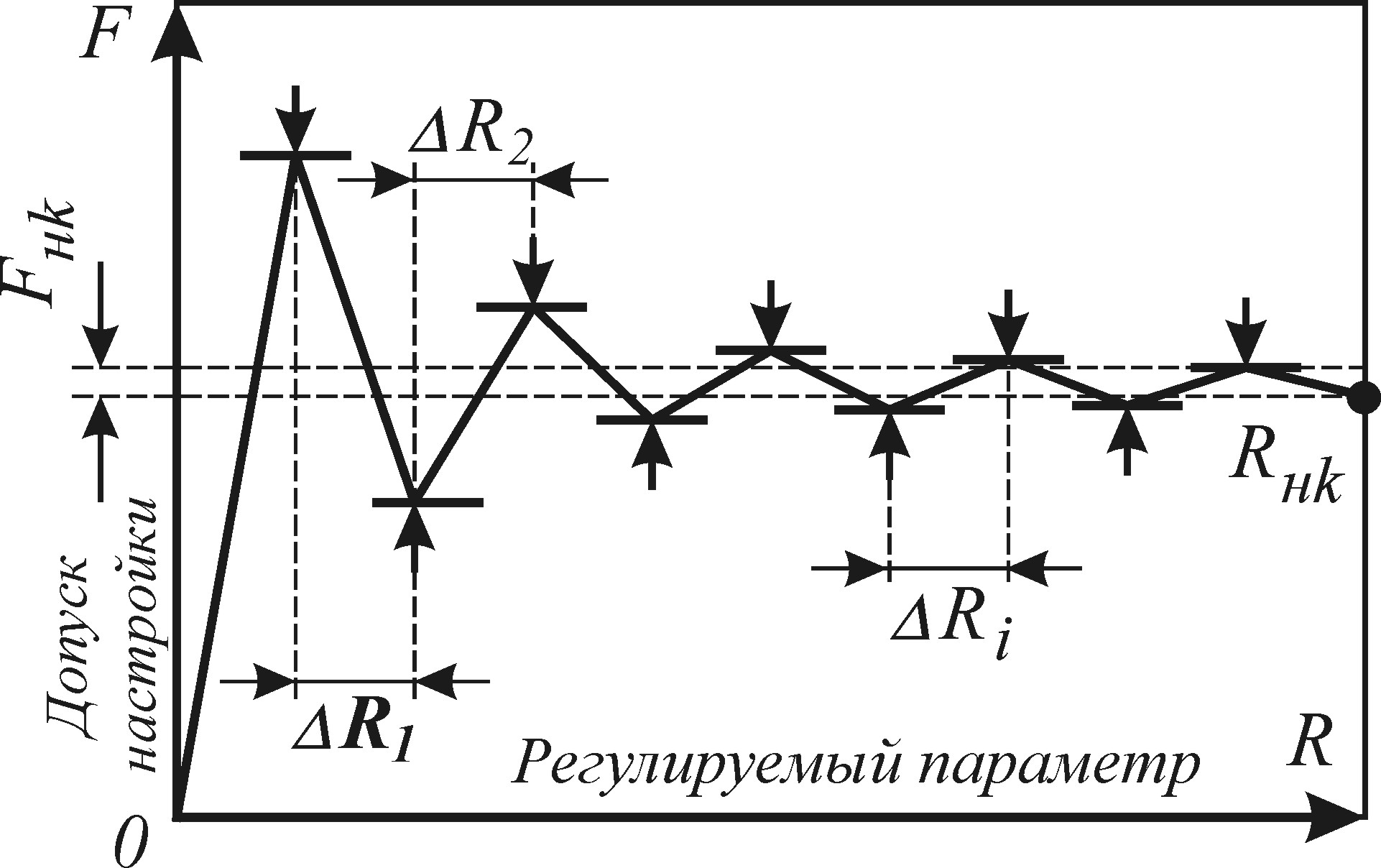
При построения графиков использовано до 1500 точек на каждую кривую. В результате расчета и моделирования получены семейства регулировочных характеристик (рис. 2.79 – 2.95) при изменении различных параметров модели (рис. 2.66). Меняя коэффициенты в уравнениях динамической системы по расчетным формулам для модели получают значения элементов R_i. Настройкой элементов поведение модели может быть скорректировано с учетом справочных характеристик, приведенных ниже.

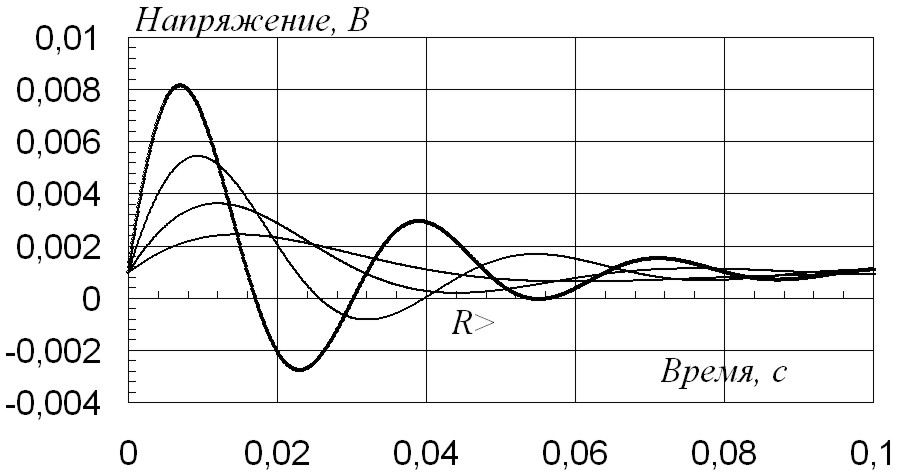
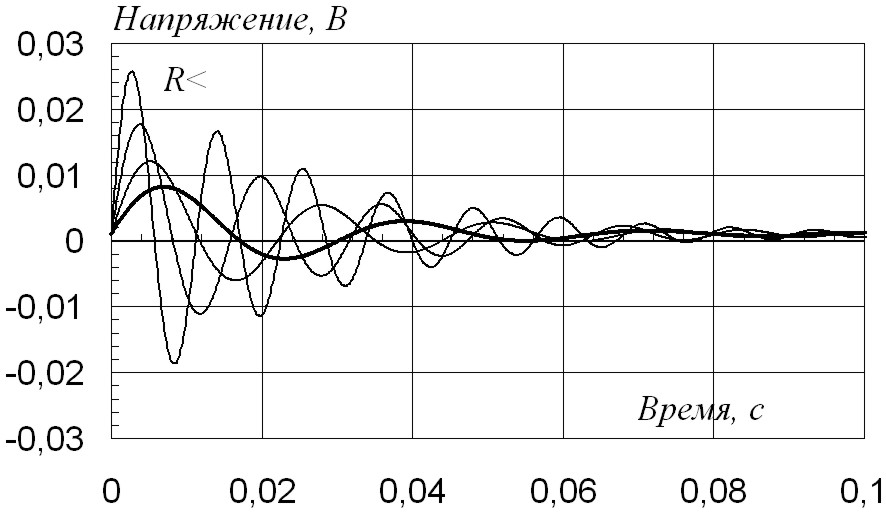
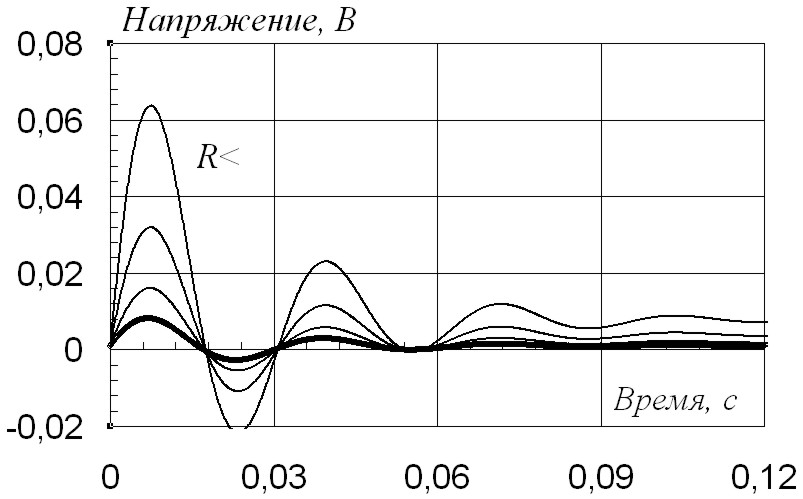
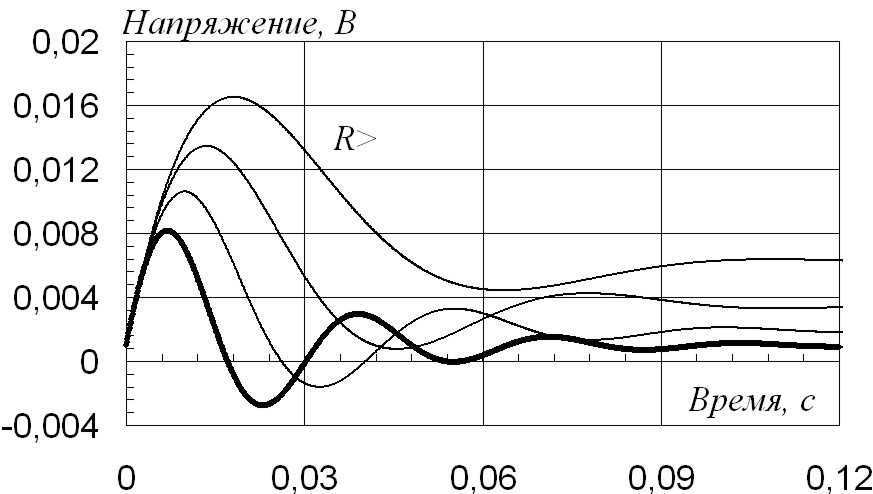
Динамические кривые системы при регулировании резистора R₄ инвертора напряжения представлены на рис. 2.79, 2.80. Закон изменения регулируемого параметра R _j = (2)^k R_i, с коэффициентом в степени k=1. Жирной линией выделена кривая для исходных параметров системы.

	Рис. 2.79			Рис. 2.80

Слева расположены кривые, полученные в соотвтетсвии с обозначенной закономерностью при увеличении резистора в 1–2–4–8 раз, справа – при уменьшении в 0,125–0,25–0,5–1 раз.

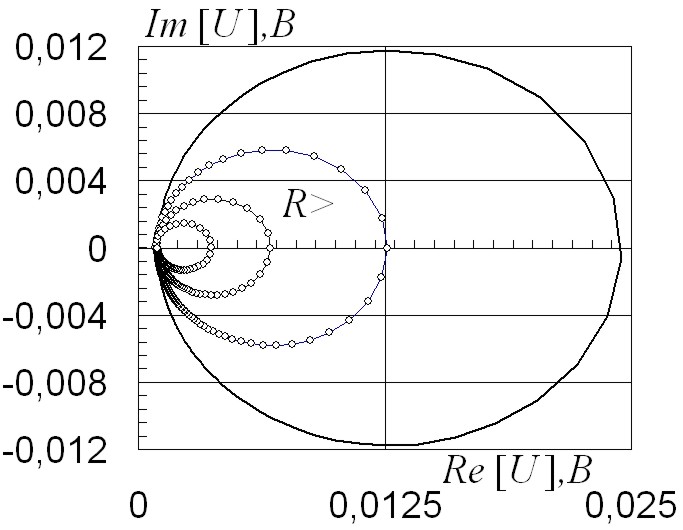
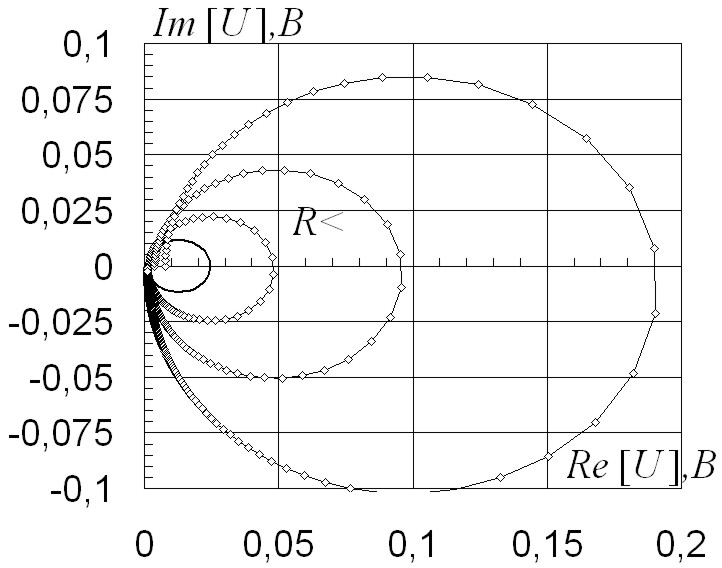
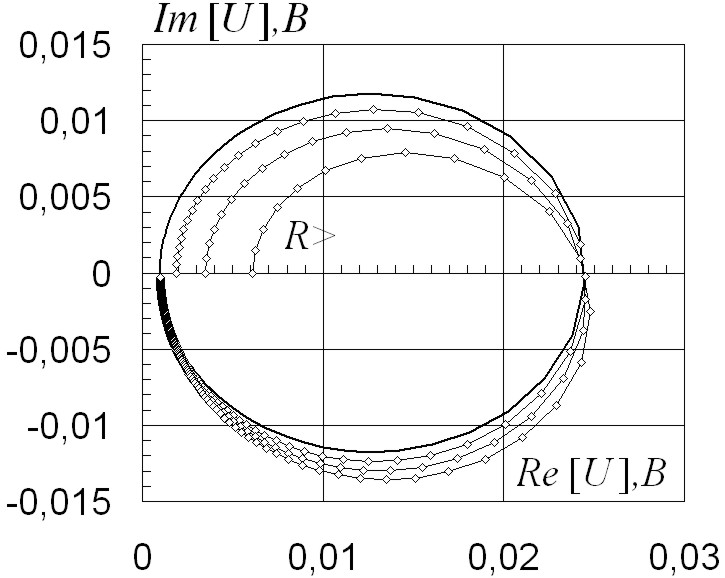
Построение частотных характеристик (рис. 2.81, 2.82), соответствующих регулировочным кривым также выполняют при изменении регулируемого параметра в обе стороны. Используют режим частотного анализа для комплексных частотных характеристик цепи.

	Рис. 2.81			Рис. 2.82

Характеристики получены наложением диаграмм в офисном приложении MS Excel. Сплошной линией изображена кривая для исходных параметров цепи. Переходные характеристики при регулировании резистора R₁ представлены на рис. 2.83, 2.84.

	Рис. 2.83			Рис. 2.84

Соответствующие комплексные частотные характеристики при регулировании R₁ показаны на рис. 2.85, 2.86.

	Рис. 2.85			Рис. 2.86

Чередование характеристик на комплексной плоскости зависит от порядка нумерации узлов электрической цепи.

Переходные характеристики при регулировании резистора R₂ представлены на рис. 2.87, 2.88. Изменение номинала резистора соответственно изменяет длительность переходного процесса.

	Рис. 2.87			Рис. 2.88

Фазовые траектории и портреты (рис. 2.89) получены измерением напряжений в узлах цепи, присоединенных к емкостям. Для выходного напряжения на конденсаторах C₁, C₂ (аналог переменных состояния) получены фазовые кривые связанных между собой напряжений. Фазовые траектории показанные на рис. 2.90 соответствуют регулировочному состоянию между соседними динамическими характеристиками на одном шаге регулирования. Они описывают переход системы из одного установившегося состояния к другое в динамике регулирования по линейному закону.

Соответствующие комплексные частотные характеристики при шаговом регулировании R₂ показаны на рис. 2.91, 2.92.

	Рис. 2.91			Рис. 2.92

Переходные характеристики при регулировании резистора R₃ представлены на рис. 2.93, 2.94. Изменение номинала резистора соответственно изменяет апериодическую составляющую, не меняя частоты периодической.

	Рис. 2.93			Рис. 2.94

Переходные характеристики при регулировании резистора R₁₀ представлены на рис. 2.95, 2.96. Регулирование номинала резистора изменяет постоянную составляющую переходного процесса.

	Рис. 2.95			Рис. 2.96

Соответствующие комплексные частотные характеристики при регулировании резистора R₁₀ показаны на рис. 2.97, 2.98.

	Рис. 2.97			Рис. 2.98

Для рассчитанных параметров системы переходные характеристики при регулировании резистора R₈ совпадают с кривыми, полученными при настройке системы элементом R₁₀.

Исследование возможностей регулирования качества переходного процесса в ARC-прототипе выполняют с учетом ограничения по устойчивости. При этом по методу расширенных узловых уравнений формируют математическую модель, получают передаточную функцию по напряжению и исследуют ее на устойчивость.

При исследовании динамической системы по схемотехнической модели изменения динамики системы вплоть до нарушения устойчивости достигают пошаговым изменением R (эквивалент подстроечных резисторов), при этом изменяются нули и полюсы передаточной функции.

	Рис. 2.99

На рис. 2.99 показана поверхность, образованная кривыми переходного напряжения на емкостном элементе в осях координат u(t), t, k.

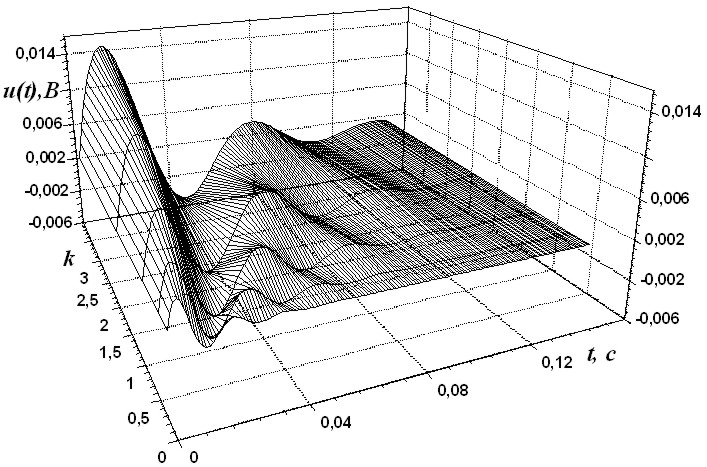
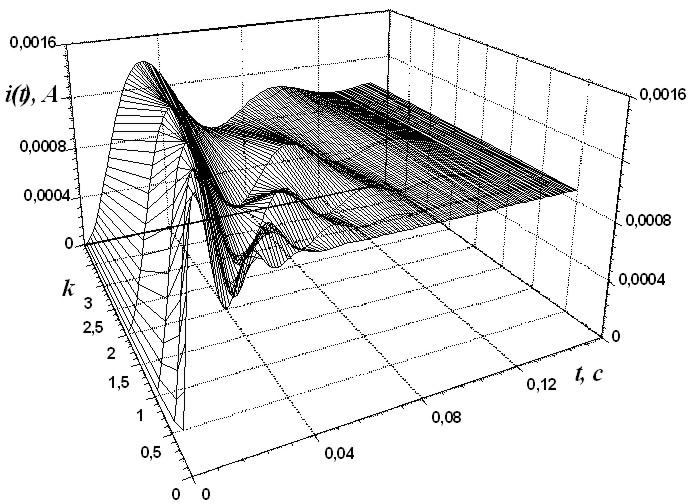
На рис. 2.100 изображена поверхность, образованная кривыми переходного тока индуктивного элемента в осях координат i(t), t, k. Построение объемных характеристик переходного режима улучшает наглядность изображения регулировочных возможностей. Это представляется существенным при настройке моделей систем автоматического управления. Приведенные семейства характеристик соответствуют фазовым портретам переменных состояния (рис. 2.72, 2.73) в области устойчивого состояния ARC-цепи.

	Рис. 2.100

Применение рассмотренной методологии, средств и способов моделирования цепей при изучении их динамики позволяет провести исследование в сжатые сроки. При этом основным инструментом машинного моделирования режимов выступает комплекс программных средств. Особенностью предлагаемого подхода является отсутствие явно выраженного упора на некую универсальную среду машинного моделирования. Предполагается, что постановка задачи машинного моделирования предполагает, по мнению авторов, безусловное овладение фундаментальными вычислительными методами и алгоритмами. А изучение непрерывно совершенствуемых интерфейса и технологий моделирования в различных программных средах предполагается изучать за пределами изложенных вопросов.

Некоторые навыки исследования могут быть получены с применением программно-методического комплекса теории цепей, использованного в ходе реализации примеров. Кроме линейных систем существуют возможности моделирования нелинейных и параметрических систем. Однако применение вычислительных методов здесь существенно сложнее и требует углубленного изучения особенностей соответствующих математических и схемных моделей цепи. Цепи с переменными параметрами реализуются посредством применения технических решений импульсной и ключевой схемотехники. Для нелинейных цепей применимы различные типы анализа при использовании реальных вольтамперных, вебер-амперных и кулон-вольтных характеристик элементов.