6. Неравенства и системы неравенств

Теорема 1. Если какой-либо член неравенства с одной переменной перенести из одной части неравенства в другую с противоположным знаком, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному. Теорема 2. Если обе части неравенства с одной переменной умножить или разделить на одно и то же положительное число, оставив при этом без изменения знак неравенства, то получится неравенство, равносильное данному. Теорема 3. Если обе части неравенства с одной переменной умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится неравенство, равносильное данному. Линейным называется неравенство вида ax+b>0 (соответственно ax+b<0, ax+b³0, ax+b£0), где а и b – действительные числа, причем а¹0. Решение этих неравенств основано на трех теоремах равносильности изложенных выше. Пример Решить неравенство: . Освободимся от знаменателей, для чего умножим обе части неравенства на положительное число 6, оставив без изменения знак неравенства. , далее последовательно получаем ; . Последнее неравенство верно при любом значении х, так как при любом значении переменной х получается истинное высказывание 0>-55. Поэтому множеством его решений служит вся числовая прямая.

Система неравенств.

Пример 1. Решить систему неравенств:     

	x

                  

С помощью числовой прямой находим, что пересечением этих множеств служит интервал . Это и есть множество решений данной системы.

Неравенства и системы неравенств с одной переменной второй степени

Неравенства вида , , , , где – заданные числа, причем , называются квадратными неравенствами или неравенствами второй степени. Основной метод решения таких неравенств – метод интервалов. Если дискриминант квадратного уравнения положительный, то квадратный трехчлен можно разложить на множители , где , и проверить знак выражения в промежутках, на которые разбивают действительную ось найденные значения корней. Если дискриминант квадратного уравнения отрицательный, то квадратный трехчлен не меняет знак ни при каких действительных значениях переменной. Если и , то для всех . Если и , то для всех . Если дискриминант квадратного трехчлена равен нулю, то выражение представляет собой полный квадрат и, в зависимости от знака , принимает либо только неотрицательные, либо только неположительные значения.

Пример. Решить неравенство .

Решение. Найдем корни квадратного трехчлена: 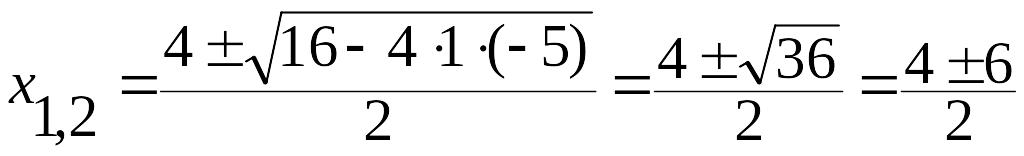, , . Неравенство можно записать в виде . Обозначим на числовой оси точки , и проверим знак выражения в промежутках, на которые разбивают действительную ось найденные значения корней. Если , то ; если , то ; если , то . Поэтому решением неравенства будут значения переменной .

Ответ: .

Пример. Решить неравенство .

Решение. Найдем дискриминант квадратного трехчлена: . Поскольку , , то квадратный трехчлен положителен при всех действительных значениях переменной .

Ответ: .

Пример. Решить неравенство .

Решение. Найдем дискриминант квадратного трехчлена: . Поскольку , , то квадратный трехчлен отрицателен при всех действительных значениях переменной , то есть выражение всегда меньше нуля, а исходное неравенство не имеет решений.

Ответ: неравенство не имеет решений.

Пример. Решить неравенство .

Решение. Второй из сомножителей в приведенном неравенстве не является линейным. Поэтому разложим выражение на множители: . Перепишем исходное неравенство в виде . Отметим на действительной оси корни многочлена , то есть те значения переменной , при которых сомножители обращаются в нуль: , , , . В интервалах , , , , определим знак многочлена , подставляя вместо переменной произвольные значения из интервалов. Решением неравенства будут те интервалы, в которых выражение принимает положительные значения

7. Многочлены. Формулы сокращенного умножения

Разность квадратов Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.

a² - b² = (a - b)(a + b)

Примеры:

• 15² - 2² = (15 - 2)(15 + 2) = 13 x 17 = 221

• 9a² - 4b²с² = (3a - 2bc)(3a + 2bc)

Квадрат суммы Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа плюс квадрат второго числа.

(a + b)² = a² + 2ab + b²

• (8a + с)² = 64a² + 16ac + c²

Квадрат разности Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.

(a - b)² = a² - 2ab + b²

(a - b)² = (b - a)²

Куб суммы Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.

(a + b)³ = a³ + 3a²b + 3ab² + b³

Куб разности Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.

(a - b)³ = a³ - 3a²b + 3ab² - b³

Сумма кубов Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.

a³ + b³ = (a + b)(a² - ab + b²)

Разность кубов Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.

a³ - b³ = (a - b)(a² + ab + b²)