
- •Отчет по лабораторной работе №1
- •Постановка задачи:
- •Аналитическое решение
- •Метод конечных разностей (явная схема)
- •Метод конечных разностей (неявная схема)
- •Регулярный режим охлаждения
- •Результаты расчетов Сравнение численных решений с аналитическим
- •Зависимости температуры по сечению
- •Темп охлаждения
- •1 Метод.
- •2 Метод.
- •3 Метод (графический).
- •Кривые охлаждения
- •Аналитический метод
- •Мкр явная схема
- •Мкр неявная схема
Темп охлаждения
Число Био:

Определим координату точки А.




1 Метод.
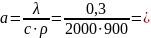
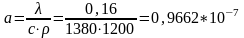 м2/с
м2/с
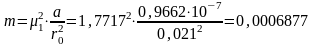 1/с
1/с -
темп охлаждения
-
темп охлаждения
2 Метод.

 - коэффициент
неравномерности распределения температуры
в теле
- коэффициент
неравномерности распределения температуры
в теле
 - модифицированное
число Био
- модифицированное
число Био


 -
к-т формы тела
-
к-т формы тела
 -площадь
поверхности на единицу длины
-площадь
поверхности на единицу длины
 -
объем цилиндра на единицу длины
-
объем цилиндра на единицу длины

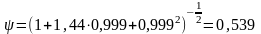



3 Метод (графический).
τ, с |
Lnυ (на оси) |
Lnυ (на границе) |
0 |
4,403 |
4,278 |
320 |
4,367 |
3,618 |
640 |
4,253 |
3,319 |
960 |
4,071 |
3,079 |
1280 |
3,868 |
2,856 |
1600 |
3,625 |
2,596 |
1920 |
3,445 |
2,426 |
2240 |
3,233 |
2,213 |
2560 |
3,02 |
2 |
2880 |
2,806 |
1,787 |
3200 |
2,526 |
1.494 |
 - время
выхода на регулярный режим
- время
выхода на регулярный режим
 (1/с)
(1/с)
Кривые охлаждения
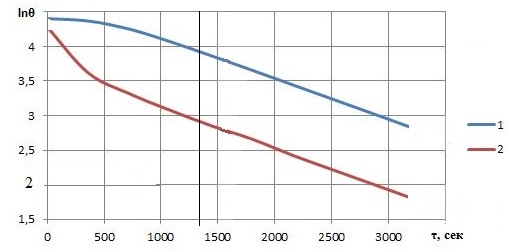
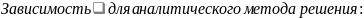 1-для точек на оси
цилиндра; 2-на поверхности
1-для точек на оси
цилиндра; 2-на поверхности

 р
р
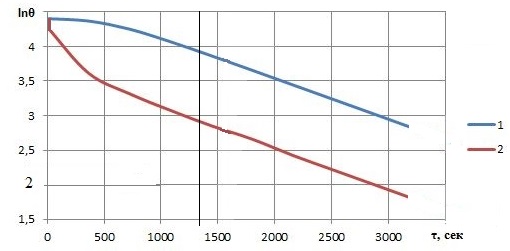
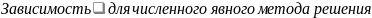 :
1-для точек на оси цилиндра;
2-на поверхности
:
1-для точек на оси цилиндра;
2-на поверхности
р
 :
1-для точек на оси цилиндра;
2-на поверхности
:
1-для точек на оси цилиндра;
2-на поверхности
Расчетные программы:
Аналитический метод
program analit;
const
r0=0.021; t0=95; tcp=15; alpha=22;lamda=0.16;c=1380;p=1200;
a=lamda/(c*p);Bi=(alpha*r0)/lamda;
type mass=array[0..19]of real;
type mass2=array[1..6] of real;
var F,G,T,r:real;
i,j,tau:integer;
S,S1,x,y:real;
J0,J1:mass;
M:mass2;
function fact(i:integer):real;
begin
F:=1; G:=1;
while G<=i do begin
F:=F*G;
G:=G+1;
end;
fact:=F;
end;
// Функция Бесселя J0
function Bessel0(M:real):real;
begin
S:=0;
for i:=0 to 19 do begin
J0[i]:=-exp(ln((M*M)/4)*i)/(fact(i)*fact(i));
if i mod 2 = 0 then J0[i]:=J0[i]*(-1); end;
for i:=0 to 19 do
S:=(S+J0[i]);
bessel0:=S;
end;
// Функция Бесселя J1
function Bessel1(M:real):real;
begin
S1:=0;
for i:=0 to 19 do begin
J1[i]:=-exp(ln((M*M)/4)*i)/(fact(i)*fact(i+1));
if i mod 2 = 0 then J1[i]:=J1[i]*(-1); end;
for i:=0 to 19 do
S1:=S1+J1[i];
S1:=(M/2)*S1;
bessel1:=S1;
end;
// Корни уравнения
begin
for j:=1 to 6 do begin
if j=1 then begin y:=0; x:=3.14; end;
if j=2 then begin y:=3.14; x:=6.28; end;
if j=3 then begin y:=6.28; x:=9.42; end;
if j=4 then begin y:=9.42; x:=12.56; end;
if j=5 then begin y:=12.56; x:=15.7; end;
if j=6 then begin y:=15.7; x:=18.84; end;
repeat
begin
S:=0; S1:=0;
M[j]:=(y+x)/2;
for i:=0 to 19 do
begin
J0[i]:=-exp(ln((sqr(M[j]))/4)*i)/(fact(i)*fact(i));
if i mod 2 = 0 then J0[i]:=J0[i]*(-1);
end;
for i:=0 to 19 do
S:=(S+J0[i]);
for i:=0 to 19 do
begin
J1[i]:=(-exp(ln((sqr(M[j]))/4)*i)/(fact(i)*fact(i+1)));
if i mod 2 = 0 then J1[i]:=J1[i]*(-1);
end;
for i:=0 to 19 do
S1:=S1+J1[i];
S1:=(M[j]/2)*S1;
if (S/S1) > (M[j]/bi) then y:=M[j]
else if (S/S1) < (M[j]/bi) then x:=M[j];
end;
until abs((S/S1)-(M[j]/bi))<0.00000001;
writeln(M[j]:0:4);
end;
// Аналитическое решение
repeat
T:=0;
r:=0.00000000000000000000001;
while r<0.022 do
begin
T:=0;
for j:=1 to 6 do
T:=T+(2*(t0-tcp)*bessel1(M[j])/(M[j]*(sqr(bessel0(M[j]))+sqr(bessel1(M[j])))))*bessel0(M[j]*r/r0)*exp(-(M[j]*M[j])*a*tau/(r0*r0));
if (tau=0) or (tau=32) or (tau=1600) or (tau=3200) then
writeln(tau,' ',r:6:4,' ',(T+tcp):6:3);
r:=r+0.001;
end;
tau:=tau+32;
until tau>3200
end.
