Министерство образования и науки Российской Федерации

Пермский национальный исследовательский политехнический университет

Кафедра «Конструирования и технологий в электротехнике»

Отчет по лабораторной работе №1

Тема: Нестационарные процессы теплопроводности.

Охлаждение бесконечного цилиндра

Вариант №7

Выполнил: ст-т гр. КТЭИ-10 Гущин А.В.

Принял: профессор Щербинин А.Г.

Пермь 2013

Исходные данные:

Материал - ПВХ;

r₀= 0.023 м;  = 21 Вт/(м²•  C); t₀= 95  C; t_ж = 15  C; _к = 3600 c; =1300 кг/м³;

=0,17 Вт/(м²С); с=1300 Дж/(кгС)

Постановка задачи:

1. Решить задачу аналитически. Решить задачу методом конечных разностей по явной и неявной схеме. Провести сравнение с аналитическим решением.

2. По числу Био определить координату точки А на оси абсцисс, через которые для любого момента времени проходят касательные к кривым на поверхности.

3. Определить темп охлаждения для регулярного режима охлаждения тремя способами.

Аналитическое решение

Цилиндр радиусом r_о отдает тепло окружающей среде через свою боковую поверхность; коэффициент теплоотдачи α во всех точках поверхности одинаков и остается постоянным на протяжении всего периода охлаждения. Температура среды t_ж постоянна. Начальное распределение температуры задано: t(r,0)=t₀. Отсчет температуры цилиндра будем вести, как и в предыдущем разделе, от температуры окружающей среды . Требуется найти распределение температуры внутри цилиндра.

При этих условиях уравнение теплопроводности принимает вид:

. (2)

Граничные и начальные условия:

при τ = 0 и 0 ≤ r ≤ r_o ;

при τ > 0 и r = 0 ;

при τ > 0 и r = r_о .

Решением дифференциального уравнения (2) является:

, (3)

где J_о, J₁ – функции Бесселя первого рода нулевого и первого порядка; - корни характеристического уравнения

; (4)

- безразмерное число Био. Функции Бесселя первого рода n-го порядка (n=0,1,2,..) может вычисляться разложением в ряд:

. (5)

При вычислении функции Бесселя по формуле (5) число членов ряда задать равным 20.

Метод конечных разностей (явная схема)

.

Граничные и начальные условия:

при τ = 0 и 0 ≤ r ≤ r_o ;

при τ > 0 и r = 0 ;

при τ > 0 и r = r_о .

; ;

N: ; ; i=0,1,2,…N;

M: ; ; j=0,1,2,…M;

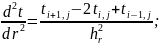
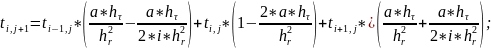
Метод конечных разностей (неявная схема)

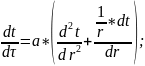
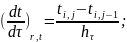
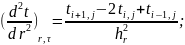
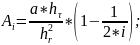
Поскольку разностная схема не позволяет сразу определить неизвестные, то она называется неявной. Определение температуры в j слое для узлов i производится решением системы N-1 линейного алгебраического уравнения с N-1 одной неизвестной температурой.

Задача решается методом прогонки.

П рименяется для частного случая разряжённых трёхдиагональных матриц

Последующее значение вычисляется из предыдущего

Регулярный режим охлаждения

Если безразмерное время (число Фурье ) больше 0,3, то процесс охлаждения из неупорядоченной стадии переходит в стадию регулярного режима.

При регулярном режиме охлаждения изменение температурного поля рассматриваемого тела во времени принимает простой и универсальный вид

, (6)

Тогда

. (7)

Из уравнения (7) следует, что натуральный логарифм избыточной температуры для всех точек тела изменяется во времени по линейному закону.

Величина m, 1/с, есть положительное число, не зависящее от координат и времени. Эта величина характеризует интенсивность охлаждения (нагревания) тела и называется темпом охлаждения (нагревания).

Темп охлаждения однородного тела при конечном значении коэффициента теплоотдачи пропорционален коэффициенту теплоотдачи и внешней поверхности тела и обратно пропорционален полной теплоемкости тела :

, (8)

здесь – коэффициент неравномерности распределения температуры в теле и зависит от условий охлаждения на поверхности тела, .

Величина определяется по формуле

, (9)

где 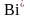– модифицированное число Био.

, (10)

где – коэффициент формы.

Для тел простой формы величина определяются по аналитическим формулам

для цилиндра длиной

;