3. Вирази зі змінною. Область визначення виразу
Означення.
Якщо записи складаються
з чисел, знаків дій і букв, замість яких
можна підставляти числа, то вони
називаються виразами зі змінною. Буква
у виразі, замість якої підставляються
числа, називається змінною. Змінну можна
позначити будь-якою буквою латинського
алфавіту. Записи
є виразами зі змінними. Якщо замість
букви (змінної) підставляти числа, то
будуть отримуватись різні числові
вирази. Наприклад, розглянемо вираз зі
змінною:
Якщо
,
то маємо числовий вираз
якщо
,
то числовий вираз буде
Отже,
змінна
– це знак (символ), який можна заміняти
числами. Числа, які можна підставляти
замість змінної, називаються значеннями
змінної, а множина таких чисел називається
областю визначення даного виразу. Можна
підставляти замість змінної тільки
такі її значення, при яких отримується
числовий вираз, який має смисл. Так у
вираз
не можна підставити замість х
число 3, бо числовий
вираз не буде мати смислу. Тобто областю
визначення даного виразу є множина
.
В
математиці розглядають вирази, які
містять одну, дві, три і т.д. змінні.
Наприклад:
тощо.
Отже, числові вирази утворюються з чисел, знаків дій та дужок, а у виразах зі змінними є ще і букви. Числові вирази, вирази зі змінною – це математичні слова, з яких утворюються математичні речення.
Питання для узагальнення
Який вираз називається виразом зі змінною?
Що називається областю визначення виразу зі змінною?
3. Тотожні перетворення виразу. Поняття тотожності
Означення. Два вирази називаються тотожно рівними, якщо при будь-яких значеннях змінної з області визначення виразів їх відповідні значення рівні.
Н.:
і
–
тотожно рівні вирази.
Означення. Тотожність – це рівність, що містить у собі невідоме, позначене буквою і справедливе при будь-якому значенні цієї букви.
Н.: a + b = b + a – тотожність.
Рівність, яка правильна при будь-яких значеннях змінної, називається тотожністю.
Тотожностями
є всі правильні числові рівності.
Прикладами тотожностей є закони
додавання, множення, правила віднімання,
ділення:
тощо. Тотожностями є правила дій з нулем
і одиницею:
тощо. Прикладами тотожностей є відомі
формули скороченого множення:
тощо.
Тотожні перетворення виразів – це заміна виразу тотожно рівним йому виразом.
Прикладами тотожних перетворень є:
а) розклад многочлена на множники різними способами – це винесення за дужки спільного множника, яке здійснюється на основі розподільного закону множення відносно додавання; групування, яке здійснюється на основі переставного і сполучного законів додавання; застосування формул скороченого множення тощо;
б) зведення подібних;
в) виконання дій з дробами; скорочення дробів або зведення дробів до спільного знаменника тощо.
В початковій школі виконують тотожні перетворення тільки числових виразів. Їх теоретичною основою є застосування законів множення, додавання, різних правил: додавання суми до числа чи числа до суми; віднімання суми від числа чи числа від суми та інших.
Наприклад.
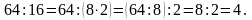
Отже, тотожностями є всі правильні числові рівності.
Питання для узагальнення
Які вирази називаються тотожно рівними?
Що називається тотожними перетвореннями виразів?