3. Подільність суми, різниці, добутку цілих невід’ємних чисел

Теорема про подільність суми на число. Якщо кожний доданок ділиться на натуральне число , то і їх сума ділиться на це число.

Дано:

Довести:

Доведення: так як ,

так як ,

,

.

Наприклад. 1) Якщо 45 9 і 18 9 то (45+18) 9, справді 15 + 18 = 63, 63 9.

2) 204 17, так як 204 = 170 + 34, то 170 17 34 17.

Теорема про неподільність суми на число. Якщо в сумі один з доданків не ділиться на число , а всі останні доданки діляться на число , то вся сума на число не ділиться.

Дано: (1)

,

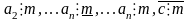
Довести: s

Доведення: (від супротивного). Припустимо що , тоді з рівності (1)

Так як і за теоремою про подільність суми , то за теоремою про подільність різниці , а це суперечить умові. Оже .

Наприклад, (190+13) не 19, так як 190 19 13 19.

Теорема про подільність різниці на число. Якщо числа а і b діляться на n і а ≥ b, то а – b теж ділиться на n.

Доведення аналогічне до теореми подільності суми.

Теорема про подільність добутку на число. Якщо один із співмножників добутку ділиться на натуральне число n, то і весь добуток ділиться на n.

Доведення. нехай а n, то а = n · q (·b)

a · b = (n · q) · b, звідси a · b = n · (q · b), але q · b – ціле невід’ємне число k, тоді a · b = n · k a · b n.

Наслідок: Якщо в добутку аb множник а ділиться на m, а множник b ділиться на n, то добуток аb ділиться на mn. Наприклад, 24∙36 ділиться на 108, бо 108 = 12∙9.

Отже, існують теореми подільності: про подільність суми на число, про подільність різниці на число і про подільність добутку на число.

Питання для узагальнення

• Які існують теореми подільності?

• Сформулюйте теорему подільності суми на число (різниці на число, добутку на число).

4. Ознаки подільності на 2 і 5, 4 і 25, 3 і 9 в десятковій системі числення

Ознака подільності на 2

Для того щоб число х ділилося на 5, необхідно і достатньо, щоб його десятковий запис закінчувався однією з цифр 0, 2, 4, 6, 8.

Ознака подільності на 5

Для того щоб число х ділилося на 5, необхідно і достатньо, щоб його десятковий запис закінчувався однією з цифр 0 або 5.

Доведення: Запишемо число а = а_na_n-1…a₀ у вигляді суми розрядних одиниць, яку розіб’ємо на два доданки: а = (а_n10ⁿ + … + a₁10) + a_0. Як бачимо, перший доданок ділиться і на 2, і на 5. Отже, щоб сума ділилась на 2 або на 5, необхідно і достатньо, щоб і другий доданок а₀ ділився відповідно на 2 або на 5. Теорему доведено.

Ознака подільності на 4 (25)

Для того щоб число х ділилося на 4, необхідно і достатньо, щоб на 4 ділилося двохзначне число, утворене двома останніми числами десяткового запису числа х.

Доведення: Число а = а_na_n-1…a₀ запишемо у вигляді суми двох доданків: а = (a_n10ⁿ + … +a₂10²) + (a₁10 + a₀). Перший доданок ділиться як на 4, так і на 25. Отже, число а як сума двох доданків ділиться на 4 (на 25) тоді і тільки тоді, коли на 4 (на 25) ділиться число а₁а₀ = а₁10 + а₀, утворене двома останніми цифрами числа а. Теорему доведено.

Ознака подільності на 3

Для того щоб число х ділилося на 3, необхідно і достатньо, щоб сума цифр його десяткового запису ділилася на 3.

Ознака подільності на 9

Для того щоб число х ділилося на 9, необхідно і достатньо, щоб сума цифр його десяткового запису ділилася на 9.

Доведення: Запишемо число а у вигляді: а = a_n10ⁿ + … + a₁10 + a₀.

Оскільки 10 = 9 + 1, 10² = 99 + 1, ... , 10ⁿ = +1,

то a_n ( 99..9 + 1) + … +a₁ (9 + 1) + a₀ = (a_n99..9 + … + a₁9) + (a_n + … + a₁ + a₀).

Перші доданки суми діляться як на 3, так і на 9.

Отже, для того щоб число а ділилось на 3 або на 9, необхідно і достатньо, щоб сума одноцифрових чисел, виражених його цифрами (сума цифр) a_n+ … + a₁ + a_0, ділилась на 3 або на 9. Теорему доведено.

Отже, доведені вище ознаки подільності дають змогу визначити подільність чисел на 2, 3, 4, 5, 9 і 25.

Питання для узагальнення

• Яка ознака подільності на 2 (5)?

• Яка ознака подільності на 4 (25)?

• Яка ознака подільності на 3 (9)?