Міністерство освіти і науки України

Комунальний вищий навчальний заклад

«Бериславський педагогічний коледж імені В. Ф. Беньковського»

Херсонської обласної ради

Предмет: Основи початкового курсу математики Модуль № 1 Семестр: V Кількість годин: 2

Лекція № 5 (31-32)

Тема: Теоретико-множинний зміст суми двох цілих невід’ємних чисел

Розглянуто і затверджено на засіданні предметної (циклової) комісії викладачів фізико-математичних дисциплін та нових інформаційних технологій Протокол № ___ від _________ 2013р. Голова предметної (циклової) комісії: _________________ Г. Ю. Шкворченко

м. Берислав

Тема лекції: Теоретико-множинний зміст суми двох цілих невід’ємних чисел

Студенти повинні знати:

• означення суми цілих невід’ємних чисел;

• закони додавання;

• означення відношення «менше» через додавання;

• умови існування і єдиності суми цілих невід’ємних чисел.

Студенти повинні вміти:

• знаходити суму цілих невід’ємних чисел;

• застосовувати закони додавання для виконання обчислень раціональними способами;

• використовувати теоретико-множинне поняття дії додавання.

Тип лекції: тематична

Ключові поняття: доданок, сума, переставний закон, сполучний закон додавання.

План

1. Теоретико-множинний зміст суми цілих невід’ємних чисел.

2. Існування суми, її єдність.

3. Закони додавання:

   1. Переставний закон додавання.

   2. Сполучний закон додавання.

4. Визначення відношення «менше» через додавання.

Основна література

1. Кухар, В. М. Теоретичні основи початкового курсу математики [Текст] : навч. посібник для педучилищ / В. М. Кухар, Б. Л. Білий. – К. : Вища школа, 1987. – С. 169-174.

2. Основи початкового курсу математики [Текст] : навчально-методичний посібник / укл. Л. М. Голець, О. О. Кислякова, І. А. Ляшенко, О. Г. Онуфрієнко. – Запоріжжя, 2010. –

С. 33-35.

3. Стойлова, Л. П. Основы начального курса математики [Текст] : учеб. пособие для учащихся педучилищ / Л. П. Стойлова, А. М. Пишкало. – М. : Просвещение, 1988. – С. 128-135.

Інтернет-ресурси

1. Законы сложения [Электронный ресурс] : теоретические материалы / сайт shkolo.ru. // Режим доступу: http://shkolo.ru/zakonyi-slozheniya. – Название с экрана.

2. Сложение натуральных чисел [Электронный ресурс] : теоретические материалы // сайт shkolo.ru. – Режим доступу: http://shkolo.ru/slozhenie-naturalnyih-chisel. – Название с экрана.

Структура лекції

І. Вступна частина:

1. Оголошення теми, мети і завдань лекції.

2. Ознайомлення з планом лекції, основною та додатковою літературою.

ІІ. Виклад лекційного матеріалу (згідно плану та вимог до лекції)

1. Теоретико-множинний зміст суми цілих невід’ємних чисел

1. Підготовча робота

• Що називається об’єднанням двох множин і ?

• Знайдіть , якщо

1) , ;

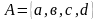2) , .

• Якими законами володіє операція об’єднання множин?

• Сформулюйте переставний закон об’єднання, сполучний закон об’єднання множин.

Задача 1. Ірина знайшла 3 гриба, а Ніна 4 гриба. Скільки всього грибів знайшли дівчата?

Розв’язання.

4+3=7 (гр.)

Відповідь: 7 грибів.

• Чому ця задача розв’язується дією додавання?

Зобразимо кожен гриб, який знайшла Ірина кружечком, а гриби, які знайшла Ніна трикутником.

○ ○ ○ ○

∆ ∆ ∆

Щоб відповісти на запитання задачі треба до грибів Ірини приєднати гриби Ніни, тобто треба об’єднати дві множини грибів і підрахувати, скільки елементів в об’єднанні цих множин.

Отже ми бачимо, що додавання цілих невід’ємних чисел тісно пов’язане з операцією об’єднання множин.

Задача 2. Дано дві множини: , 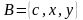, , 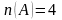. Знайдемо

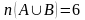
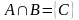Ми бачимо, що . Чому? В цій задачі , тому

Отже, сума цілих невід’ємних чисел визначається через об’єднання неперетинаючихся множин.

Означення. Сумою двох цілих невід’ємних чисел а і b називається число елементів в об’єднанні множин А і В, які не перетинаються і таких, що n (А) = а, п (В) = b, тобто а + b = п (А В), де а = п (А), b = п (В), А В = .

Символічно це означення можна записати так:

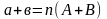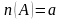, де , , А В =

Наприклад, поясніть, користуючись даним означенням, чому 3+5=8.

3 – це число елементів деякої множини А, 5 – це число елементів деякої множини В, причому А В = . Наприклад, 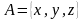, 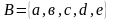. . Шляхом перелічування знайдемо, що . Отже 3 + 5 = 8.

Множини А і В можна брати довільні, так як сума не залежить від вибору неперетинаючихся множин.

Отже, сума цілих невід’ємних чисел визначається через об’єднання неперетинаючихся множин.

Питання для узагальнення

• Що називається сумою двох цілих невід’ємних чисел?