4. Зображення множин і зв’язків між ними за допомогою кругів Ейлера

З геометричної точки зору множини зображуються на площині кругами Ейлера. В середині круга містяться елементи множини.

Наочне зображення множин

А={а, в, с}

А

1. Нехай маємо множини:

А={а, в, с}

В={1, 2, 3}

Очевидно, що множина А і В не містять спільних елементів, тобто вони не перетинаються.

А В

А В – різні

2. Розглянемо множини:

А={m, n, k, f}

В={f, k, a, c}

Множини А і В мають спільні елементи f та k.

А В

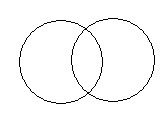
3. Множини А={а, в, с}

В={а, в, с}

А = В – множини рівні

4. А={а, в, с, d}

В={а, в}

Кожен елемент множини В, є елементом множини А. В такому випадку говорять, що множина В є підмножиною множини А.

А

В А

Отже, множини і операції над ними зручно ілюструвати наочно за допомогою кругів Ейлера (або діаграм Ейлера – Венна).

5. Операції над множинами. Закони операцій

1. Перетин (переріз) множин і його закони

Нехай дані дві множини:

А={2, 4, 6, 8} та В={5, 6, 7, 8, 9}.

Утворимо множину С, в яку включимо спільні елементи множин А та В: С = {6, 8}. Так, отриману множину С називають перерізом множин А та В.

Означення. Перерізом множин А і В називається множина, яка містить тільки такі елементи, які належать множині А та множині В.

Переріз множин А і В позначають АВ. Отже, якщо а є А∩В, то а є А і а є В; тобто А∩В = {x | x є A і х є В}.

Якщо зобразити множину А і В за допомогою кругів Ейлера, то переріз даних множин зобразиться заштрихованою областю.

У випадку, коли множини А і В не мають спільних елементів, говорять, що їх перетин пустий (не перетинаються): АВ=

Визначення перерізу множин:

хАВхА та хВ

Якщо елементи множин А і В перелічені, то щоб знайти АВ, достатньо перерахувати елементи, які належать А і В, тобто їх спільні елементи.

А як бути, якщо множини задані за допомогою характеристичних властивостей перерізаних за допомогою сполучника «і».

Найдемо, наприклад, переріз множини А – парних натуральних чисел та множини В – двозначних натуральних чисел. Характеристична властивість елементів множини А – «бути парним натуральним числом», характеристична властивість елементів множини В – «бути двозначним натуральним числом». Тоді, згідно визначенню, елементи перерізу даних множин повинні мати властивість «бути парним та двозначним натуральним числом». Таким чином, множина АВ складається з парних двозначних чисел. Отримана множина не пуста, так як, наприклад, 24АВ, оскільки число 24 парне та двохзначне.

Вияснимо тепер, що представляє собою переріз множини А – парних натуральних чисел та множина В – натуральних чисел, кратних 4. Дані множини безкінечні, та множина В – підмножина множини А. Тому, елементами, які належать множині А та множині В, будуть елементи множини В. Тобто, АВ=В