Тема 2: Построение схем и исследование двухпозиционной системы автоматического регулирования (сар).

Цель работы: Построить дискретную динамическую модель (ДДМ) процесса, происходящего при изменении уровня жидкости в сосуде. На основании полученной ДДМ и задачи поддержания уровня в заданных, пределах получить логическое выражение, описывающее работу двухпозиционного регулятора. По полученному логическому выражению собрать схему двухпозиционного регулирования. Ознакомится с принципом действия и методами расчета параметров переходных процессов в двухпозиционной САР.

К

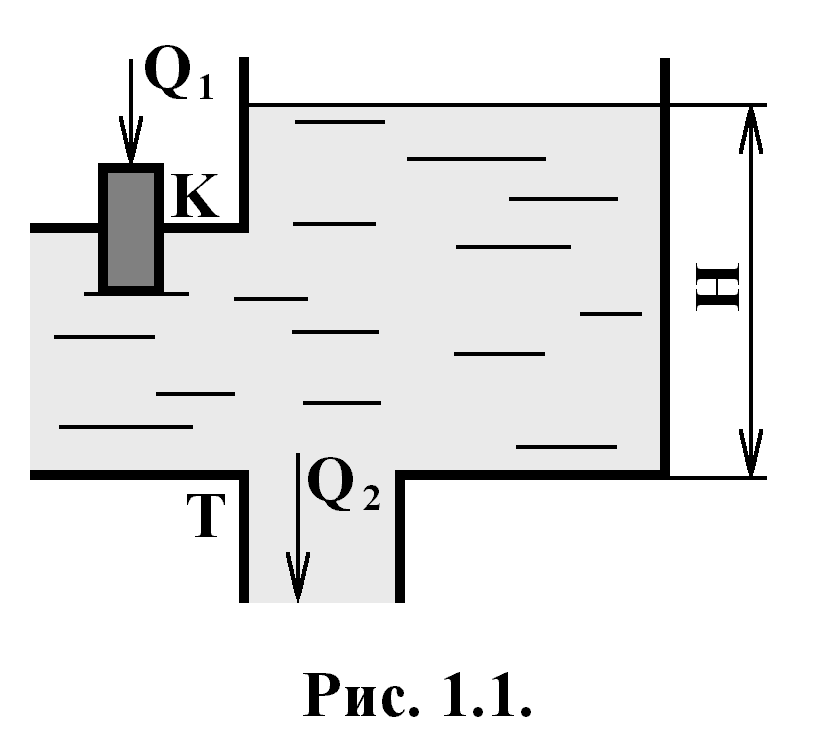
Рисунок 2.1

раткие теоретические пояснения: При математическом моделировании объект управления рассматривается как преобразователь входных сигналов в выходные. В объекте управления (ОУ) можно выделить две входные величины: возмущающее воздействие, которое стремится изменить расход энергии (вещества), и регулирующее воздействие, которое влияет на изменение притока энергии (вещества). Если входные величины равны между собой, то значение регулируемого параметра становится постоянным, и такой режим работы объекта называется статическим режимом. Неравенство между потоком и расходом энергии (вещества) в объекте приводит к изменению регулируемого параметра, при этом скорость изменения пропорциональна разности между двумя входными величинами. Такой режим работы ОУ называется динамическим режимом. Динамический режим является наиболее характерным для ОУ. Математической моделью ОУ являются уравнения материального и энергетического баланса, которые для статического режима работы являются линейными, а для динамического – дифференциальными.

П

Рисунок 2.1

римером одного из ОУ может служить бак (рисунок 2.1.), жидкость в который поступает через клапан К и вытекает по трубе Т. Изменение притока жидкости для данного ОУ является входным возмущающим воздействием, а изменение уровня Н – выходным параметром. В установившемся режиме приток жидкости в бак равен её расходу, и уровень Н остаётся постоянным.

Уравнения материального баланса ОУ, в котором каждому значению возмущающего параметра в установившемся режиме соответствует определённое значение регулируемого параметра, называется статическим ОУ. Статический режим описывается выражением (2.1):

Q₁ - Q₂ = 0; (2.1)

Для статических ОУ характерно самовыравнивание.

Самовыравнивание – свойство ОУ приходить в новое состояние равновесия после возмущения без вмешательства регулятора.

Динамику изменения уровня жидкости в баке можно описать дифференциальным уравнением первого порядка:

(2.2)

где T_a – время разгона объекта, в течении которого выходная величина достигает 99% значения, соответствующего новому значению равновесия;

Н – регулируемый параметр, уровень жидкости в баке;

ρ – коэффициент самовыравнивания, характеризует влияние на небаланс степени отклонения регулируемого параметра;

Q₁ – приток жидкости в бак;

Q₂ – расход жидкости из бака;

Разделив уравнение (2.2) на ρ получим:

(2.3)

г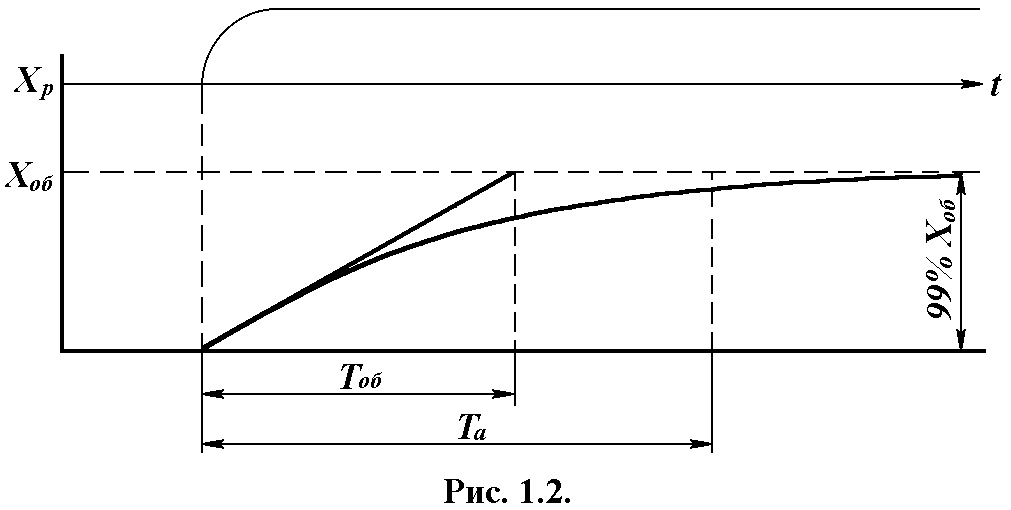 де Т_об = T_a / ρ – постоянная времени объекта, характеризует время достижения нового установившегося значения регулируемого параметра, при условии изменения регулируемого параметра с постоянной скоростью;

К_об = 1 / ρ – коэффициент усиления или передачи объекта.

Ч

Рисунок 2.2

ем больше Т_об, тем более инерционным является ОУ и тем труднее его регулировать. Уравнение, описывающее изменение регулируемого параметра во время переходного процесса, при скачкообразном возмущении называется – уравнением кривой разгона объекта, а кривая изменения регулируемого параметра во время переходного процесса – кривой разгона объекта (рисунок 2.2).

Выходной сигнал X_об ОУ при скачкообразном возмущении X_Р изменяется по экспоненте и стремится к новому установившемуся значению. Чем больше Т_об, тем больше длительность переходного процесса. Постоянная времени Т_об определяется, как отрезок на линии установившегося значения X_об, отсекаемый перпендикуляром, проведённым из точки, через которую проводится касательная и точкой пересечения касательной с линией установившегося значения.

Е

Рисунок 2.3 Рисунок 2.4

сли постоянная времени объекта равна нулю (Т_об = 0), то объект называется безинерционным. В объектах, у которых постоянная времени объекта стремится к бесконечности (Т_об → ∞) процесс регулировать нельзя.

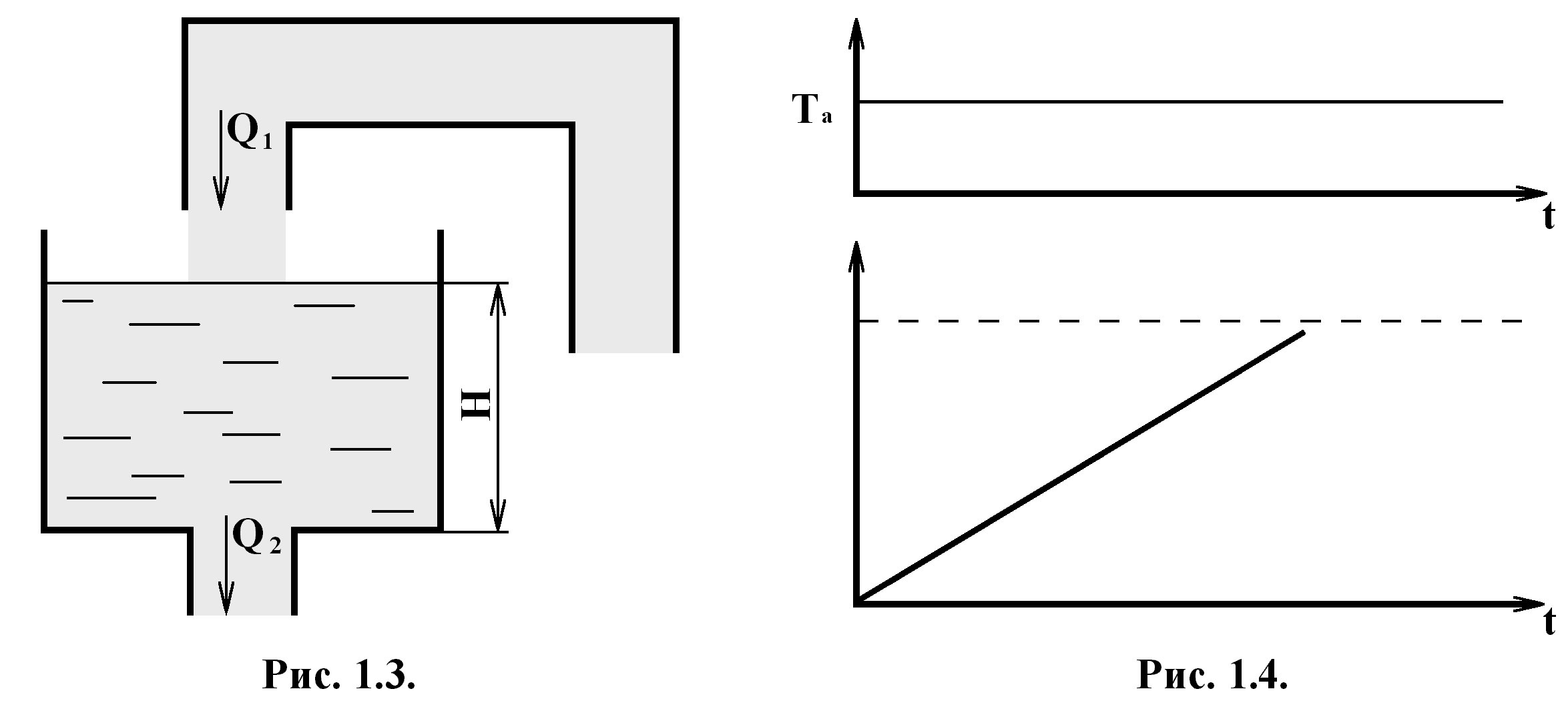В объекте, приведённом на рисунке 2.3 жидкость в бак подаётся сверху, а выход жидкости происходит самотёком. В этом объекте установившийся режим возможен только при равенстве производительности насоса и расхода жидкости вытекающей из бака. Причём величина уровня жидкости не влияет ни на приток, ни на расход жидкости. При изменении Q₁ или Q₂ происходит изменение уровня жидкости с постоянной скоростью. Этот ОУ не обладает самовыравниванием. Уравнение динамики этого ОУ будет:

(2.4)

Откуда: (2.5)

Так как выходной сигнал объекта пропорционален интегралу от значений входных сигналов, то такой объект называют интегрирующим или астатическими объектом. Время разгона объекта (Т_а) определяет время, в течении которого ёмкость объекта заполняется или опорожняется при максимальной разности между притоком и расходом. Переходная характеристика такого объекта имеет вид, показанный на рисунке 2.4. Из этого графика следует, что при подаче на вход астатического объекта скачкообразного возмущения выходной сигнал изменяется с постоянной скоростью и не стремится к какому-либо установившемуся значению, и такие объекты называют нейтральными.

Для регулирования какого-либо параметра в ОУ применяются автоматические регуляторы. По виду регулирующего воздействия они подразделяются на: регуляторы непрерывного действия и регуляторы дискретного действия. В регуляторах непрерывного действия перемещение регулирующего органа происходит непрерывно при изменении регулируемого параметра, а в регуляторах дискретного действия перемещение регулирующего органа происходит скачком при достижении регулируемым параметром заданного предельного значения. Регуляторы дискретного действия являются позиционными регуляторами. Регулирующее воздействие у позиционных регуляторов может принимать два или три фиксированных значения (позиции), при определённых значениях регулируемого параметра. 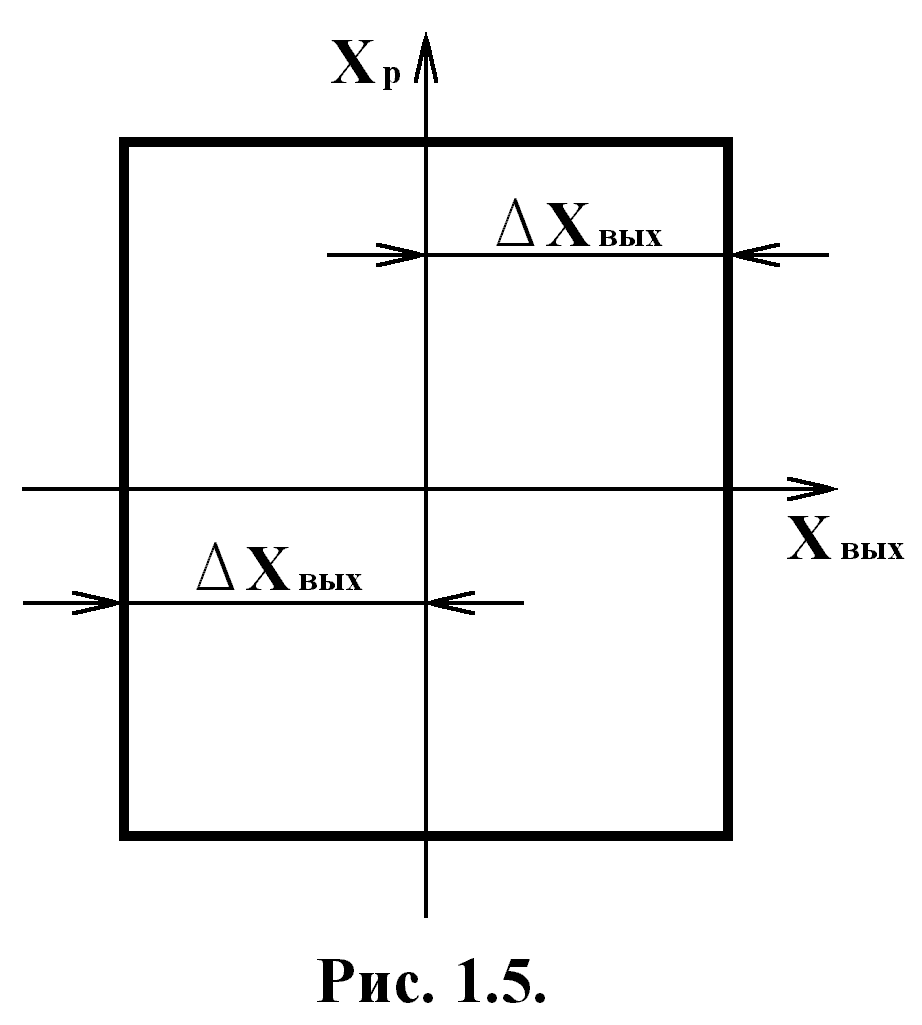В зависимости от числа позиц ий, регуляторы могут быть: двухпозиционными и трёхпозиционными. У двухпозиционных регуляторов регулирующий орган может иметь только два положения – открытое (включённое) или закрытое (отключённое). Статическая характеристика реального двухпозиционного регулятора приведена на рисунке 2.5. При возрастании во времени отклонений регулируемого параметра регулирующий орган срабатывает скачком при Х_вых= +Δ Х_вых, а при обратном х

Рисунок 2.5

оде Х_вых регулятор срабатывает при Х_вых=-Δ Х_вых; где Х_вых – нечувствительность регулятора.

Рассмотрим работу двухпозиционного регулятора более подробно.

Если регулирующий орган занимает положение Х_{p min}, соответствующее минимальному регулирующему воздействию на объект, то регулируемый параметр Х увеличивается до значения Х_{вых max}. При достижении параметром этого значения, регулирующий орган переключается в положение Х_{р max}. В положении Х_{р max} регулирующее воздействие превышает действие всех возмущений, вызывающих отклонение регулируемого параметра. Регулируемый параметр Х начинает уменьшатся до Х_{вых min}. При Х_{вых min} регулирующий орган переключается в положение Х_{p min} и регулирующее воздействие на ОУ становится минимальным, а регулируемый параметр Х начинает опять увеличиваться. Таким образом регулируемый параметр Х совершает незатухающие колебания, которые называются автоколебаниями. Амплитуда и частота автоколебаний зависит от диапазона настройки регулятора: Х_{вых max} и Х_{вых min}, а также от инерционности объекта. Позиционные регуляторы применяются на объектах с большой ёмкостью и малым запаздыванием.

Поставим в соответствие единичному значению логической переменной Х превышение выходной величины объекта Х_{вых min}, а нулевому значению этой переменной – непревышение Х_{вых min}. Аналогично, примем Х₂= 1, если имеет место превышение Х_{вых max} и Х₂= 0, если нет превышения Х_{вых max}. Состояние объекта, когда Х_вых < Х_{вых min}, можно охарактеризовать логическим произведением . Если же Х_вых < Х_{вых max} или Х_вых > Х_{вых min}, то такому состоянию объекта можно поставить в соответствие логическое произведение . Состояние объекта, когда Х_вых > Х_{вых max} можно охарактеризовать логическим произведением Х₁ Х₂. Состояние объекта, когда Х_вых < Х_{вых max} и Х_{вых min} > Х_{вых max}, физически неосуществимо, поэтому соответствующее этому состоянию произведение логических переменных Х₁ Х₂ равно нулю, те Х₁ Х₂= 0. Поэтому реально осуществимые состояния объекта можно представить следующим образом:

(2.6)

(2.7)

(2.8)

Обозначим символом → переход из одного состояния в другое. Тогда процесс перехода объекта между этими состояниями можно отобразить следующим образом:

⇄ ⇄ (2.9)

Выражение (2.9) представляет собой описание дискретной динамической модели (ДДМ) процесса, происходящего в объекте. Из (2.9) видно, какие состояния объектов реально могут существовать, и как осуществляется переход между этими состояниями. Имея ДДМ процесса и задачу, поставленную перед позиционным регулятором можно получить логическое выражение, описывающее работу двухпозиционного регулятора.

Пусть например, требуется получить формулу работы двухпозиционного регулятора, который включает регулирующий орган (у = 1) тогда, когда выходной параметр превышает Х_{вых min} (Х₂= 1) и оставляет его включённым до тех пор пока Х_{вых min} < Х_вых < Х_{вых max}. Участок процесса, отображаемого выражением (2.9), на котором происходит включение регулирующего органа, можно представить:

(2.10)

Где символом обозначено условие включения регулирующего органа, в каком-либо состоянии объекта. Следовательно, регулирующий орган должен включатся тогда, когда объект находится в состоянии соответствующем Х₂ или, когда осуществлён переход из Х₂ в и далее в .

Логическое выражение, описывающее работу регулятора, как следует из (2.10), записывается следующим образом:

(2.11)

Имея выражение (2.11), можно построить схему автоматического двухпозиционного регулятора.

Допустим, что требуется реализовать выражение (2.11) на логических элементах И-НЕ. Выражение (2.11) можно представить следующим образом:

(2.12)

где .

Откуда следует, что y = z и, следовательно, .

Преобразуем полученное выражение:

. (2.14)

Из (2.10) следует, что двухпозиционный регулятор должен содержать: датчики регулируемого параметра (Х₁ и Х₂) и 3 логических элемента И-НЕ.

Описание лабораторной установки:

Лабораторная установка (рисунок 2.6) включает в себя насос и два бака. Бак 1 связан нагнетающим трубопроводом (резиновым шлангом) насоса, а бак 2 с всасывающим трубопроводом. Вода из бака 1 сливается в бак 2. В баке 1 установлен поплавковый датчик уровня, связанный с контактной схемой автоматического регулятора, включение которого в работу осуществляется при положении “контактная” переключателя режимов (ПР). кроме того в баке 1 установлены датчики верхнего и нижнего уровней, связанные с бесконтактной схемой автоматического регулятора, которая включается в работу при положении “бесконтактная” переключателя режимов (ПР).

Б

Рисунок 2.6

есконтактная схема автоматического регулятора собирается студентами. Для этого на стенде установлены три логических элемента “ИЛИ-НЕ”, два зажима “верхний контакт” и “нижний контакт” связанные соответственно с датчиками верхнего и нижнего уровней, зажим “электродвигатель”, связанный с электродвигателем насоса. Напряжение на стенд подаётся автоматическим выключателем (АВ) и контактором УЗОШ.

Рисунок 2.6

П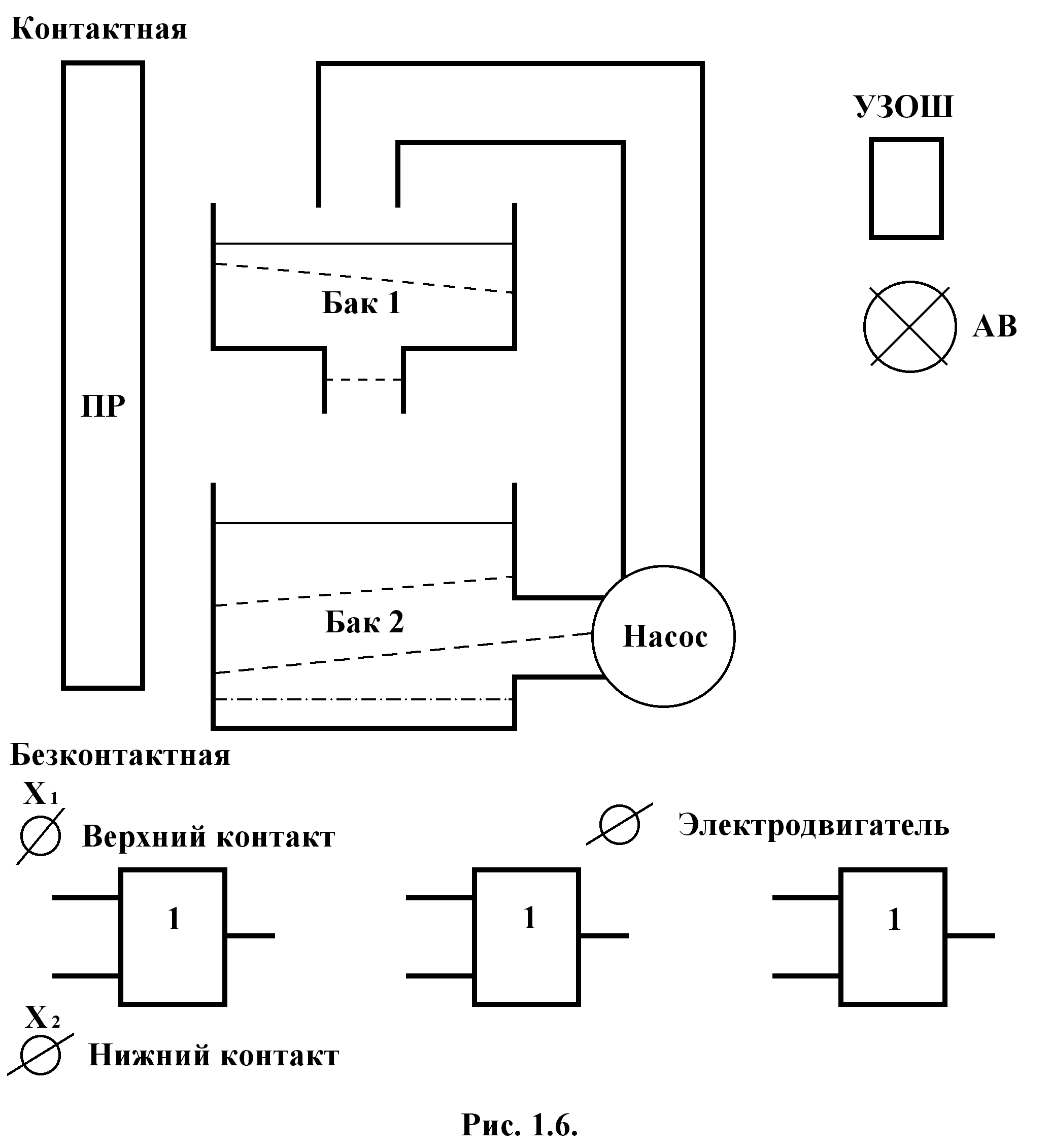 орядок выполнения работы:

1. Заполнить бак 2 водой;

2. Переключатель режимов ПР поставить в положение “контактная”;

3. Подать напряжение на схему, включив выключатель АВ и контактор УЗОШ.

4. Снять кривую разгона объекта и определить параметры Т_об, Х_об, Т_а, показанные на рисунке 2.2;

3. Зафиксировать установившийся процесс в системе автоматического регулирования;

4. Отключить выключатель АВ;

5. Дать описание дискретной динамической модели процесса, измерения уровня воды в баке 1;

6. По модели процесса и задаче поддержания уровня в баке 1 между верхним и нижним контактами получить логическое выражение, описывающее работу регулятора;

7. Привести реализацию полученного выражения на логических элементах “ИЛИ-НЕ” и показать преподавателю;

8. Собрать синтезированную студентом схему бесконтактного автоматического регулятора;

9. После проверки схемы преподавателем, поставить переключатель ПР в положение “бесконтактное” и включить выключатель АВ и контактор УЗОШ;

10. Повторить операции по пункту 5;

11. Отключить выключатель АВ;

12.Оформить отчёт и проверить свои знания по контрольным вопросам.