Тема 7. Определение областей устойчивости (метод d-разбиения)

Цель практического занятия: Научиться строить кривую D-разбиения, наносить на нее штриховку определять область устойчивости одного регулируемого параметра .

Теоретические сведения: лекция 7, 8.

План практического занятия:

1. Составить уравнение регулируемого параметра .

2. Выделение вещественной и мнимой составляющих уравнения регулируемого параметра .

3. Вычисление вещественной и мнимой составляющих уравнения регулируемого параметра  для значений частоты  от минус бесконечности до плюс бесконечности (-    ) и сведение результатов в таблицу.

4. Построение кривой D-разбиения на плоскости регулируемого параметра  и нанесение штриховки.

5. Определение области устойчивости регулируемого параметра .

6. Проверка результатов вычисления с помощью любого из критериев устойчивости.

Пример решения задачи:

Условие: Для системы автоматического управления с характеристическим уравнением: , где Т₁ = 0,5 с; Т₂ = 0,1 с; Т₃ = 1, с выделить область устойчивости по коэффициенту  и определить значение коэффициента , соответствующее границе устойчивости.

Решение:

1. Подставляем в характеристическое уравнение значения постоянных времени и получаем характеристическое уравнение вида:

.

Решаем полученное уравнение относительно коэффициента  и получаем следующее выражение:

.

2. Подставляем в полученное выражение чисто мнимое значение комплексного переменного: ѕ = jω и получаем коэффициент передачи  в виде комплексного числа:

.

Выделяем вещественную (Re (ω)) и мнимую составляющие (Jm (ω)):

Re (ω) = _; Jm (ω) = _.

_{3. Для построения области устойчивости необходимо построить кривую D-разбиения, которая должна охватывать диапазон частот от -∞ до +∞. Для облегчения построения искомой кривой построим сначала часть кривой D-разбиения, охватывающую диапазон частот от 0 до + ∞, а затем построим часть кривой D-разбиения, охватывающую диапазон частот от - ∞ до 0, зеркально отобразив построенную часть кривой для диапазона частот от 0 до + ∞ относительно вещественной оси. Для построения части кривой D-разбиения для диапазона частот от 0 до + ∞ заполняем таблицу, определив предварительно точки пересечения части кривой с осями координат.}

_{Чтобы определить частоты и координаты точек пересечения части кривой с вещественной осью приравниваем к нулю мнимую составляющую: .}

_{Решая полученное уравнение, определяем, что часть кривой пересекает вещественную ось при частотах ω = 0 и ω = 5,66. Подставляем найденные значения частоты в вещественную составляющую и находим координаты точек пересечения части кривой с вещественной осью: т. А (-1; j0) и т. В (5,66; j0).}

_{Для определения частот и координат точек пересечения части кривой с мнимой осью поступим аналогичным образом, приравняв к нулю вещественную составляющую:} .

Получим, что часть кривой D-разбиения пересекает мнимую ось при частоте _{ω = 1,24, координаты точки пересечения С (0; -j1,89).}

Выбрав несколько промежуточных значений частоты, находящиеся между частотами пересечения с осями координат заполняем таблицу 6:

Таблица 6 – Данные для построения кривой Dбиения

ω	0	1	1,24	3	5	5,66	10	100	+∞
Re(ω)	-1	-0,35	0	4,85	15,25	19,82	64	6499	+∞
Jm(ω)	0	-1,55	-1,89	-3,45	-1,75	0	34	49840	+∞

4. По значениям таблицы строим часть кривой D-разбиения для диапазона частот от 0 до + ∞, и зеркально отобразив построенную часть кривой относительно вещественной оси для получения полной кривой D-разбиения для диапазона частот от - ∞ до + ∞. Нанесем штриховку слева от кривой D-разбиения при изменении частоты от - ∞ до + ∞. Полученная кривая приведена на рисунке.

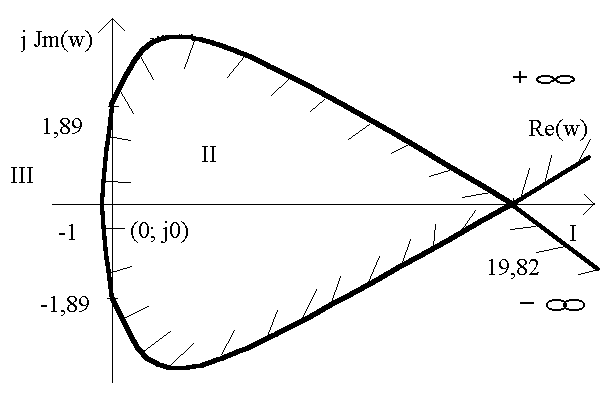
Рисунок 7 – Кривая D-разбиения.

5. Областью устойчивости является замкнутая область внутрь, которой направлена штриховка, а это II область для нашего случая.

6. Проверим правильность нахождения области устойчивости. Для этого выберем, какое либо значение коэффициента , принадлежащее найденной области устойчивости и находящееся на вещественной оси, например  = 10, и проверим систему на устойчивость по любому из критериев устойчивости. Воспользуемся критерием Гурвица. После подстановки в характеристическое уравнение, выбранное значение коэффициента передачи  получаем характеристическое уравнение вида:

.

Составляем главный определитель Гурвица и определители Гурвица более низкого порядка и вычисляем их значение:

	0,65	11	0
Δ3 =	0,05	1,6	0	= 5,39 > 0;
	0	0,65	11

Δ2 =	0,65	11	= 0,49 >0;
	0,05	1,6

Δ1 =

0,65

= 0,65 > 0.

Все определители Гурвица положительны, система устойчива.

Вывод: область устойчивости найдена, верно, значение коэффициента , соответствующее границе устойчивости  = 19,82.

Литература: 1, стр. 193-196; 2, стр. 188-190.