Тема 5. Определение устойчивости сау по частотному критерию Михайлова

Цель практического занятия: научиться строить годограф Михайлова и определять устойчивость САУ по критерию Михайлова.

Теоретические сведения: лекция 7.

План практического занятия:

1. Выделение вещественной и мнимой составляющих из характеристического полинома.

2. Вычисление вещественной и мнимой составляющих характеристического полинома при различных значениях частоты  от нуля до плюс (0    +) бесконечности и сведение результатов вычисления в таблицу.

3. Построение годографа Михайлова.

4. Определение устойчивости САУ по виду годографа Михайлова.

Пример решения задачи:

Условие: Характеристическое уравнение D(s) система имеет вид: . Определить устойчивость системы автоматического управления, ис­поль­зуя критерий устойчивости Михайлова.

Решение:

1. Из характеристического уравнения получаем характеристический полином в котором заменяем s на jω и выделяем вещественную и мнимую составляющую:

.

Выделяем вещественную и мнимую составляющую характеристического полинома:

; .

2. Для построения годографа Михайлова необходимо заполнить таблицу3, опре­делив вещественную и мнимую составляющую годографа при изменении частоты ω от 0 до +∞ (0 ≤ ω≤ + ∞ ).

Таблица 3 – Данные для построения годографа Михайлова

ω	0	2	5	10	50	∞
Re(ω)	15	75	3015	49515	31237515	∞
Jm(ω)	0	-50	-350	-1450	-37250	- ∞

3. По результатам вычислений строим годограф Михайлова.

Рисунок 4 - Годограф Михайлова

Годограф Михайлова начинается на вещественной полуоси, движется по часовой стрелке и располагается в одном квадранте, хотя степень характеристического уравнения n = 4, значит система неустойчива.

Вывод: САУ неустойчива.

Литература: 1, стр. 182-184; 2, стр. 185-188.

Тема 6. Определение устойчивости сау по частотному критерию Найквиста и по виду логарифмических частотных характеристик

Цель практического занятия: научиться определять устойчивость замкнутой САУ если известна передаточная функция разомкнутой САУ; научиться определять устойчивость САУ по виду ЛАЧХ и ЛФЧХ.

Теоретические сведения: лекции 3, 4, 7.

План практического занятия:

1. Определение устойчивости разомкнутой САУ по любому из критериев устойчивости.

2. Построение годографа Найквиста.

3. Определение устойчивости замкнутой САУ по виду годографа Найквиста.

4. Определение устойчивости замкнутой САУ по виду ЛАЧХ и ЛФЧХ.

Пример решения задачи:

Условие: Дана передаточная функция разомкнутой САУ , определить устойчивость замкнутой САУ созданной на базе этой разомкнутой САУ, проверить результат с помощью построения логарифмических частотных характеристик (ЛАЧХ и ЛФЧХ).

Решение:

1. Для определения устойчивости разомкнутой САУ воспользуемся правилом определения устойчивости по расположению корней характеристического уравнения, которое можно получить из характеристического полинома (характеристический полином находится в знаменателе передаточной функции). Характеристическое уравнение будет иметь вид:

,

отсюда найдем корни характеристического уравнения: s₁ = 0 и s₂ = - 5.

Разомкнутая система находится на апериодической границе устойчивости, т.к. один из корней равен нулю, а второй корень является «левым». Поэтому имеем дело с первым случаем определения устойчивости по критерию Найквиста.

2. Для построения годографа Найквиста необходимо из частотной передаточной функции выделить вещественную и мнимую составляющую и, принимая значения частоты  от 0 до +, заполнить таблицу 4, как было рассмотрено в практическом занятии 1.

Частотная передаточная функция:

,

отсюда:

; .

Таблица 4 – Данные для построения годографа Найквиста

ω	0	1	5	10	50	100	500	+ ∞
Re(ω)	-20	-19,23	-100	-4	-0,198	-0,049	-0,0019910-3	0
Jm(ω)	- ∞	-9,6	-10	-2	-0,0198	-2,49´10-3	-1,99´10-5	0

По результатам вычислений строим годограф Найквиста.

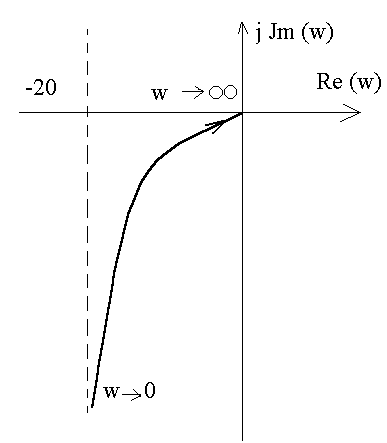
Рисунок 5 – Годограф Найквиста

3. Замкнутая САУ устойчива, т.к. годограф Найквиста не охватывает точку с координатами (-1 ; j0).

4. Данная передаточная функция соответствует интегрирующему звену с замедлением. ЛАЧХ такого звена может быть найдена по формуле (4.63):

, однако ее можно построить проще. ЛАЧХ интегрирующего звена с замедлением представляет собой ломаную линию, состоящую из двух отрезков: первый отрезок имеет наклон –20 дБ/дек и проходит через точку (4.46): , при частоте излома (4.21): , она ломается еще на – 20 дБ/дек и имеет наклон – 40 дБ/дек. ЛФЧХ будем строить, зная, что (4.62): , задаваясь такими же значениями частоты, как и при построении годографа Найквиста. Результаты вычислений сведем в таблицу 5:

Таблица 5 – Данные для построения ЛАЧХ и ЛФЧХ

ω	0	1	5	10	50	100	500	+ ∞
Тω	0	0,2	1	2	10	20	100	+ ∞
φ(ω), град	-90	-101,3	-135	-153,4	-174,2	-177,1	-179,4	-180

Строим ЛАЧХ и ЛФЧХ.

Р

исунок 6 – ЛАЧХ и ЛФЧХ

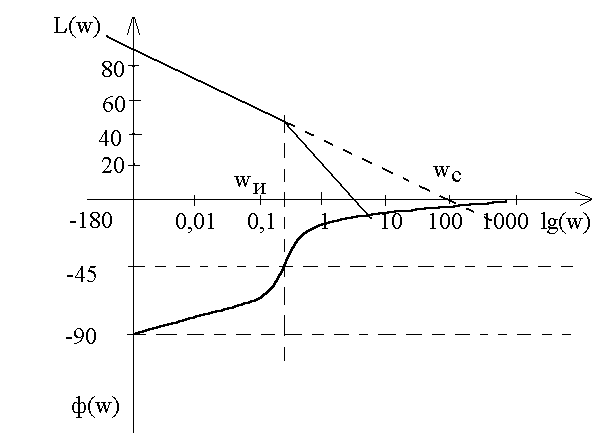
Система устойчива, т.к. частота, при которой ЛАЧХ пересекает ось частот меньше, частоты при которой ЛФЧХ достигает фазы –π ( -180º ).

Вывод: Замкнутая САУ устойчива.

Литература: 1, стр. 184-190; 2, стр. 190-194.