Тема 2. Моделирование де­терминированных информаци­онных процессов

В данной теме рассматриваются основные технологии работы с базовыми математическими технологиями преобразования логической, числовой информации. Вводится основные понятия множества, высказывания. Рассматриваются основные системы счисления и операции в них.

2.1. Понятие множества

Основное и самое существенное в понятии множества – это акт объединения различных объектов в одно целое.

Основатель теории множеств немецкий математик и философ Георг Кантор писал: «Под многообразием или множеством я понимаю вообще всякое многое, которое можно мыслить как единое, т.е. всякую совокупность определенных элементов, которая может быть связана в одно целое с помощью некоторого закона». Перефразируя Кантора можно сказать, что множество — любая совокупность определенных и различимых между собой объектов, рассматриваемых как единое целое. Природа таких объектов может быть совершенно любой.

Существенными в понятии множества являются следующие признаки:

1. Объекты, входящие во множество, определенные. Это означает, что для каждого объекта можно однозначно сказать, принадлежит ли он данному множеству или нет.

2. Объекты, входящие во множество, различимы между собой. Следовательно, во множестве не может быть двух или более одинаковых объектов.

3. Все объекты, входящие во множество, мыслятся как единое целое. Этим подчеркивается, что все объекты рассматриваются в совокупности, а от свойств отдельных объектов абстрагируются.

Множества обычно обозначают прописными курсивными буквами латинского алфавита: A, B, C и т.д. Для наиболее важных числовых множеств приняты постоянные обозначения. Множество натуральных чисел стандартно обозначается буквой N, множество целых чисел – С, множество действительных чисел – буквой R.

Объекты, составляющие данное множество, называют его элементами и обозначают строчными курсивными буквами латинского алфавита: а, x, y. Для того, чтобы указать, что x – элемент множества А, записывают xÎ A (читается: «x принадлежит А»). Например, если А – множество дней недели, а x – понедельник, то xÎ A. Чтобы указать, что x не является элементом множества А, записывают xÏА («x не принадлежит А»). В нашем примере, если x – ноябрь, то xÏА.

Из канторовского понятия множества следует, что задать множество можно двумя способами. Первый способ – явный или перечислительный – состоит в простом перечислении всех элементов, в совокупности составляющих данное множество. Элементы множества заключаются в фигурные скобки { }, которые показывают, что элементы объединены в одно целое, в совокупность.. Если А – множество дней недели, то записывают А={понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, множество арифметических действий B задают так: B={сложение, вычитание, умножение, деление}, множество корней квадратного уравнения X: X={2, 3}.

Согласно определению, во множестве не бывает одинаковых элементов. Поэтому запись {2, 2, 3} считается некорректной. Ее необходимо заменить на следующую {2, 3}. Порядок следования элементов во множестве роли не играет. Поскольку {2, 3, 4} и {4, 3, 2} состоят из одних и тех же элементов, они задают одно и то же множество. Второй способ задания состоит в том, что мы указываем условие, по которому выбираем эти и только эти элементы во множество, признак, характеризующий все элементы множества. Такой способ называется описательным. В этом случае для задания множества X c элементами x применяется следующая запись: X={x | признак}. Например, X={x | }, А={a | a – день недели}, В={b | b – арифметическое действие}. Описательный способ задания множества напрямую связан с алгеброй высказываний, так как записываемый признак и есть высказывание, касающееся элементов рассматриваемого множества.

Множества можно разделить на конечные и бесконечные.

Конечным множеством называется такое множество, состоящее из конечного числа элементов.

Множество называется бесконечным, если оно состоит из бесконечного числа элементов.

К конечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустым и обозначают Æ. Необходимость его введения вызвана тем, что, определяя множество с помощью некоторого условия, мы не всегда можем сказать заранее, содержит ли оно элементы или нет.

Если каждый элемент множества В является также и элементом множества А, то говорят, что множество В называется подмножеством множества А.

Обозначатся это следующим образом: В Í А (В включено в А).

Подмножество В может и совпадать с множеством А, т.е. множества А и В будут состоять из одних и тех же элементов. В этом случае множества А и В называются равными: А=В (интуитивный принцип объемности).

Если в множествах А и В отличаются хотя бы одним элементом, то А¹В.

Можно заметить, что само множество А является подмножеством самого себя:

А Í А.

Кроме того, пустое множество, по определению, считают подмножеством любого множества:

Æ Í А.

Все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого множества I, т.е. для любого множества А

А Í I.

В этом случае множество I называют универсальным множеством. Например, для алгебры универсальным множеством является множество действительных чисел.

Таким образом, у любого множества обязательно существуют хотя бы два подмножества: пустое множество и само множество. Эти два подмножества называются несобственными подмножествами. Любое подмножество, отличное от несобственного, называется собственным подмножеством данного множества.

Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается P(A). Например, для А={2, 3} множество-степень P(A)={А, {2}, {3}, Æ}, для А={1,2,3} множество-степень таково: P(A)={А, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, Æ}. Название «множество-степень» исходит из того, что число всех подмножеств n-элементного множества равно . Продемонстрируем данный результат. Множество, состоящее из одного элемента а, имеет два подмножества: Æ и {a}. Множество, состоящее из двух элементов а и b, имеет уже 4 подмножества: те же Æ и {a} и еще {b}, {a, b}. Добавим третий элемент с. Множество {a, b, c} кроме рассмотренных выше 4 подмножеств Æ, {a}, {b}, {a, b} имеет еще 4 подмножества {c}, {a, c}, {a, b}, {a, b, c}.Таким образом, ясно, что каждый раз прибавление еще одного элемента ведет к удвоению числа подмножеств. И множество, состоящее из n-элементов, имеет подмножеств.

Операции над множествами

Можно производить новые множества путем применения к исходным множествам определенных операций. Изучение операций над множествами составляет предмет алгебры множеств, имеющей много общего с обыкновенной алгеброй чисел, но и отличающейся от нее в некоторых случаях.

Объединение множеств

Объединением множеств А и В называется множество С, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств А или В, т. е. принадлежат А, или принадлежат В, или принадлежат и А и В. Объединение множеств А и В обозначается через АÈВ. Таким образом,

С=АÈВ={cïcÎA или сÎВ}.

Напомним, что согласно «определению» множества, если один и тот же элемент содержится и в множестве А и в множестве В, то в их объединение этот элемент включается только один раз.

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АÈВ={1, 2, 3, 4, 5, 6, 7}. Если А – множество отличников группы, а В – множество хорошистов, то АÈВ составляет множество и отличников, и хорошистов. Если А – множество отличников группы, а В – все множество студентов группы, то элементами АÈВ являются все студенты группы.

По аналогии с алгеброй чисел объединение иногда называют суммой множеств.

Операции с множествами удобно иллюстрировать при помощи графических схем, в которых отдельные множества представляются в виде кругов. Предполагается, что элементами множества являются все точки круга. Такие круги называются диаграммами Вена или кругами Эйлера.

Если А – множество точек левого круга, а В – точек правого круга на рис.2.1, то заштрихованная фигура есть АÈВ.

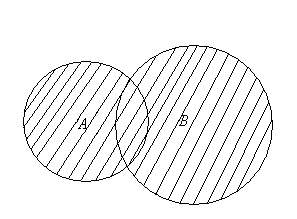
Рис. 2.1

Операция «объединение» аналогичным образом распространяется и для трех, четырех и вообще n множеств , , …, . Множество С= È È…È – это множество, состоящее из всех тех и только тех элементов, которые принадлежат хотя бы одному из множеств , , …, .

Например, если А – множество успевающих студентов группы, В – множество юношей, а С – множество неуспевающих девушек, то АÈВÈС - множество всех студентов группы.

Из определения операции объединение следует, что она обладает многими теми же свойствами, что и операция сложения чисел:

АÈВ = ВÈА – коммутативность (переместительность);

(АÈВ)ÈС = АÈ(ВÈС) – ассоциативность (сочетательность).

Однако объединение множеств обладает и такими свойствами, которыми не обладает сложение чисел:

АÈА = А – закон идемпотентности;

если АÍВ, то АÈВ = В.

Например, если А={2, 4}, а В={1, 2, 3, 4, 5}, то АÈВ={1, 2, 3, 4, 5}. Если А – множество успевающих студентов группы, В – множество успевающих юношей, то АÈВ – по прежнему множество успевающих студентов.

Пересечение множеств

Пересечением множеств А и В называется множество С, состоящее из элементов, которые принадлежат как множеству А, так и множеству В одновременно. Объединение множеств А и В обозначается через АÇВ. Таким образом,

С=АÇВ={cïcÎA и сÎВ}.

Т.е. пересечение множеств есть общая часть данных множеств.

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АÇВ={2, 4}. Если А – множество отличников группы, а В – множество юношей, то АÇВ составляет множество юношей-отличников.

По аналогии с алгеброй чисел пересечение называют произведением множеств.

С помощью кругов Эйлера пересечение множеств А и В изображается следующим образом (заштрихованная часть на рис. 2.2.).

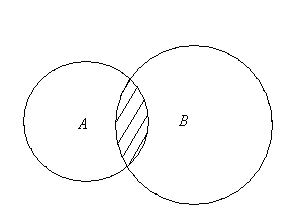
Рис. 2.2

Операцию «пересечение» можно аналогичным образом распространить и на n множеств , , …, . Множество С= Ç Ç…Ç – это множество, состоящее из элементов, которые принадлежат одновременно всем множествам , , …, .

Рассмотрим такой пример. Если А – множество отличников группы, а В – множество неуспевающих студентов, то АÇВ – пустое множество.

Если АÇВ=Æ, то множества А и В называются непересекающимися (Рис. 2.3).

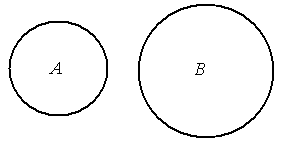
Рис. 2.3

В противном случае, т.е. если АÇВ¹Æ, множества А и В пересекаются.

Операция пересечения множеств обладает многими свойствами операция умножения чисел:

АÇВ = ВÇА – коммутативность (переместительность);

(АÇВ)ÇС = АÇ(ВÇС) – ассоциативность (сочетательность);

(АÈВ) ÇС = (АÇС) È (ВÇС) – дистрибутивность (распределительность).

Укажем такие свойства операции пересечения множеств, которыми операция умножения чисел не обладает:

АÇА=А – идемпотентность;

Если АÍВ, то АÇВ=А. Например, если А={2, 4}, а В={2, 4, 6, 7}, то АÇВ={2, 4}. Если А – множество отличников группы, а В – все множество студентов группы, то АÇВ – множество отличников группы. Данная ситуация представлена на рис.2.4. с помощью кругов Эйлера.

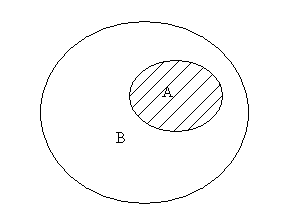
Рис. 2.4

Разность множеств

В отличие от объединения и пересечения множеств эта операция определяется только для двух множеств. Разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат множеству А, но не входят в множество В. Разность множеств А и В обозначается через А\В. Таким образом,

С=А\В={cïcÎA и сÏВ}.

Например, если А={1, 2, 3, 4, 5}, а В={2, 4}, то А\В={1, 3, 5}. Если А – множество отличников группы, а В – множество юношей, то А\В составляет множество девушек-отличников.

С помощью кругов Эйлера для случаев, изображенных на рис.2.5, разность множеств А и В изображается следующим образом (заштрихованная часть).

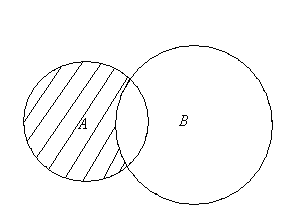
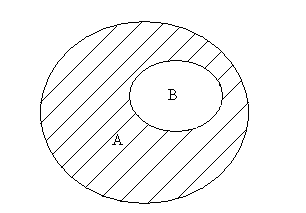
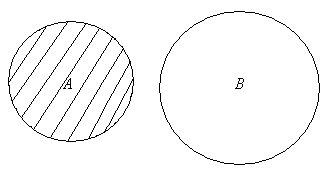
Рис. 2.5

Заметим, что разность множеств не является ни коммутативной, ни ассоциативной операцией.

Симметрическая разность множеств

Симметрической разностью множеств А и В называется множество С, состоящее из элементов, которые принадлежат какому-то одному из множеств А или В. Симметрическая разность множеств А и В обозначается через АDВ.

С=АDВ= (А\В)È (В\А).

Например, если А={1, 2, 3, 4, 5}, а В={2, 4, 6, 7}, то АDВ={1, 3, 5, 6, 7}. Если А – множество отличников группы, а В – множество юношей, то А\В составляет множество девушек-отличников и юношей-неотличников.

С помощью кругов Эйлера симметрическая разность множеств А и В АDВ изображается следующим образом (заштрихованная часть на рис. 2.6).

Рис. 2.6

В отличие от разности множеств симметрическая разность является коммутативной, ассоциативной и дистрибутивной операцией:

АDВ = ВDА – коммутативность (переместительность);

(АDВ)DС = АD(ВDС) – ассоциативность (сочетательность);

(АDВ)ÇС = (АÇС) D (ВÇС) – дистрибутивность (распределительность).

Декартово произведение множеств

Кортеж – это конечный упорядоченный набор объектов произвольной природы, среди которых могут быть и одинаковые. Элементы кортежа заключаются в угловые скобки.

Например: <a, b, c>; <1, 2, 3, 2>; <март, апрель, май>.

В кортеже важен не только состав, но и порядок следования элементов. Например, кортежи <a, b, c, d> и <d, c, b, a> не равны друг другу.

Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств.

Пусть A и B - множества. Выражение вида <a, b>, где aA и bB, называется упорядоченной парой. Равенство вида <a, b> = <c, d> означает, что a=c и b=d.

В общем случае, можно рассматривать упорядоченную n-ку <a1, a2, …, an> из n элементов a1A1, …, anAn. Упорядоченные n-ки иначе называют наборы или кортежи.

Декартовым (прямым) произведением двух множеств А и В называется множество всевозможных упорядоченных пар вида <a, b>, где aA и bB:

A  B = {<a, b> | aA & bB}.

Например, если A = {a, b}, B = {c, d}, то декартово произведение

A  B = {<a,c>, <a,d>, <b,c>, <b,d>}.

Декартовым произведением множеств A1, A2, …, An называется множество упорядоченных n-ок (наборов, кортежей) вида

A1A2…An = {<a1, a2, …, an> | ai  Ai}

Степенью декартового произведения A1A2…An называется число множеств n, входящих в это декартово произведение.