Логические выражения

Прежде чем перейти к рассмотрению ветвящихся и циклических алгоритмов, рассмотрим понятие логического выражения.

В некоторых случаях выбор варианта действий в программе должен зависеть от того, как соотносятся между собой значения каких-то переменных.

Например, расчет корней квадратного уравнения производится по-разному, в зависимости от знака дискриминанта (вспомните школьный курс математики).

В результате сравнения значений двух выражений возможны два варианта ответа: сравнение истинно или ложно.

Например:

2 + 3>3+1— да (истинно)

0 < —7? — нет (ложно)

Выражения такого вида мы будем называть логическими выражениями.

Нам известны шесть операций сравнения:

Знак	Операция
<	Меньше
>	Больше
<=	Меньше или равно
>=	Больше или равно
=	Равно
<>	Не равно

С помощью этих операций мы будем составлять логические выражения. Причем в выражениях присутствуют не только константы, но и переменные.

Часто встречаются задачи, в которых используются не отдельные условия, а совокупность связанных между собой условий (отношений). Например, в магазине вам нужно выбрать туфли, размер которых г = 45, цвет col = белый, цена price не более 400 руб.

Другой пример: школьник выяснил, что сможет купить плитку шоколада, если она стоит 3 руб. или 3 руб. 50 коп.

В первом примере мы имеем дело с тремя отношениями, связанными между собой союзом «и» и частицей "не", во втором — с двумя отношениями, связанными союзом «или». Подобные условия назовем составными и для их обозначения в алгоритме договоримся использовать союзы «и», «или» и частицу «не», которые будем выделять жирным шрифтом и рассматривать как знаки логических операций, позволяющих из простых условий создавать составные, подобно тому как из простых переменных и констант с помощью знаков «+», «—» и т. д. можно создавать алгебраические выражения.

Так, условия наших примеров в алгоритме могут выглядеть следующим образом:

первое: (r = 45) и (col = белый) и (не (price > 400));

второе: (цена = 3) или (цена = 3,5).

Алгоритмы ветвящейся структуры

Алгоритмом ветвящейся структуры будем называть такой алгоритм, в котором выбирается один из нескольких возможных путей (вариантов) вычислительного процесса.

Каждый подобный путь называется ветвью алгоритма.

Признаком разветвляющегося алгоритма является наличие операций условного перехода, когда происходит проверка истинности некоторого логического выражения (проверяемое условие) и в зависимости от истинности или ложности проверяемого условия для выполнения выбирается та или иная ветвь алгоритма. Алгоритм предполагает выполнение Действия 1, если записанное условие истинно (выполняется), и выполнение Действия 2, если условие ложно (не выполняется).

В частном случае может отсутствовать один из блоков — «Действие 1» или «Действие 2».

Пусть, например, В — проверяемое условие, a s1, s2 — некоторые выполняемые инструкции (действия). Тогда:

если условие В выполняется (истинно), то

выбрать для исполнения s1, иначе

выбрать для исполнения s2.

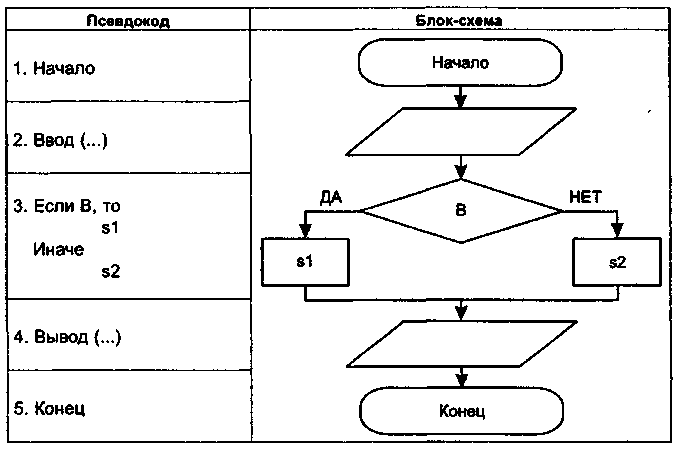
Запишем ветвящийся алгоритм на псевдокоде и графически:

Существуют задачи, связанные с вычислением функций, заданных несколькими арифметическими выражениями (формулами). Приведем пример такой задачи.

Пример 2

Вычислить значение У по одной из формул:

Решение

Исходные данные: х.

Результат: Y.

Метод решения задачи: необходимо выявить область, которой принадлежит значение х, для этого достаточно проверить заданные условия по порядку. Запишем алгоритм в псевдокодах:

Алгоритм

Переменные х, у: вещественные;

Начало

Ввод (х);

Если х < 10, то у : = х + 2;

иначе у : = х - 2;

Вывод (у); Конец.

К задачам рассмотренного выше вида очень часто сводятся вполне реальные задачи, например расчет стипендии, если известно среднее арифметическое оценок студента за месяц. Стипендия отличника равна 100 руб., хорошиста (5 < SJR<4) — 80 руб., остальные стипендию не получают.

Математическая формула:

т. е. мы пришли к задаче вычисления функции по разветвляющемуся алгоритму.

Еще один распространенный вид задач — логические. К ним относятся задачи определения минимума, максимума некоторого числа величин, задачи упорядочивания и сортировки данных и др. Это достаточно сложные задачи, однако в простейших случаях при небольшом числе данных они приводят к построению несложных алгоритмов разветвляющейся структуры. Рассмотрим примеры подобных задач.

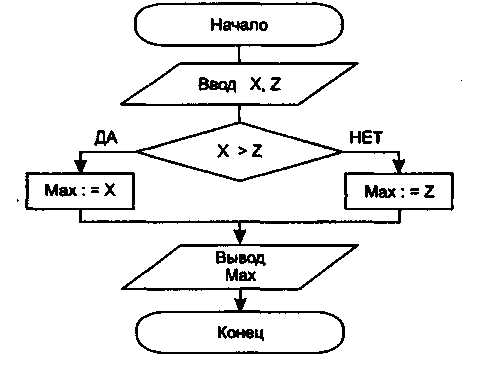
Пример 3

Найти максимальное из двух чисел X, Z. Решение

Исходные данные: X, Z.

Результат: Мах.

Метод решения задачи: нужно сравнить два числа и сделать вывод. Блок-схема алгоритма решения этой задачи выглядит следующим образом: