3.1 Сурет – Графты құру сұлбасы

3.1-кесте

Түйіндер нөмірлері	Студенттік билет нөмірінің соңғының алдындағы цифрасы
	1	2	3	4	5	6	7	8	9	0
i	1	2	1	2	1	4	4	6	6	6
	Студенттік билет нөмірінің соңғы цифрасы
j	1	2	3	4	5	6	7	8	9	0
	2	5	3	6	6	2	6	1	4	2

Есептеу:

1. Құрылымдық матрицасын құру

G=(X,U) граф берілген, мұндағы X – бүтін сандармен белгіленген шыңдар көпшілігі,

Х= {1,2,…,N};

U – латын әріптермен белгіленген қабырғалар көпшілігі;

U= {a,b,c,…,z}.

Құрылымдық матрица квадрат кестесі ретінде ұсынылады, жолдары мен бағаналар шыңдарға сәйкес болады, кірістер келесі шарттар бойынша анықталады:

Берілген граф бойынша құрылымдық матрицасн құрайық.

	1	2	3	4	5
1	1	а	b	с	0
2	0	1	n	0	d
3	0		1	m	0
4		0		1	x
5	0	0	0	0	1

2. УК_i коммутация түйінінен УК_j түйініне дейін барлық мүмкін жолдарын табу.

Бұл үшін матрицаның i-бағана мен j- жолын өшіріп шығарылған анықтағышты математикалық логика заңдары бойынша есептейміз.

Мысал үшін бірінші шыңдан бесінші шыңына мүмкін жолдарын құрайық. Құрылымдық матрицаның бірінші бағана мен бесінші жолын өшіріп шығарылған минорды анықтағыш түрінде жазайық.

3. Граф шыңдар арасындағы белгіленген ранг бойынша жолдар көпшілігін құру.

Барлық белгіленген ранг n бойынша құрылымдық сұлбасын n-деңгейіне тұрғызу қажет. Мысал үшін r2 рангтың барлық жолдарын есептейік. Барлық диагональдық элементтер В² бірлікке тең.

- 2 аспайтын ранг үшін 1 және 2 шыңдар

арасындағы жолдар:

элементті есептеу үшін бірінші жолды үшінші бағансына көбейту қажет.

- 1 және 3 шыңдар

арасындағы жолдар.

- 1 және 4 шыңдар арасындағы жолдар.

- 1 және 5 шыңдар арасындағы жолдар.

Матрицаның екінші жолдың элементтерін В² шығару үшін екінші жолды барлық бағаналарға көбейтеді.

Аналогия бойынша есептер шығарып екіден аспайтын рангпен барлық жолдар матрицасын шығарамыз.

Матрицаны үшінші деңгейіне тұрғызып, яғни В²хВ, ранг үштен аспайтын барлық жолдарын табамыз (яғни 1,2,3 ранг жолдары).

Жолдардың максималды ранг N-1 аспайды, мұндағы N- графтың шыңдар саны.

МОДУЛЬ 2 – «ТЕЛЕФОН ЖЕЛІЛЕРІ»

Тәжірибелік жұмыс №4

ПРИМ ӘДІСІ БОЙЫНША ОРТАЛЫҚТАНДЫРЫЛҒАН

ЖЕЛІЛЕРДІ СИНТЕЗДЕУ

Берілген әдіс S₀ (орталық өңдеу құрылғысына) немесе S_j шыңына жақын, S₀ желісіне қосылған шыңды таңдау идеясына негізделген.

Әрбір S_j шыңына w_j белгісі беріледі, және есептеу басында w₀=0, w_j=- , яғни желіге тек қана S₀ шыңы кіреді.

0-қадам. Т= {t_ij} көпшілігі есептеледі.

w_j=0 болатын шыңдары үшін t_ij= C_ij- w_j.

Соңғы мәндер тек қана C_i0 құнына тең t_i0-ге ие (себебі, w₀=0), ал қалған барлық мәндер тең. Ары қарай Ежи-Вильямс әдісіндегі қадамдар орындалады.

1-қадам. t_ij-дің ең аз мәні анықталады, яғни S₀-ге жақын (1 интерация-сында) S_i шыңы.

{ t_ij}= t_kj

2-қадам. Тексерулер орындалады:

a_k>0 a_k<r_kj

a_k+a_j<r_j0

3-қадам. Келесі мәндер есептеледі:

a_k^н=0 a_j^н=a_j+a_k

r_kj^н=r_ij-a_k F^’=F⁰+C_kj

w_k=0 деп алынады.

Келесі интерацияның 0-қадамына ауысу.

Мысал:

Жоғарыда суреттелген алгоритмді мысалмен көрсетейік. w₀=0 болсын, ал w_j=- . 3-кестедегі мәліметтерді ескере отырып t_ij мәндерін есептейміз.

0-қадам.

Т: t₁₀= C₁₀- w₀=1-0=1

t₂₀= C₂₀- w₀=4-0=4

t₃₀= C₃₀- w₀=3-0=3

t₁₂= C₁₂- w₂=2+ w₂= , t₁₃= ;

t₂₁= C₂₁- w₁=3+ w₁= , t₂₃= _;

t₃₁= C₃₁- w₁=1+ w₁= _; t₃₂= _.

1-қадам. min{tij}-ді анықтаймыз.

min{t_ij}= t₁₀=1

2-қадам. а₁=2>0; r₁₀=5; a₁<r₁₀.

Шарттың орындалуы 3-қадамға өтуге мүмкіндік береді.

3-қадам. Жаңа мәндерді есептейміз:

а¹₁=0; a¹₀=-8+2=-6; r¹₁₀=5-2=3; F=C₁₀=1.

w₁=0; t₁₀= _{қойып, 0-қадамға өтеміз.}

0-қадам. Есептейміз:

Т¹: t₂₁= C₂₁- w₁=3-0=3_;

t₃₁= C₃₁- w₁=1-0=1.

1-қадам. min{TUT¹}= t₃₁, т.е. S₃=>S₁.

2-қадам. а₃=3>0; r₃₁=5>a₃; a₁¹+a₃=0+3 r₁₀=3.

3-қадам. a₃¹=0; a₀¹¹=-6+3=-3.

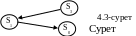
r₁₀¹¹=3-3=0.

r₃₁¹=5-3=2.

F¹=F=C₃₁=1+1=2

w₃=0; t₃₁= _{қойып, 0-қадамға өтеміз.}

0-қадам.

Т²: t₂₃=С₂₃- w₃=1.

1-қадам. min{TUT¹ UT²}= min{t_ij}=t₂₃ анықтаймыз.

2-қадам. а₂=3>0; r₂₃=5>a₂; r₃₁¹=2<a₂, сәйкесінше S₂=>S₃ қосылуы мүмкін емес, t₂₃= қойып, 1-қадамға өтеміз.

1-қадам.min{TUT¹ UT²}= t₂₀=2.

2-қадам. а₂=3>0; r₂₀=5>а₂.

3-қадам. . а₂¹=0; r₂₀¹=5-3=2; а₀¹¹¹=-3+3=0

F=2+4=6

Барлық а_i¹=0 болғандықтан, тапсырма шешімі табылды.

4.4- сурет

№ 5 Тәжірибелік жұмыс