Задачи и упражнения

5.42. Вычислить поток векторного поля через полную поверхность треугольной пирамиды с вершинами: О(0; 0; 0), А(1; 0; 0), В(0; 1; 0) и С(0; 0; 1).

5.43. Вычислить поток векторного поля 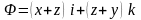через полную поверхность цилиндра, ограниченного поверхностями: , , .

5.44. Вычислить поток векторного поля 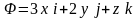через полную поверхность сферы .

С помощью формулы Остроградского-Гаусса вычислить следующие поверхностные интегралы:

5.45. Где ∑- внешняя сторона поверхности куба

5.46. где ∑ - наружная сторона пирамиды, ограниченной поверхностями

5.47. где ∑- внешняя сторона сферы

Вычислите циркуляцию векторного поля по замкнутому контуру . Проверьте результат при помощи формулы Стокса.

5.48. , .

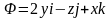5.49. , , .

5.50. , где – линия пересечения плоскости 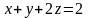с координатными плоскостями , , .

6. Контрольные вопросы

1. Какая плоская (пространственная) кривая называется: а) простой незамкнутой (замкнутой); б) спрямляемой; в) гладкой; г) кусочно-гладкой?

Приведите примеры.

2. Напишите параметрические уравнения плоской кривой, заданной: а) в декартовых координатах; б) в полярных координатах. Приведите примеры таких кривых.

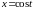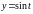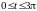3. Является ли кривая , , , простой? Является ли кривая , , 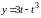, гладкой, кусочно-гладкой?

4. Сформулируйте определения: а) интегральных сумм для криволинейного интеграла первого рода; б) предела этих интегральных сумм; в) криволинейного интеграла первого рода.

5. Зависит ли от направления обхода кривой: а) криволинейный интеграл первого рода; б) какая-нибудь его интегральная сумма?

6. Какие физические приложения криволинейного интеграла первого рода вы знаете?

7. Сформулируйте определения: а) интегральных сумм для криволинейного интеграла первого рода; б) предела этих интегральных сумм; в) криволинейного интеграла первого рода.

8. Напишите формулы, выражающие линейность и аддитивность криволинейных интегралов по длине дуги.

9. Напишите формулы для вычисления криволинейных интегралов по длине дуги.

10. Дайте определение криволинейного интеграла второго рода. Какая связь между криволинейными интегралами первого и второго рода?

11. Напишите формулы для вычисления криволинейных интегралов второго рода.

12. Зависит ли от направления обхода кривой криволинейный интеграл второго рода. Какое направление обхода замкнутой кривой принимают за положительное? В каком случае интеграл по замкнутой кривой равен нулю?

13. Как вычисляется работа векторного поля? Что называется циркуляцией векторного поля и каков её физический смысл?

14.Какое векторное поле называется потенциальным? Сформулируйте четыре теоремы о свойствах потенциальных векторных полей.

15. Дайте определение предела интегральных сумм и двойного интеграла. Докажите, что неограниченная в области функция не интегрируема в этой области.

16. Что называется диаметром ограниченного множества точек? Чему равен диаметр: а) квадрата со стороной 1; б) области, ограниченной эллипсом ?

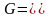
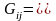
18. Что такое интегральная сумма для функции двух переменных? Составьте интегральную сумму функции , соответствующую разбиению области на прямоугольники и выбору левых верхних вершин этих прямоугольников в качестве

19. Напишите формулы, выражающие линейность и аддитивность двойных интегралов.

20. Сформулируйте геометрический смысл двойного интеграла. Как вычислить объем тела и площадь плоской области с помощью двойного интеграла?

21. Сформулируйте теоремы и следствия о вычислении двойных интегралов.

22. Сформулируйте теорему о замене переменных в двойном интеграле. Напишите формулу перехода к полярным координатам.

23. Сформулируйте теорему о формуле среднего значения для двойного интеграла, аналогичную теореме для определенного интеграла.

24. Сведите двойной интеграл 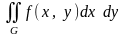к повторному интегралу двумя способами, если G – круг, ограниченный окружностью .

25.Сформулируйте теорему Грина и следствия к ней.

26. Дайте определение предела интегральных сумм и тройного интеграла. Докажите, что неограниченная в пространственной области функция не интегрируема в этой области.

27. Напишите формулы, выражающие линейность и аддитивность тройных интегралов.

28. Сформулируйте теорему о сведении тройного интеграла к повторному, в котором внутренний интеграл является определенным интегралом.

29. Сформулируйте теорему о формуле среднего значения для тройного интеграла.

30. Напишите формулы перехода в тройном интеграле от прямоугольных координат 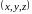к цилиндрическим ( сферическим координатам. Вычислите якобианы перехода. Что представляет собой координатные поверхности z=const, , , 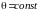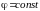и координатные линии z, ?

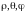31. Сформулируйте понятие векторного поля. Дайте определение дивергенции векторного поля в инвариантном виде. Теорема об её вычислении в декартовой системе координат.

32. Запишите свойства дивергенции. В чем состоит её физический смысл?

34. Дайте определение соленоидального векторного поля. Приведите примеры таких полей. Если поле является соленоидальным в области, то чему будет равен поток через замкнутую поверхность, лежащую в этой области?

35. Сформулируйте четыре свойства соленоидального векторного поля, а также необходимое и достаточное условия соленоидальности.

36. Дайте определение предела интегральных сумм и поверхностного интеграла первого рода. Докажите, что неограниченная на поверхности функция не интегрируема на этой поверхности.

37. Напишите формулы, выражающие линейность и аддитивность поверхностного интеграла первого рода.

38. Запишите формулы вычисления поверхностного интеграла первого рода при различных способах задания поверхности

39. Дайте определение поверхности: а) двусторонней; б) односторонней; в) ориентируемой. Приведите примеры. Зависит ли от ориентации поверхностный интеграл 1 рода?

40. Дайте определение поверхностного интеграла 2 рода и напишите формулы для его вычисления в зависимости от способа задания поверхности. Зависит ли от ориентации поверхностный интеграл 2 рода?

41. Что называется потоком векторного поля через поверхность? Приведите примеры физических полей. Как вычисляется поток?

42. Дайте определение ротора векторного поля в инвариантной форме и запишите формулу для его вычисления в декартовой системе координат. Каков физический смысл ротора? Приведите примеры безвихревых полей.

43.Дайте определение поверхностно односвязанной области в пространстве, приведите примеры. Сформулируйте теорему Стокса. Каков физический смысл формулы Стокса?

44.Какое векторное поле называется потенциальным? Приведите примеры потенциальных полей. Сформулируйте необходимое и достаточное условия потенциальности векторного поля.

45. Что такое оператор Гамильтона? Запишите с помощью оператора Гамильтона: а) градиент скалярного поля; б) дивергенцию векторного поля; в)ротор векторного поля.