3. Тройной интеграл
3.1.Вычисление
тройного интеграла в декартовой системе
координат.
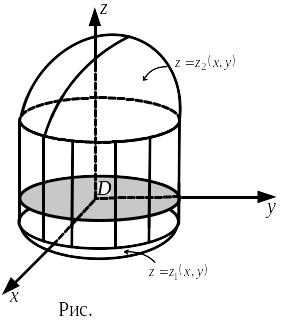
Пусть функция трех переменных
определена и непрерывна в пространственной
области
,
которая ограничена сверху поверхностью
,
а снизу – поверхностью
.
Функци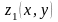и
и
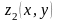определены и непрерывны в области
(рис. 3.1). Тогда вычисление тройного
интеграла сводится к последовательному
(справа налево) вычислению определенного
интеграла по переменной
(переменные
и
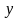считаются при этом константами) и
двойного интеграла от того, что получится,
по области
.
.
В
частности, если область
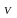представляет собой прямоугольный
параллелепипед, определяемый неравенствами
,
,
,
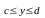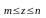то тройной интеграл сводится к трем
определенным интегралам:
.
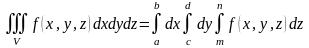Естественно, можно выбирать другой порядок интегрирования.
Если подынтегральная функция равна единице, т.е. f(x,y,z)=1, то тройной интеграл равен объему тела V.
Пример 1. Вычислить тройной интеграл:
.
Решение.
Пример 2.
Вычислить тройной интеграл
,
если область
ограничена плоскостями:
.
Решение. Построим область (рис. 3.2) и ее проекцию на плоскость (рис. 3.3):
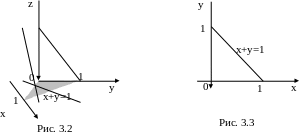
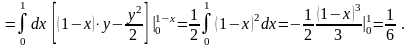
Задачи и упражнения
Вычислить тройные интегралы:
3.1.
.
3.2.
.
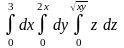3.3.
.
3.4.
;
область
ограничена
плоскостями
.
3.5.
;
область
ограничена плоскостями
.
3.6.
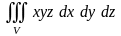; область
ограничена плоскостями
и сферой
.
3.7.
;
область
ограничена плоскостями
и цилиндром
.
3.8.
3.9.
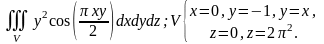
3.10.
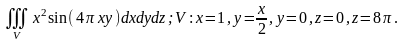
3.11.
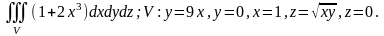
3.12.
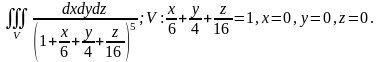
3.13.
3.2.
Замена переменных в тройном интеграле.
Часто при
вычислении тройных интегралов
целесообразно использовать цилиндрическую
или сферическую системы координат.
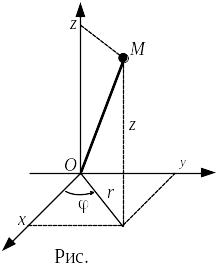
Цилиндрические координаты
,
,
(рис. 3.4) представляет собой обобщение
полярных координат на плоскости и
связаны с прямоугольными координатами
,
,
формулами
,
,
.
Переход к тройному интегралу в цилиндрических координатах осуществляется по формуле
.
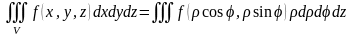В
частности, если положить в этом равенстве
,
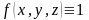то получим формулу для объема тела в
цилиндрических координатах:
.
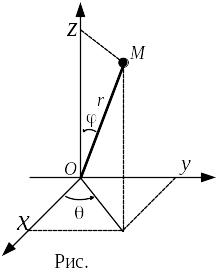
Сферические
координаты
,
,
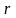связаны с прямоугольными координатами
,
,
при помощи формул (рис. 3.5)
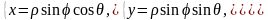
В
общем случае переменные
,
,
изменяются в пределах
,
,
.
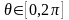Формула перехода к сферическим координатам
имеет вид
.
Положив , получим формулу для объема тела в сферических координатах.
Пример 3. Вычислить тройной интеграл с помощью перехода к цилиндрическим координатам:
.
Решение.
Построим область
(рис. 3.6) и ее проекцию на плоскость
(рис. 3.7).
→ 
.
Тогда, получим:
Задачи и упражнения
Вычислить тройные интегралы:
3.14.
.
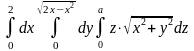3.15.
;
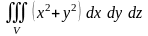область
ограничена плоскостью
и параболоидом
.
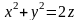3.16.
;
область
ограничена плоскостью
и сферам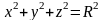и
и
.
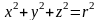3.17.
;
область
ограничена плоскостями
и цилиндром
.
Вычислить объемы тел, ограниченных следующими поверхностями:
3.18. Плоскостями и параболоидом .
3.19. Плоскостями и цилиндром .
3.20. Плоскостями и цилиндром .
3.21. Плоскостями
3.22.
3.23.
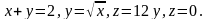
3.23.
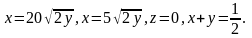
3.24.
3.25.
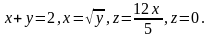
3.26.
3.27.
3.28.
3.29.
3.30.
3.31.
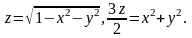
3.32.
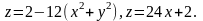
3.33.
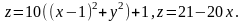
3.34.
3.35.
