
- •Часть 3
- •1. Криволинейные интегралы
- •2. Двойной интеграл
- •2.1. Двойной интеграл в декартовой системе координат. Пусть область можно задана системой неравенств (рис.2.1):
- •3. Тройной интеграл
- •4. Поверхностные интегралы
- •5. Элементы векторного анализа
- •Задачи и упражнения
- •Вычислим ротор поля 𝚽: rot𝚽
- •Задачи и упражнения
- •5.45. Где ∑- внешняя сторона поверхности куба
- •6. Контрольные вопросы
М инистерство
образования Российской Федерации
инистерство
образования Российской Федерации
Южно-Российский государственный технический университет
(Новочеркасский политехнический институт)

ЗАДАЧИ И УПРАЖНЕНИЯ
ПО КУРСУ
«МАТЕМАТИЧЕСКИЙ АНАЛИЗ»
Часть 3
КРИВОЛИНЕЙНЫЕ И КРАТНЫЕ ИНТЕГРАЛЫ
Новочеркасск 2013
УДК 512
Рецензент: доктор физико-математических наук, профессор А. Э. Пасенчук
Составители: Никифоров А.Н., Власов М. В.
Задачи и упражнения по курсу «Математический анализ»: Методическое пособие. Ч. 3. Криволинейные и кратные интегралы / Юж.-Рос. гос. техн. ун-т. Новочеркасск: ЮРГТУ (НПИ), 2013.
Сборник содержит задачи и упражнения для проведения практических занятий, предусмотренных учебным планом по курсу «Математический анализ» для бакалавров, обучающихся по направлению «Прикладная математика. Может быть использован студентами других специальностей при изучении соответствующих разделов высшей математики.
Южно-Российский государственный технический университет, 2013
Авторы. 2013
1. Криволинейные интегралы
1.1.
Криволинейный интеграл первого рода.
Криволинейный
интеграл первого рода сводится к
определенному интегралу в зависимости
от способа задания кривой. Если кривая
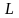 задана непрерывно дифференцируемой
функцией
задана непрерывно дифференцируемой
функцией
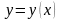 ,
,
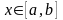 ,
то
,
то
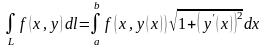 ,
,
при
этом выражение
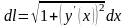 называется дифференциалом
длины дуги.
называется дифференциалом
длины дуги.
Если
кривая
задана параметрически, т.е. уравнениями
 ,
,
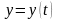 ,
,
где
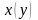 ,
,
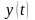 – непрерывно дифференцируемые функции
на некотором отрезке
– непрерывно дифференцируемые функции
на некотором отрезке
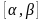 ,
то
,
то
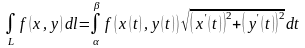 .
.
Если
L
пространственная кривая, заданная
параметрически уравнениями
,
,
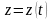 ,
,
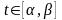 ,
а
,
а
 – непрерывная функция вдоль кривой
,
то
– непрерывная функция вдоль кривой
,
то
 .
.
Если
плоская кривая
задана полярным уравнением
 ,
,
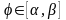 ,
то
,
то
 .
.
Если
подынтегральная функция равна единице,
то криволинейный интеграл от единичной
функции равен длине
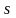 кривой
,
т.е.
кривой
,
т.е.
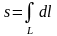 .
.
Пусть
в плоскости
 задана гладкая кривая
,
на которой определена и непрерывна
функция двух переменных
задана гладкая кривая
,
на которой определена и непрерывна
функция двух переменных
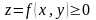 .
Тогда можно построить цилиндрическую
поверхность с направляющей
и образующей, параллельной оси
.
Тогда можно построить цилиндрическую
поверхность с направляющей
и образующей, параллельной оси
 и заключенной между
и поверхностью
и заключенной между
и поверхностью
 .
Площадь этой цилиндрической поверхности
можно вычислить по формуле
.
Площадь этой цилиндрической поверхности
можно вычислить по формуле
 .
.
Если
– материальная кривая с плотностью,
равной
 ,
то масса этой кривой вычисляется по
формуле (физический
смысл криволинейного интеграла первого
рода):
,
то масса этой кривой вычисляется по
формуле (физический
смысл криволинейного интеграла первого
рода):
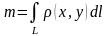 .
.
Пример
1. Вычислить
 ,
где
,
где
 L
-
отрезок прямой, соединяющий точки O(0;
0) и A(1;
2).
L
-
отрезок прямой, соединяющий точки O(0;
0) и A(1;
2).
Решение.
Уравнение OA:
 ;
;
 ;
;
 ;
;
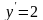
 ;
;
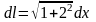 ;
;
 ;
;
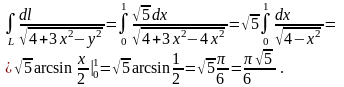
Пример 2.
Вычислить
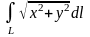 ,
где
‑ контур окружности
,
где
‑ контур окружности
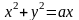 .
.
Решение.
Введем полярные координаты
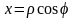 ,
,
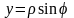 .
Тогда уравнение окружности принимает
вид
.
Тогда уравнение окружности принимает
вид
 ,
для которой
,
для которой
 ;
;
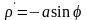 ,
,
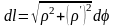 ,
,
 ,
,

Пример 3.
Вычислить
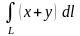 ,
где
‑ четверть окружности
,
где
‑ четверть окружности
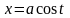 ,
,
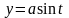 ,
причем
,
причем
 .
.
Решение.
Так как
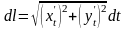 ,
то в нашем случае:
,
то в нашем случае:
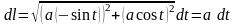 ;
;

Задачи и упражнения
Вычислить следующие криволинейные интегралы первого рода:
1.1.
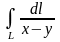 ,
где
– отрезок прямой, соединяющий точки
,
где
– отрезок прямой, соединяющий точки
 и
и
 .
.
1.2.
 ,
где
– отрезок прямой, соединяющий точки
,
где
– отрезок прямой, соединяющий точки
 и
и
 .
.
1.3.
 ,
где
– дуга параболы
,
где
– дуга параболы
 от точки
до точки
от точки
до точки
 .
.
1.4.
,
где L
-
отрезок прямой
 ,
соединяющий точки
A(0;
-2)
и В(4;
0).
,
соединяющий точки
A(0;
-2)
и В(4;
0).
1.5. , где - контур Δ ABO с вершинами A (1; 0),B (0; 1) и O(0; 0).
1.6.
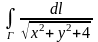 ,
где
,
где
 – отрезок прямой соединяющий точки
– отрезок прямой соединяющий точки
 и
и
 .
.
1.7.
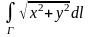 ,
где
– окружность
,
где
– окружность
 .
.
1.8.
 ,
где
-
арка циклоиды
,
где
-
арка циклоиды
 ,
,
 ,
причем
,
причем
 .
.
1.9.
 ,
где
-
окружность
,
где
-
окружность
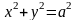 .
.
1.10.
 ,
где
– четверть эллипса
,
где
– четверть эллипса
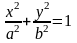 ,
лежащая в первом квадранте.
,
лежащая в первом квадранте.
1.11.
 ,
где
– окружность
,
где
– окружность
 .
.
1.12.
 ,
где
– первый виток винтовой линии
,
,
,
где
– первый виток винтовой линии
,
,
 .
.
1.13.
Найдите длину дуги кривой
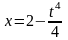 ,
,
 между ее точками пересечения с осями
координат.
между ее точками пересечения с осями
координат.
1.14.
Найдите длину дуги конической винтовой
линии
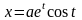 ,
,
 ,
,
 от точки
от точки
 до точки
до точки
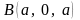 .
Указание: точке
.
Указание: точке
 соответствует значение параметра
соответствует значение параметра
 ,
а точке
,
а точке
 – значение
– значение
 .
.
1.15.
Найдите массу однородной полуарки
циклоиды
,

 .
.
1.16.
Найдите массу дуги
 кривой
кривой
 ,
если в каждой ее точке линейная плотность
пропорциональна квадрату абсциссы
точки, причем
,
если в каждой ее точке линейная плотность
пропорциональна квадрату абсциссы
точки, причем
 ,
,
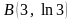 .
.
1.17. Найдите
массу дуги
кривой
,
если в каждой ее точке линейная плотность
пропорциональна квадрату абсциссы
точки (коэффициент пропорциональности
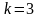 ).
).
 .
.
1.18.
Найдите массу отрезка
прямой, если в каждой ее точке линейная
плотность обратно пропорциональна
абсциссе точки (коэффициент
пропорциональности
 ).
).
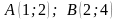 .
.
1.19. Найдите массу отрезка прямой, если в каждой ее точке линейная плотность обратно пропорциональна ординате точки (коэффициент пропорциональности ). .
1.20. Найдите массу
дуги
параболы
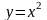 ,
если в каждой ее точке линейная плотность
пропорциональна абсциссе
,
коэффициент пропорциональности
,
если в каждой ее точке линейная плотность
пропорциональна абсциссе
,
коэффициент пропорциональности
 .
.
1.2.
Криволинейный интеграл второго рода.
Предположим,
что плоская кривая
задана в явном виде непрерывно
дифференцируемой функцией
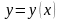 ,
.
Тогда криволинейный
интеграл второго рода сводится
к определенному интегралу по формуле:
,
.
Тогда криволинейный
интеграл второго рода сводится
к определенному интегралу по формуле:
 .
.
Если кривая плоская и задается параметрически функциями , , , то
 .
.
В
пространственном случае, когда функции
P(x,y,z),Q(x,y,z),R(x,y,z)
имеют
координаты
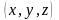 и заданы на кривой L,
криволинейный
интеграл вычисляют по формуле:
и заданы на кривой L,
криволинейный
интеграл вычисляют по формуле:
 ,
,
где
 и
,
,
– параметрические уравнения кривой.
и
,
,
– параметрические уравнения кривой.
Пример
4. Вычислить
 ,
где
-
дуга параболы
от точки A(-1;
1) до точки В(1;
1).
,
где
-
дуга параболы
от точки A(-1;
1) до точки В(1;
1).
Решение.
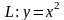 ;
;
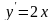 ;
;
 ;
;
 .
.

Пример 5.
Вычислить
 ,
где
‑ отрезок прямой АВ,
от точки A(1;
1; 1) до точки В
(2; 3; 4).
,
где
‑ отрезок прямой АВ,
от точки A(1;
1; 1) до точки В
(2; 3; 4).
Решение. Уравнение АВ:
 ;
;
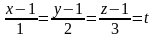 ;
;
 ,
,

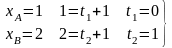 ,
,
 ;
;


Задачи и упражнения
Вычислить следующие криволинейные интегралы второго рода:
1.21.
 вдоль линии: 1)
вдоль линии: 1)
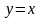 ;
2)
;
;
2)
;
3)
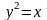 ;
4)
;
4)
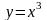 .
.
1.22.
 вдоль линии: 1)
;
2)
;
вдоль линии: 1)
;
2)
;
3) ; 4) .
1.23.
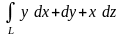 ,
вдоль отрезка прямой АВ, где А(0; 0; 0)
и В(2; 3; 4).
,
вдоль отрезка прямой АВ, где А(0; 0; 0)
и В(2; 3; 4).
1.24.
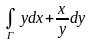 ,
где
– дуга кривой
,
где
– дуга кривой
 от точки
от точки
 до точки
до точки
 .
.
1.25.
 ,
где
– дуга кривой
от точки
до точки
,
где
– дуга кривой
от точки
до точки
 .
.
1.26.
 ,
вдоль окружности
,
вдоль окружности
 ,
,
 и
.
и
.
1.27.
 ,
вдоль линии
,
вдоль линии
 ,
,
 ,
,
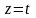 ,
причем
,
причем
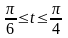 .
.
1.28.
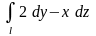 вдоль линии
вдоль линии
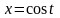 ,
,
 ,
,
причем
,
,
причем
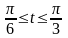 .
.
1.29.
 ,
где
– окружность
,
где
– окружность
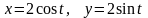 (обход
в положительном направлении).
(обход
в положительном направлении).
1.30.
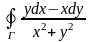 ,
где
– окружность
,
где
– окружность
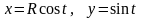 (обход
в положительном направлении).
(обход
в положительном направлении).
1.31.
 ,
где
– верхняя половина эллипса
,
,
где
– верхняя половина эллипса
,
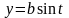 ,
пробегаемая против хода часовой стрелки.
,
пробегаемая против хода часовой стрелки.
1.32.
 ,
где точки
,
где точки
 и
и
 соединены кривой
соединены кривой

1.33.
 ,
где
– длина первой арки циклоиды
,
,
пробегаемая в направлении возрастания
параметра
,
где
– длина первой арки циклоиды
,
,
пробегаемая в направлении возрастания
параметра
 .
.
1.34.
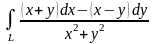 ,
где
– окружность
,
пробегаемая против хода часовой стрелки.
Указание: используйте параметрическое
уравнение окружности.
,
где
– окружность
,
пробегаемая против хода часовой стрелки.
Указание: используйте параметрическое
уравнение окружности.
1.35.
 ,
где
– виток винтовой линии
,
,
,
где
– виток винтовой линии
,
,
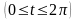 .
.
1.36.
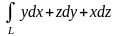 ,
где
– ломаная линия
,
где
– ломаная линия
 с вершинами
с вершинами
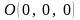 ,
,
 ,
,
 ,
,
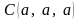 .
.
