Скопировано! Вам двойка!!!

Скопировано. Вам двойка!!!

Z= Скопировано. Вам двойка!!!

4.2.Используя редактор Формул, измените содержимое блоков нижеприведенной блок-схемы (рис.3), так чтобы блок-схема имела более наглядный и правильный вид:

Начало

Z=(Fa+Fb)/2

1

3

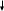
x = a

5

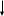
i=1, n-1

6

x =x+ Δx

7

Z=Z+F(х)

8

a, b, n

2

Z=Z * Δx

4

Δx=(b-a)/n

10

9

Zт = p / 2

11

ΔZ=|Zт-Z|*100/Zт

Z, Zт, ΔZ

12

13

Конец

Скопировано. Вам двойка!!!!!

Рис.3. Блок-схема алгоритма для расчета интеграла методом трапеций, созданная без использования редактора Формул

Лабораторная работа №9 Проведение сложных математических расчетов в электронных таблицах.

1.Цель работы

Целью работы является получение навыков в проведении сложных

математических расчетов в электронных таблицах.

2.Контрольные вопросы

2.1.Как организовать операцию цикл в электронных таблицах?

2.2.Как провести выделение несмежного диапазона ячеек таблицы?

2.3.Как рассчитать относительную погрешность вычисления интеграла методом трапеций?

3.Методические указания

3.1.Электронные таблицы создаются с целью проведения сложных математических расчетов. В этих расчетах часто используются тригонометрические функции. Примерами таких функций являются sin (x) и

cos (x).

3.2. Описание метода трапеций.

Более сложные функции рассчитываются итерационными методами.

В качестве расчета сложной функции ниже приведен пример вычисления интеграла методом трапеций. Суть этого метода такова.

Метод трапеций заключается в линейной аппроксимации функции f на отрезке [а; b]. Отрезок [а; b] разбивается на n частей длины .

С учетом суммирования смежных ординат внутри отрезка [а; b] обобщенная формула трапеций для вычисления приближенного значения интеграла имеет вид:

Z= (1)

На рис. 1 показан геометрический смысл этой формулы при n=2. Линейная интерполяция приводит к замене графика функции f ломаной, соединяющей точки (х₀, уо), (х₁, у₁),…,(х_n, у_n) этого графика. Затем вместо криволинейной трапеции рас­сматривают фигуру D, состав­ленную из прямолинейных трапеций с основаниями у_i и у_i+1 и высотой h. Формула (1) означает замену площади

кри­волинейной трапеции площа­дью фигуры D. Площадь фигуры D составляет приближенное значение интеграла.

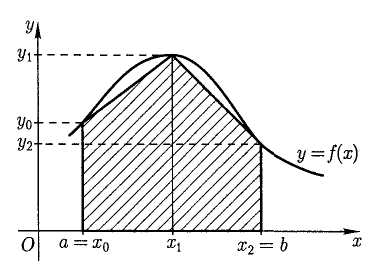
Рис. 1. Графическая интерпретация формулы трапеций для n=2

3.3.Вычисление интеграла методом трапеций

Вычислить на ПЭВМ методом трапеций приближенное значение интеграла

Z=

для а=0; b=; к=0,5, разбивая отрезок интегрирования на n частей.

Для оценки относительной погрешности используемого метода трапеций необходимо знать точное значение интеграла, которое составляет для к ≤ 0,9

Схема алгоритма решения задачи представлена на рис.2. Блок 3 задает начальное значение суммы, равное ; накопление суммы организовано циклически. Перед циклом значению х присваивается значение левого конца интервала интегрирования a. При каждом прохождении цикла в блоке 7 значение х увеличивается на шаг Δx=h, в блоке 8 вычисляется текущее значение ординаты функции f(х) и прибавляется к сумме Z. После выполнения цикла (n-1) раз осуществляется переход к блоку 9, где вычисляется окончательное приближенное значение интеграла. Чтобы оценить точность используемого итерационного метода для вычисления интеграла, в данном случае это метода трапеций, в блоке 10 параметру Zт присваивается точное значение интеграла, а в блоке 11 вычисляется относительная погрешность метода трапеций ΔZ в процентах.

Начало

Z=(Fa+Fb)/2

1

3

x = a

5

i=1, n-1

6

x =x+ Δx

7

Z=Z+F(х)

8

a, b, n

2

Z=Z * Δx

4

Δx=(b-a)/n

10

9

Zт = p / 2

11

ΔZ=|Zт-Z|*100/Zт

Z, Zт, ΔZ

12

13

Конец

Скопировано. Вам двойка!!!!!

Рис.2. Блок-схема алгоритма для расчета интеграла методом трапеций

3.4.Для вычисления интеграла можно было бы написать программу по блок-схеме рис.2 на каком-то языке программирования, например, БЕЙСИК, С++ или ПАСКАЛЬ. Однако это бы было неприятно, а может быть и совсем не возможно для тех, кто плохо владеет программированием или совершенно его не знает, т.к. пришлось бы в срочном порядке осваивать какой–то язык программирования. Однако от этого можно избавиться, если воспользоваться электронной таблицей Excel.

3.5.Ряд операций программирования достаточно легко провести в электронных таблицах. Так, например, для x =x+ Δx операцию «цикл» можно провести следующим образом:

-введите в ячейку формулу, в которой будет содержаться адресная метка на верхнюю ячейку столбца, например, формулу =B2+0,314 в ячейку В3 (таблица 1);

-затем щелкните эту ячейку и переместите указатель мыши в правый нижний угол, при этом указатель мыши превратится в маленькое перекрестие, называемое маркером заполнения;

-нажмите и не отпускайте левую кнопку мыши;

-двигаясь мышью, например, вниз, пока возникающая рамка не охватит столько ячеек, сколько необходимо для шагов (итераций) цикла, например ячейки В4-В11 таблицы 1 для 10 шагов цикла;

-отпустите левую кнопку мыши.

В результате таких действий автоматически занесутся в последующие ячейки В4-В11 недостающие формулы с автоматически измененными адресными данными ячеек.

Аналогичным способом можно организовать циклический расчет Z=Z+f(х) в столбце H таблицы 1.

Остальные расчеты блок-схемы рис.2 достаточно просто выполнить, организуя необходимые формулы в ячейках таблицы, а также пользуясь функциями для расчета SIN (x) и COS (x) и функцией ABS() для нахождения абсолютного значения числа.

Таблица 1. Расчет функций и формул, необходимых для вычисления интеграла по методу трапеции (к=0,5, число шагов итерации 10)

	A	B	C	D	E	F	G	H
1	i	Расчет х	Sin(x)	Cos(x)	Sin(x)^2	Знаменатель	f(x)	Z(х)
2	1	0	=SIN (B2)	=COS(B2)	=C2^2	=1,25+D2	=E2/F2	=(G2+G11)/2
3	2	=B2+0,314	= SIN (B3)	= COS (B3)	=C3^2	=1,25+D3	=E3/F3	=H2+G3
4	3	=B3+0,314	= SIN (B4)	= COS (B4)	=C4^2	=1,25+D4	=E4/F4	=H3+G4
…	…	…	…	…	…	…	…	…
11	10	=B10+0,314	= SIN (B11)	= COS (B11)	=C11^2	=1,25+D11	=E11/F11	=H10+G11

3.6.Создание диаграмм с помощью Мастера диаграмм без использования меток

Обычно электронная таблица, по которой строится диаграмма, должна включать названия столбцов и названия строк, представленных в виде текста или меток. Однако бывают ситуации когда, например, в первом столбце, начиная со второй строки, записаны числовые значения данных по оси Х. Тогда эти числа необходимо превратить в метки, которые не понимают функции, если они использованы в электронной таблице и ссылаются на данные первого столбца. Электронная таблица сообщает об ошибках, которые иногда исправить бывает не возможно. Поэтому возникает необходимость построения диаграмм без использования меток. Такой способ построения включает следующие действия:

-заполните электронную таблицу данными, по которым необходимо построить диаграмму;

-выделите данные для включения в диаграмму по вертикальной оси Y;

-выберите тип диаграммы в группе Диаграммы из вкладки Вставка;

-щелкните подтип диаграммы.

В электронной таблице отобразится диаграмма по выделенным вами данным, причем по оси Х в диаграмме будут проставлены данные 1,2, 3 и т.д. по умолчанию. Для включения данных по горизонтальной оси Х выполните следующие действия:

-щелкните команду Выбрать данные в группе Данные из вкладки Конструктор;

-выберите в Подписи горизонтальной оси (категории) кнопку Изменить;

-выделите мышью диапазон ячеек для подписей оси Х;

-нажмите ОК для подтверждения ввода указанного диапазона;

-щелкните ОК.

Кроме этого, при необходимости с помощью вкладок Макет и Конструктор можно изменять тип, подписи и другие параметры диаграммы.

4.Задание (вариант задания отличается порядковым номером записи фамилии студента в журнале)

4.1.Аналогично с таблицей 1 в электронной таблице проведите расчет функций, требуемых для приближенного вычисления интеграла методом трапеций для к=0,5 плюс ваш порядковый номер в журнале, деленный на 100, разбивая отрезок интегрирования на 10 частей, т.е. n=10. В ячейке F16 произведите окончательный расчет приближенного значения интеграла по формуле =H11*0,314 (блок 9 Рис.2).

4.2.В ячейке F21 рассчитайте относительную погрешность метода расчета в процентах по формуле =ABS(F19-F16)/F19*100 (блок 11 рис. 2), считая, что точное значение интеграла  / 2 или приблизительно 1,57 записано вами в ячейке F19 (блок 10 рис.2).

4.3.Постройте следующие графики:

-SIN (x) и COS (x);

-подынтегральной функции f(x);

-накопительной функции Z(х).

При их построении для оси Х используйте диапазон ячеек B2:B11.

4.4.И наконец-то, используя редактор Формул, создайте непосредственно на ваших расчетах в электронной таблице формулу, для которой Вы производили расчеты:

Z=

для n=10 и к=(укажите значение в соответствии с вашим вариантом).