Розрахункова робота 14 Застосування методу Ньютона для визначення фракційного складу суспензій

М ета роботи: навчитися проводити математичну обробку експериментальних даних для визначення функції розподілу частинок за розмірами, аналізувати здобуті результати.

Як розглядалося раніше, для застосування аналітичних методів обробки експериментальних даних із седиментації потрібне рівняння, яке б описувало криву седиментації. Для тих випадків, коли розподіл частинок за розмірами близький до логарифмічно-нор-мального закону, М. Цюрупою запропоновано підхід, суть якого полягає в тому, що залежність маси речовини, яка осіла в процесі седиментації, від часу можна описати рівнянням , що описує седиментаційну криву. Величину можна знайти диференціюванням цієї функції з подальшим розрахунком за рівнянням (3.16). Кінцевим результатом обробки в обох випадках є залежність , що є інтегральною кривою розподілу маси частинок за розмірами. Далі, диференціюванням рівняння , отримують залежність, що описує диференціальну криву розподілу частинок за розмірами. Використання рівняння М. Цюрупи не завжди можна обґрунтувати, оскільки розподіл частинок суспензії за розмірами може бути будь-яким.

Розглянемо виведення рівняння, яке описує залежність маси речовини, що осіла в процесі седиментації, від часу, яке справедливе для будь-якого розподілу частинок суспензії за розмірами.

Для монодисперсної системи маса осаду Q з часом буде збільшуватись пропорційно до маси частинок, що містяться в шарі суспензії одиничної товщини та швидкості осідання частинок, тобто:

, або ,

де t_і — час повного осідання частинок певного радіуса з висоти H, а — загальна маса монодисперсних частинок. Зрозуміло, що це рівняння справедливе до часу t ≤ t_і.

Виходячи з припущення незалежності руху кожної частинки в полідисперсній системі від інших, можна записати, що для n-дисперсної системи масу осаду з часом можна буде описувати рівнянням:

,

причому тільки за умови t < t_i, а при t > t_i — = const ( — загальна маса частинок і-ї фракції; t_і — час повного осідання частинок певного радіуса з висоти H).

Указані умови будуть виконані, якщо рівняння записати так:

. (5.6).

Тоді при t < t_i – , а при t > t_i – = const.

Щоб усунути невизначеність значень при t = t_i — під час проведення розрахунків рівняння (5.6) потрібно використовувати у вигляді:

,

де δ — деяка досить незначна величина, наприклад, 10^–9 с.

Тоді для n-дисперсної системи масу осаду з часом слід описувати рівнянням:

. (5.7)

Рівняння (5.7) має описувати будь-яку седиментаційну криву, незалежно від закону розподілу частинок полідисперсної системи за радіусами. Однак рівняння (5.7) містить невідомі величини , які потрібно визначити за експериментальними даними їх кількість визначається кількістю фракцій у полідисперсній системі (n).

Розрахунок фракційного складу (величин ) базується на визначенні таких величин , для яких теоретична седиментаційна крива за рівнянням (5.7) та експериментальна якнайкраще збігаються. Зазвичай для розв’язання таких задач використовують метод найменших квадратів:

, (5.8)

де — маса осаду, розрахована за рівнянням (5.7); — експериментальні значення маси осаду; k — кількість експеримен-тальних вимірювань (k ≥ n).

Для знаходження мінімуму функції мети існують різні методи. Досить зручним для практичних розрахунків величин рівняння (5.8) є метод Ньютона, який вбудований у MS EXCEL у програмі ПОИСК РЕШЕНИЯ.

Фактично програма ПОИСК РЕШЕНИЯ, використовуючи метод Ньютона, підбирає величини за умовою мінімуму функції мети.

Для використання можливостей MS EXCEL і розрахунків функ-ції мети , було розроблено програму Function SED25 мовою Visual Basic.

Function SED25 (N, NT, a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13, a14, a15, a16, a17, a18, a19, a20, a21, a22, a23, a24, a25)

Dim x As Double, i As Integer

Dim j As Integer

Dim v As Double, s As Double, z As Double, y As Double

Dim m As Double, mm As Double, mmm As Double, f As Double

x = 0

v = 0

s = 0

'N — кількість фракцій

'NТ — кількість експериментальних значень маси осаду

For j = 1 To NT

y = Cells(j, 2).Value

'y — час t

s = 0

For i = 1 To N

x = Cells(i, 1).Value

'х — час t_i

mm = Cells(i, 3).Value

'mm – маса

a = 0.000000001

s1 = (((x - y) ^ 2) ^ 0.5) + a

s2 = (x – y + a)

m = ((mm / x) * y / 2) * (1# + s2 / s1) + (mm / 2#) * (1# – s2 / s1)

s = s + m

Next i

mmm = Cells(j, 4).Value

'mmm- маса Q_екс

f = (s - mmm) ^ 2

'f — це (Q-Qпрак)^ 2

v = v + f

Next j

SED25 = v

End Function

Function PIDBIRINTEGRAL (NT, a1, a2, a3, a4)

Dim x As Double, i As Integer

Dim j As Integer

Dim v As Double, s As Double, z As Double, y As Double

Dim m As Double, mm As Double, mmm As Double, f As Double

'Програма вибору теоретичних інтегральних функцій розподілу

x = 0

s = 0

For i = 1 To NT

y = Cells(i, 22).Value

'y — експериментальна інтегральна функція розподілу

z = Cells(i, 16).Value

'z = 1 — ЛОГНОРМРАСП(x, a1, a2) або інша теоретична

' інтегральна функція розподілу!!!

' Обов’язково перевіряти відповідність номерів стовпчиків

'у яких знаходяться значення z та y

s1 = (z – y) ^ 2

s = s + s1

Next i

PIDBIRINTEGRAL = s

End Function

Результати розрахунків за експериментальними даними дають змогу визначити фракційний склад зразків (величин _max).

За розрахованими величинами можна побудувати інтегральну функцію розподілу частинок полідисперсної системи за радіусами, а далі, аналізуючи інтегральну функцію, визначити закон розподілу частинок за розмірами (рівномірний, нормальний, логарифмічно-нормальний, степеневий і т. п.).

За даними седиментаційного аналізу можна також визначити питому поверхню (поверхню одиниці об’єму) порошку. Питома по-верхня порошку s_υ дорівнює сумі питомих поверхонь усіх фракцій:

де s_i — питома поверхня відповідної фракції; — загальна маса фракцій.

Питома поверхня кожної фракції дорівнює відношенню по-верхні всіх п частинок даної фракції до їх об’єму і для сферичних частинок дорівнює:

де r_і — середній радіус частинок даної фракції.

Тоді питома поверхня порошку: .

Щоб знайти питому поверхню s_m одиниці маси порошку, треба поверхню одиниці об’єму розділити на питому вагу  порошку:

см²/г.

Наявність рівняння, що описує інтегральну криву розподілу частинок полідисперсної системи за радіусами, надає можливість визначити питому поверхню порошку з потрібною точністю:

де r₁ та r₁+nΔr — значення мінімального та максимального радіусів; n — кількість фракцій; Δr — крок зміни радіусу.

Розглянемо на прикладі застосування методу Ньютона для обробки даних седиментаційного аналізу, за допомогою якого можна визначати фракційний склад полідисперсної суспензії незалежно від закону розподілу частинок полідисперсної системи за радіусами.

При проведенні седиментаційного аналізу суспензії глини у воді були отримані усереднені дані про залежність маси (Q) частинок суспензій, що осіли, від часу осідання t, які наведені в таблиці.

t, с	Q, мг	t, с	Q, мг
30	8,1	1320	103,6
60	16,3	1560	109,1
120	32,6	1800	113,7

Закінчення

t, с	Q, мг	t, с	Q, мг
180	48,3	2100	118,4
240	60,9	2400	122,0
300	69,1	2760	125,2
360	74,1	3300	128,4
420	77,3	3900	130,4
480	79,7	4800	131,8
600	83,7	6000	132,6
720	87,3	8400	132,9
840	90,7	10800	133,0
1080	97,4

Умови досліду: H = 0,08 м; _{середовища} = 110^–3 Пас; _глини = = 3,410³ кг/м³; ₀ = 1,0010³ кг/м³.

Потрібно:

• визначити фракційний склад суспензії;

• побудувати інтегральну функцію розподілу частинок полі-дисперсної системи за радіусами;

• визначити закон розподілу частинок дисперсної фази за розмірами;

• визначити питому поверхню (поверхню одиниці об’єму) порошку.

При проведенні розрахунків урахувати, що кількість фракцій дорівнює кількості вимірювань.

Відповідно до умов, які містяться в програмі Function SED25 у MS EXCEL, стовпчики A, B, D заповнюємо значеннями t, t_i, m_eкс. Далі обчислюємо константу K (у комірці I 3):

= (9110^–3/2(3,4 – 1,00)10³9,81)^0,5 =0,43710^–3с^0,5 м^0,5.

У стовпчику К розрахуємо радіуси частинок фракцій:

У комірці H 11 запишемо розрахунок функції мети:

SED25(25;25;C1;C2;C3;C4;C5;C6;C7;C8;C9;C10;C11;C12;C13; C14;C15;C16;C17;C18;C19;C20;C21;C22;C23;C24;C25).

Стовпчик С зарезервуємо для розрахунків фракційного складу (величин _max), а комірку С29 – для розрахунків суми величин _max (рис. 5.35).

Рис. 5.35. Використання ЕХСЕL для обробки даних седиментаційного аналізу

Після цього заходимо у програму «Поиск решения» і встановлюємо:

«Установить целевую ячейку $H$11, равной минимальному значению, изменяя ячейки $C$1:$C$25, ограничение $C$29 < = 145» (рис. 5.36).

Заходимо в опцію програми «Поиск решения» «параметры» і встановлюємо параметри пошуку рішення: «максимальное время 1000 с, предельное число итераций 1000, относительная погрешность 0,0000001, допустимое отклонение 0,0000001, сходимость 0,00000000001, неотрицательные значения», натискаємо «ОК», а потім «Выполнить» (рис. 5.37).

Рис. 5.36. Відкривання вікна «Поиск решения»

Рис. 5.37. Відкривання вікна «Параметры поиска решения»

У результаті пошуку рішення у стовпчику С розраховано фракційний склад суспензії (рис. 5.38).

Рис. 5.38. Вікно результатів пошуку розв’язку

Фракційний склад суспензії дає можливість визначити значення інтегральної функції розподілу в стовпчику К і побудувати відпо-відну залежність (рис. 5.39).

Рис. 5.39. Аркуш MS EXCEL із результатами пошуку розв’язку і залежність інтегральної функції розподілу від радіусів частинок

Зовнішній вигляд інтегральної функції розподілу свідчить, що графік диференціальної функції розподілу частинок суспензії за радіусами повинен мати два максимуми, тобто розподіл бімодальний. Двомодальну інтегральну функцію розподілу частинок часто описують сумою двох рівнянь логарифмічно-нормального або нормального закону.

Для логарифмічно-нормального закону:



Для нормального закону:

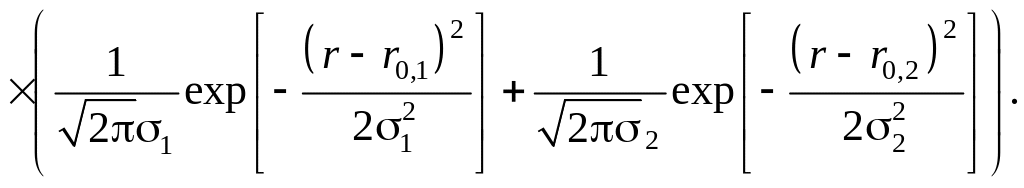
Використання методу найменших квадратів дає змогу вибрати найкращу функцію для опису інтегральної кривої розподілу і базується на знаходженні мінімуму функції мети:

Для визначення величин r_0,1, r_0,2, ₁, ₂ для логарифмічно-нормального закону розподілу у стовпчику Р набираємо вираз для розрахунку інтегральної функції розподілу частинок (F(r)_теор):

=1-0,5*(ЛОГНОРМРАСП(H1;$F$20;$F$21) + + ЛОГНОРМРАСП(H1;$F$22;$F$23)).

У стовпчику К за величинами мас окремих фракцій, які були розраховані у стовпчику С, розраховуємо інтегральну функцію розподілу частинок (F(r)_екс).

Функцію мети PIDBIRINTEGRAL(25;F20;F21;F22;F23) набираємо в комірці G14. Після цього заходимо в програму «Поиск решения» і встановлюємо потрібні опції (рис. 5.40).

Рис. 5.40. Відкриття вікна «Параметры поиска решения»

У результаті пошуку рішення в комірках F20; F21; F22; F23 розраховуються величини r_0,1, r_0,2, ₁, ₂ (рис. 5.41).

Рис. 5.41. Аркуш MS EXCEL із результатами пошуку розв’язку

Для визначення величин r_0,1, r_0,2, ₁, ₂ для нормального закону розподілу у стовпчику Р набираємо вираз для розрахунку інтег-ральної функції розподілу частинок (F(r)_теор):

=1–0,5*НОРМРАСП (I1; $F$20; $F$21; ИСТИНА) + + НОРМРАСП(I1; $F$22; $F$23; ИСТИНА).

Порівняння значень мінімумів функції мети для нормального і логарифмічно-нормального закону розподілу засвідчує, що інтегральну функцію розподілу частинок краще описувати сумою двох рівнянь логарифмічно-нормального закону.

Далі обчислимо питому поверхню порошку:

3,73  10⁷ м^–1.

Завдання для розрахункової роботи

При проведенні седиментаційного аналізу суспензії тальку у воді було отримано дані, наведені в таблиці в шести варіантах.

Умови досліду: H = 0,08 м; _{середовища} = 110^–3 Пас; _глини = = 3,410³ кг/м³; _о = 1,0010³ кг/м³.

Варіант	1	2	3	4	5	6
t, с	Q, мг	Q, мг	Q,мг	Q, мг	Q, мг	Q, мг
30	19,2	10,1	10,8	9,0	4,5	11,6
60	38,4	20,4	21,7	18,1	9	23,1
120	75,4	40,8	43,3	36,2	18	45,1
180	98,3	60,4	64,2	54,2	26,8	63,4
240	110,2	76,1	80,9	71,6	35,2	77,6
300	116,8	86,4	91,9	86,4	43,1	88,5
360	120,6	92,6	98,5	97,7	50,3	96,8
420	123,1	96,6	102,8	105,9	56,9	103,2
480	124,7	99,6	106,0	111,7	62,9	108,1
600	127,0	104,6	111,3	119,9	73,7	115,7
720	128,4	109,1	116,1	124,3	82,4	120,5
840	129,2	113,3	120,6	126,8	89,6	123,6
1080	130,2	121,7	129,5	129,7	101,2	127,9
1320	130,8	129,5	137,8	131,0	109,2	130
1560	131,2	136,4	145,1	131,7	114,8	131,1
1800	131,4	142,1	151,2	132,0	118,8	131,7
2100	131,6	148,0	157,4	132,3	122,4	132,2
2400	131,8	152,5	162,2	132,5	124,8	132,5
2760	131,9	156,5	166,5	132,6	126,9	132,7
3300	132,0	160,5	170,7	132,7	129,0	132,8
3900	132,1	163	173,4	132,8	130,3	132,9
4800	132,2	164,8	175,3	132,8	131,4	133
6000	132,3	165,8	176,4	132,9	132,1	133
8400	132,4	166,1	176,7	132,9	132,6	133
10800	132,4	166,2	176,9	132,9	132,7	133

Потрібно:

• визначити фракційний склад суспензії;

• побудувати інтегральну функцію розподілу частинок полі-дисперсної системи за радіусами;

• залежно від вигляду графіка визначити закон розподілу частинок дисперсної фази за розмірами (одно- чи двомодальний);

• якщо розподіл одномодальний, порівняти значення мінімумів функції мети , вважаючи, що закон розподілу частинок описується рівнянням логарифмічно-нормального або нормального закону розподілу;

• для двомодальної функції розподілу частинок порівняти значення мінімумів функції мети, вважаючи, що закон розподілу частинок описується сумою двох рівнянь логарифмічно-нормального або нормального законів;

• визначити питому поверхню (поверхню одиниці об’єму) порошку.

При проведенні розрахунків взяти до уваги, що кількість фракцій дорівнює кількості експериментальних значень вимірювань маси осаду.

Розрахункова робота 15