Розрахункова робота 1-2

Завдання 1. С татистична обробка експериментальних даних при значних вибірках

Мета роботи: навчитися виконувати статистичну обробку при значних вибірках значень експериментальних даних.

Теоретичні відомості

Завданням більшості фізико-хімічних експериментів є кількісне вивчення яких-небудь Метою статистичної обробки результатів повторних вимірювань є подання результату у формі

x = ± ∆х,

де — середнє арифметичне значення; ∆х — надійний інтервал прямого вимірювання.

Статистична обробка результатів повторних вимірювань складається з двох етапів: перший –– виявлення грубих похибок; другий –– розрахунок надійного інтервалу ∆х.

Для виявлення грубих похибок найчастіше використовують розглянуті далі чотири методи.

1. Найпростішим методом знаходження грубих похибок є таке правило: відхилення випадкових величин від середнього значення (d = x_i – ) за модулем не має перевищувати 3S (3S-критерій).

Згідно з цим правилом похибка вважається грубою, якщо

> 3S,

де , а — найменше або найбільше з вимірюваних значень.

2. Q-критерій. Якщо кількість повторних вимірювань незначна (n < 10), обчислюють відношення

Q = ,

де x₁ –– підозріле значення вимірюваної величини; х₂ –– найближче значення до величини х₁; R –– інтервал варіювання, R = x_max – x_min — різниця між найбільшим і найменшим значеннями.

Обчислене значення Q порівнюють із табличними значеннями Q_табл (p, n) (табл. Д.1.3). Похибка вважається грубою за умови, що

Q > Q_табл (p, n).

3. β-критерій. Нехай маємо вибірку x₁, x₂, …, x_n значень нор-мально розподіленої випадкової величини x. Позначимо через х_max (x_min) найбільший (найменший) результат вимірювань. Величини

(3.1)

та

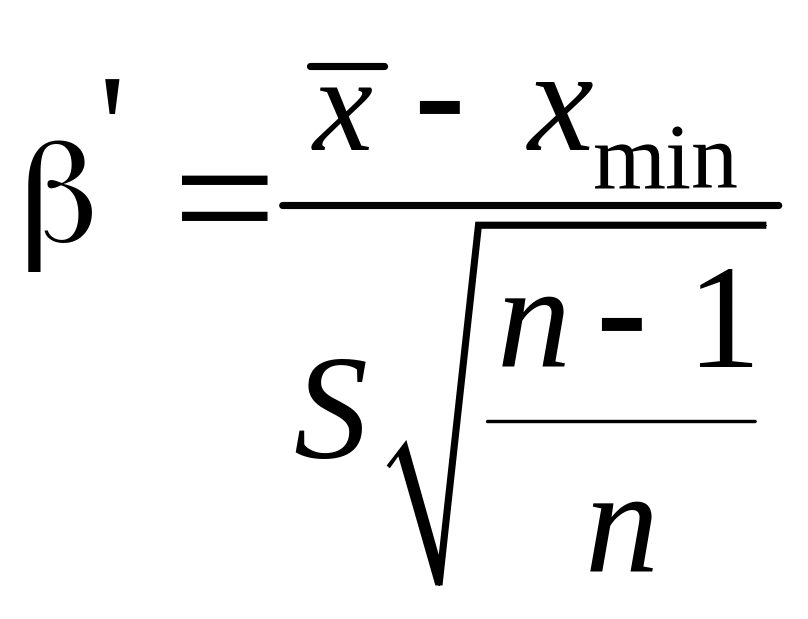(3.2)

мають спеціальний розподіл, який залежить тільки від кількості степенів вільності f = n – 2. У табл. Д.1.4 наведено максимальні значення β (β′) для рівня значущості α = 1 – р = 0,1; 0,05 та 0,01 для кількості степенів вільності від 1 до 22. Значення х_max (x_min) виключається з вибірки як результат грубого вимірювання (на рівні значущості якщо визначене за формулою (3.1) або (3.2) значення β або β′ виявиться більшим від табличного.

Якщо сумнів викликають два або три елементи вибірки, діють у такий спосіб. Для всіх сумнівних елементів обчислюють β (β′) і починають дослідження з елемента, що має найменше значення β (β′). Інші сумнівні елементи з вибірки виключаються. Для цієї зменшеної вибірки обчислюють , S та нове значення β (β′) для досліджуваного елемента. Якщо досліджуваний елемент не є результатом грубого вимірювання, його приєднують до вибірки та починають досліджувати наступний за абсолютною величиною β (β′) елемент вибірки, при цьому знову обчислюючи нові значення та S, і т. д.

4. Критерій Романівського. Цей критерій використовують для малих вибірок. Із цією метою для заданого рівня значущості 1 – р залежно від кількості степенів вільності f = n – 2 обчислюють максимально припустиме, тобто граничне, значення абсолютної по-хибки окремого вимірювання:

∆х_гран= Sq,

де стандартне відхилення S обчислюється за значенням х з виключенням підозрілих значень можливих промахів:

S = ;

значення q для заданого рівня значущості 1 – р залежно від n наведено в табл. Д.1.5.

Якщо > ∆х_гран, то похибка вважається грубою і підозріле значення не враховується.

Після виявлення грубих похибок їх відкидають і для решти значень провадять дальшу статистичну обробку –– оцінку надійного інтервалу вимірювання ∆х. З цією метою задаються певним значенням надійності p і розраховують ∆х за формулою

∆x = S_x,

де – коефіцієнт Стьюдента, значення якого знаходять за табл. Д.1.2 залежно від вибраної надійної ймовірності p і кількості степенів вільності f (f = n –1).

Надійний інтервал ∆х визначає точність вимірювань і тому може виражатись як абсолютною величиною, так і відносною похибкою, вираженою у відсотках:

100 %.

Отже, можна скласти поетапну схему обробки результатів пов-торних вимірювань.

1. Розрахунок середнього значення вимірюваної величини та від­хилень значень вимірюваних величин від середнього значення.

2. Розрахунок дисперсії, стандартного відхилення і стандартного відхилення середнього значення.

3. Визначення і виключення грубих похибок за розглянутими критеріями.

4. Після виключення грубих похибок повторюють попередні розрахунки. Якщо немає грубих похибок, розраховують надійний інтервал ∆х.

Після статистичної обробки остаточний запис результатів повторних вимірювань фізичних величин матиме вигляд:

x = + ∆x.

Приклад. Студенти, які виконували вимірювання за допомогою рН-метра з використанням скляного електрода, дістали для одного і того самого розчину кислоти такі значення рН:

рН	5,1	5,2	5,3	5,4	5,5	5,6	5,7	5,8	6,0
N	1	16	28	36	28	14	2	1	1

де N — кількість отриманих значень рН.

Потрібно провести статистичну обробку даних і розрахувати рН розчину кислоти.

Щоб виконати це завдання, потрібно діяти за такою схемою:

1) визначити середнє значення рН розчину кислоти;

2) розрахувати відхилення значень окремих вимірювань рН;

3) розрахувати стандартне відхилення;

4) визначити і виключити грубі похибки за 3S-критерієм;

5) після виключення грубих похибок знову розрахувати стан-дартне відхилення;

6) розрахувати точність прямого вимірювання;

Розрахунки для статистичної обробки даних повторних вимірювань зручно проводити за допомогою MS EXCEL (рис. 3.1).

Рис. 3.1. Приклад обробки експериментальних даних за допомогою MS EXCEL

Для цього спочатку стовпець А заповнюємо вихідними значеннями рН, а стовпець В –– значеннями N. У комірці В10 розраховуємо загальну кількість вимірювань (суму значень N); у комірці С10 — загальну суму значень рН; у комірці С11 –– середнє арифметичне, що згідно з рівнянням (2.3) визначається так:

= = 687/127 = 5,407.

Далі виконуємо розрахунки з первинної обробки для виявлення грубих похибок.

Розраховуємо у стовпці D окремі відхилення від середнього d_i.

Далі виконуємо розрахунок:

–– дисперсії S² (комірка C12):

S² = 2,5436/126 = 0,0202;

–– стандартного відхилення S (комірка C13):

S = (0,0202)^0,5 = 0,1421.

Для визначення грубих похибок використовуємо критерій стандартного відхилення середнього (комірка C14):

> 3S = 0,4262.

Порівнюючи знайдене значення 0,4262 зі значеннями у стовпці окремих відхилень d, виявляємо один промах — значення рН = 6.

Відкидаємо його і проводимо вторинну обробку (рис. 3.2).

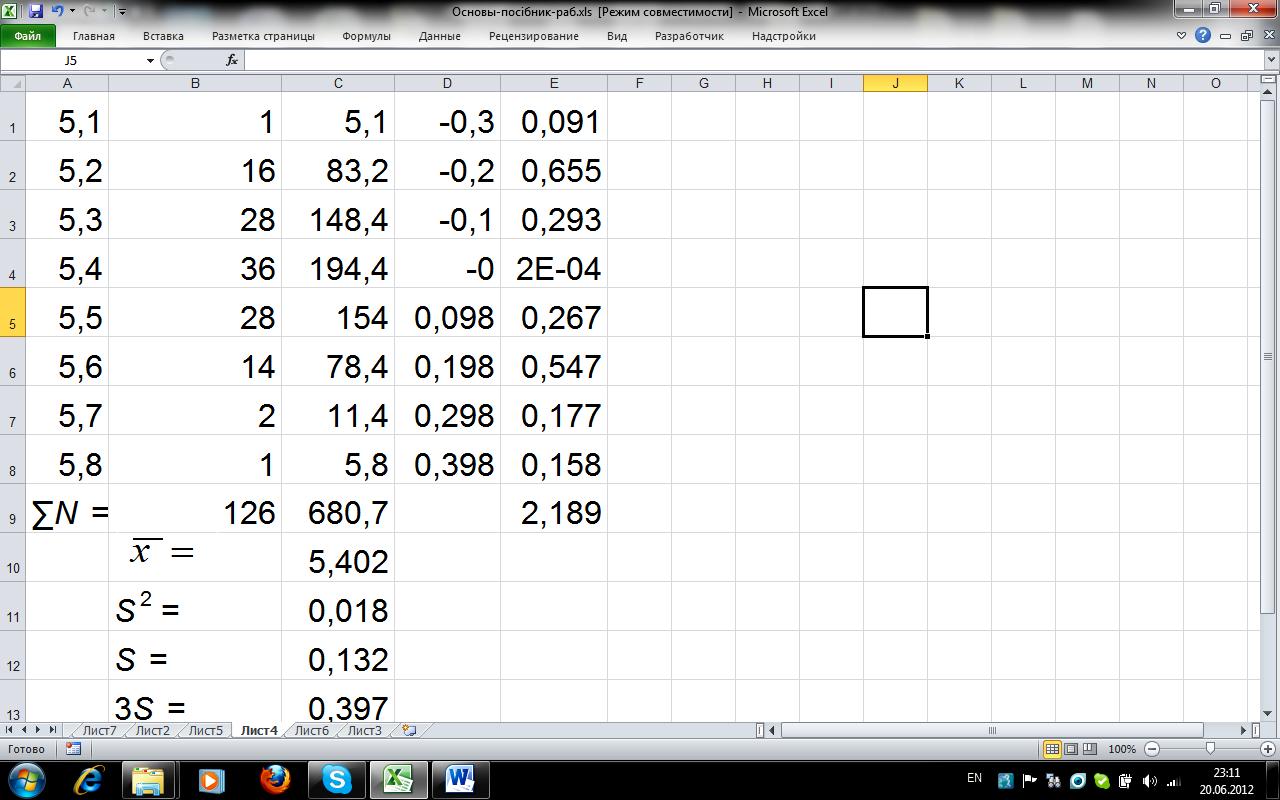
Рис. 3.2. Оброблення експериментальних даних після виключення першої грубої похибки

Знову для визначення грубих похибок використовуємо критерій стандартного відхилення середнього:

> 3S = 0,397.

Порівнюючи знайдене значення 0,397 зі значеннями у стовпці відхилень d, виявляємо один промах –– значення рН = 5,8.

Відкидаємо його і проводимо подальшу обробку (рис. 3.3).

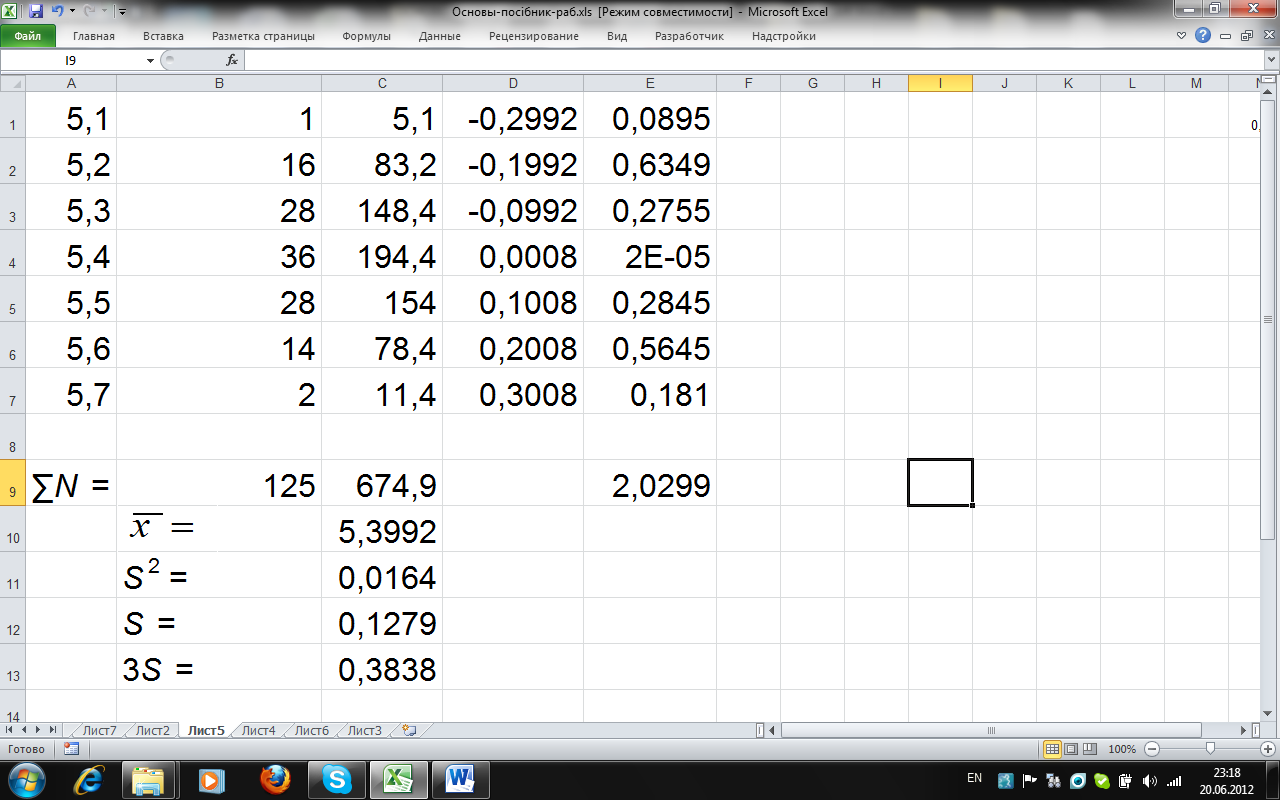
Рис. 3.3. Обробка експериментальних даних після виключення другої грубої похибки

Порівнюючи знайдене значення 0,3838 зі значенням у стовпці окремих відхилень d, не виявляємо промахів.

Задаємось надійною ймовірністю p = 95 %, знаходимо з табл. Д.1.2 значення коефіцієнта Стьюдента для f = 125 – 1 = 124: t_pf = 1,98 i згідно з рівнянням (3.6) знаходимо точність прямого вимірювання:

∆х = 1,98·0,1279 = 0,25.

Отже, за результатами проведеної статистичної обробки (округлюючи остаточний результат до необхідної точності) маємо:

рН = 5,40 ± 0,25.

З огляду на те, що кількість вимірювань (вибірка) достатньо значна, можна проводити розрахунки, використовуючи функцію Лапласа. Знаходимо з табл. Д.1.1 при p = 95 % значення U =1,95.

Тоді ∆х = 1,95 · 0,1279 = 0,25, чим підтверджується збіг результатів розрахунків при значній кількості вимірювань у разі використання функції Лапласа або коефіцієнта Стьюдента.

Для незначних вибірок (кількість вимірювань менша від 10) значення грубої похибки є визначальним при розрахунку дисперсії

S² = ,

а тому використовувати 3S-критерій немає сенсу. Справді,

,

де = .

Тоді, припустивши наявність грубої похибки: (ω –– деяке додатне число), дістанемо

.

Оскільки права частина цієї рівності завжди додатна, то з цього випливає, що значення також додатне. Це можливо принаймні при n > 10 (при ω = 0).

Тому для малих вибірок використовують критерій Романівського, Q- чи β-критерій.

Розглянемо приклад статистичної обробки експериментальних даних у разі незначної вибірки.

Приклад. Провести статистичну обробку наведених у таблиці даних повторних вимірювань рН:

рH

4,28

4,26

4,30

4,29

4,30

4,30

4,20

4,00

Визначаємо середнє значення вимірюваної величини:

стандартне відхилення S = 0,1032; критерій Q = 0,667, критерій β’= 2,50.

Для розрахунку критерію Романівського відкидаємо підозрілу точку рН = 4 і визначаємо значення S = 0,0364. Далі обчислюємо припустиму абсолютну похибку окремого вимірювання:

∆рН _гран = Sq = 0,0364∙2,62 = 0,0955.

Із табл. Д.1.3 та Д.1.4 для надійної ймовірності р = 0,95 беремо значення критеріїв Q = 0,48 та β = 2,172. Порівнюємо обчислені значення Q = 0,667 та β’ = 2,50 з табличними Q = 0,48 та β = 2,172.

Обидва обчислені значення більші за табличні. За критерієм Романівського = 0,276 > ∆рН _гран.

Висновок: за всіма критеріями значення рН = 4 знайдено з грубою похибкою. Відкидаємо це значення та повторюємо розрахунки.

Визначаємо середнє значення вимірюваної величини:

; стандартне відхилення S = 0,0364; критерій Q = 1,0; критерій β = 2,24. Відкидаємо підозрілу точку рН = 4,2 і знаходимо значення S = 0,016. Далі обчислюємо припустиму абсолютну похибку окремого вимірювання: ∆рН _гран = Sq = 0,016∙2,78 = 0,0445.

За критерієм Романівського = 0,088 > ∆рН _гран.

Із таблиць Д.1.3 і Д.1.4 (додаток 1 ) для надійної ймовірності р = 0,95 беремо значення критеріїв Q = 0,51 та β= 2,093.

Висновок: за критеріями Q, β’ та Романівського значення рН = 4,2 знайдено з грубою похибкою. Відкидаємо це значення та повторюємо розрахунки.

Визначаємо середнє значення вимірюваної величини: рН = 4,288, стандартне відхилення S = 0,016; критерій Q = 0,5; критерій β = 0,57.

Відкидаємо підозрілу точку рН = 4,26 і визначаємо значення S = 0,0089. Далі обчислюємо припустиму абсолютну похибку окремого вимірювання: ∆рН _гран= Sq = 0,0089∙3,04 = 0,0272. За критерієм Романівського

= 0,034 >∆рН _гран.

Із табл. Д.1.3 і Д.1.4 для надійної ймовірності р = 0,95 беремо значення критеріїв Q = 0,56 і β = 1,996.

Висновок: за критеріями Q, β’ значення рН = 4,26 не належить до обчислених із грубою похибкою, а за критерієм Романівського є грубою похибкою.

Відкидаємо це значення та повторюємо розрахунки і отримаємо, що за всіма критеріями значення рН = 4,28 не належить до обчислених із грубою похибкою.

Узявши р = 0,95, знайдемо за табл. Д.1.2 значення коефіцієнта Стьюдента для f = 6 – 1 = 5: = 2,57 і згідно з рівнянням (3.6) знаходимо точність прямого вимірювання:

∆рН = 2,57· 0,0089 = 0,023.

Таким чином, унаслідок виконаної статистичної обробки (ок-ругливши остаточний результат до необхідної точності) дістанемо:

рН = 4,288 ± 0,023.

Завдання для розрахункової роботи

Провести статистичну обробку наведених у таблиці даних повторних вимірювань рН, скориставшись поетапною схемою обробки результатів вимірювань.

1. Визначити середнє значення вимірюваної величини рН.

2. Розрахувати відхилення значень окремих вимірювань величини рН від середнього.

3.Розрахувати дисперсію, стандартне відхилення та стандартне відхилення середнього значення.

4. Визначити та виключити грубі похибки за 3S-критерієм.

5. Після виключення грубих похибок знову розрахувати значення дисперсії, стандартного відхилення та стандартного відхилення середнього значення.

6. Розрахувати точність прямого вимірювання і остаточний запис результатів статистичної обробки подати у вигляді:

7. Після виключення грубих похибок розрахувати величини, які необхідні для побудови:

1) графіка розподілу ймовірностей значень рН (гістограма);

2) графіка інтегральної функції розподілу рН;

Далі побудувати вказані графіки.

8. Побудувати залежність функції щільності ймовірності від значень рН за законом нормального розподілу.

9. Скориставшись вбудованою в MS EXCEL функцією НОРМРАСП (рН_i ; ; S; «інтегральна»), обчислити значення інтегральної функції розподілу значень рН (для всіх значень рН) та значення функції щільності розподілу значень рН. За знайденими розрахунковими (теоретичними) даними побудувати графіки залежності інтегральної функції розподілу рН та функції щільності ймовірності від значень рН.

Експериментальні значення рН та відповідна кількість N їх повторювань для 30 різних варіантів (В) завдання наведено в таблиці.

В –– 1	рH	4	4,1	4,2	4,3	4,4	4,5	4,6	4,8	5
	N	1	16	27	38	26	14	2	1	1
В –– 2	рH	3,5	3,6	3,7	3,8	3,9	4	4,1	4,2	4,3
	N	1	12	22	32	22	11	2	1	1
В –– 3	рH	4,7	4,8	4,9	5	5,1	5,2	5,3	5,4	5,5
	N	1	11	21	32	22	12	3	1	1
В –– 4	рH	5,4	5,5	5,6	5,7	5,8	5,9	6	6,1	6,2
	N	1	9	19	33	20	10	2	1	1
В –– 5	рH	5,8	5,9	6	6,1	6,2	6,3	6,4	6,5	6,6
	N	1	11	23	36	24	12	3	1	1
В –– 6	рH	6	6,1	6,2	6,3	6,4	6,5	6,6	6,7	6,8
	N	1	12	24	36	23	13	4	1	1
В –– 7	рH	6,2	6,3	6,4	6,5	6,6	6,7	6,8	6,9	7
	N	1	15	23	36	22	14	2	1	1
В –– 8	рH	4,3	4,4	4,5	4,6	4,7	4,8	4,9	5	5,1
	N	1	10	18	28	19	11	2	1	1
В –– 9	рH	5,5	5,6	5,7	5,8	5,9	6	6,1	6,2	6,3
	N	1	10	21	30	20	12	3	1	1
В –– 10	рH	6,2	6,3	6,4	6,5	6,6	6,7	6,8	6,9	7
	N	1	11	24	38	25	12	3	1	1
В –– 11	рH	6,4	6,5	6,6	6,7	6,8	6,9	7	7,1	7,2
	N	1	13	21	36	22	14	3	1	1
В –– 12	рH	7	7,1	7,2	7,3	7,4	7,5	7,6	7,7	7,8
	N	1	11	17	28	18	12	2	1	1
В –– 13	рH	6,6	6,7	6,8	6,9	7	7,1	7,2	7,3	7,4
	N	1	9	18	30	19	10	3	1	1
В –– 14	рH	6,4	6,5	6,6	6,7	6,8	6,9	7	7,1	7,2
	N	1	1	9	18	30	19	10	3	1
В –– 15	рH	6,4	6,5	6,6	6,7	6,8	6,9	7	7,1	7,2
	N	1	9	18	30	19	10	3	1	1
В –– 16	рH	6,4	6,5	6,6	6,7	6,8	6,9	7	7,1	7,2
	N	1	1	9	18	38	19	8	2	1
В –– 17	рH	5,2	5,3	5,4	5,5	5,6	5,7	5,8	5,9	6
	N	1	1	9	24	41	23	10	2	1
В –– 18	рH	4,3	4,4	4,5	4,6	4,7	4,8	4,9	5	5,1
	N	1	1	9	28	41	27	10	3	1
В –– 19	рH	5,5	5,6	5,7	5,8	5,9	6	6,1	6,2	6,3
	N	1	2	11	26	41	25	10	2	1
В –– 20	рH	4,4	4,5	4,6	4,7	4,8	4,9	5	5,1	5,2
	N	0	1	9	24	38	23	10	1	1
В –– 21	рH	5,6	5,7	5,8	5,9	6	6,1	6,2	6,3	6,4
	N	0	1	9	24	41	23	10	2	0
В –– 22	рH	9,4	9,5	9,6	9,7	9,8	9,9	10	10,1	10,2
	N	1	1	9	24	41	23	10	2	1
В –– 23	рH	10,1	10,2	10,3	10,4	10,5	10,6	10,7	10,8	10,9
	N	1	3	9	22	38	23	10	2	1
В –– 24	рH	9	9,1	9,2	9,3	9,4	9,5	9,6	9,7	9,8
	N	1	1	9	19	33	20	8	1	1
В –– 25	рH	8,4	8,5	8,6	8,7	8,8	8,9	9	9,1	9,2
	N	1	1	9	24	35	23	8	2	1
В –– 26	рH	7,9	8	8,1	8,2	8,3	8,4	8,5	8,6	8,7
	N	1	1	6	18	35	17	8	2	1
В –– 27	рH	7,5	7,6	7,7	7,8	7,9	8	8,1	8,2	8,3
	N	1	2	9	28	41	27	10	2	1
В –– 28	рH	8,8	8,9	9	9,1	9,2	9,3	9,4	9,5	9,6
	N	1	2	9	22	44	23	8	2	1
В –– 29	рH	7,7	7,8	7,9	8	8,1	8,2	8,3	8,4	8,5
	N	1	1	7	18	34	19	8	2	1
В –– 30	рH	6,5	6,6	6,7	6,8	6,9	7	7,1	7,2	7,3
	N	1	1	18	27	44	28	17	2	1