Володіння комп'ютером

Групи, в яких	Виявлено учнів (п)		Всього (п)
проводили тестування	Володіють (> 70 %)	Не володіють (< 70 %)
Група 1	30	22	52
Група 2	25	23	48
Всього (п)	55	45	100

Групування у найпростішому випадку виконується на основі якої-небудь однієї ознаки педагогічного явища чи процесу. Складність цієї дії полягає в тому, що ознака змінюється в широких чи вузьких межах.

Основне призначення таблиць полягає 8 тому, щоб зробити доступним для огляду статистичний матеріал і полегшити можливості порівняння та зіставлення чисел. Проте в прЬцесі ознайомлення з числами досить важко усвідомити різні аспекти поданих даних і утримати в пам'яті їхні співвідношення. Допомагає в цьому використання інших засобів наочного уявлення - малюнків, що дають змогу сприйняти одночасно більше інформації, ніж дають ряди цифр, і виробити певну точку зору на значення наведених результатів.

Статистичну обробку дослідних даних, навіть у вибірках невеликого обсягу, досить важко виконати технічно без попереднього їх групування в класи. Це групування може бути природним і штучним залежно від типу мінливості ознаки, але щодо останнього необхідно дотримуватися певних правил, які дають змогу уникнути зміщення показників вибірки.

Кожне поодиноке значення (хі, х₂, х₃, ... х„), яке здатна набувати певна ознака (х), називається варіантою. Кількість досліджуваних, які володіють даним значенням ознаки, становлять частоту (f) появи даної варіанти у вибірці. Спільний ряд варіант і відповідних їм частот (х, f), утворюють варіаційний ряд, який потребує подальшої обробки.

При альтернативній мінливості групування даних не викликає утруднень, оскільки кількість природних класів варіювання ознаки збігається з кількістю варіант (таблиця 8)

Попередня обробка такого роду полягає в обчисленні відсотку появи кожного значення ознаки у вибірці.

При дискретному варіюванні ознаки групування даних, звісно, також є природним, хоча кількість класів збільшується. Такі чотирипільні таблиці мають не тільки ілюстративне значення, але й є зручною формою групування первинних даних під час обчислення показників кореляційної залежності між якісними (альтернативними) ознаками.

Таблиця 8

Розподіл правильних і неправильних відповідей у вибірці (альтернативний тип мінливості ознаки)

		F	% від п
Правильні	X,	91	60,7
Помилкові	Х2	59	39,3
	N	150	100

Більш складними е багатопільні таблиці, які застосовують у процесі групування вихідних даних для виявлення причинно-наслідкових відношень між об'єктами, які варіюють (таблиця 9).

При цьому одні ознаки розглядають як фактори, що впливають на інші ознаки, які називають результативними.

Для педагогічних досліджень особливо цікавим є групування вихідних даних у статистичні ряди - ряди числових значень ознаки, розміщених у певній послідовності. В залежності від того, в якому плані (статики чи динаміки) і за якими ознаками (якісними чи кількісними) розглядають явища або процеси, статистичні ряди поділяють на атрибутивні, варіаційні (ряди динамічні), ранжовані та ін.

Прикладом атрибутивного ряду може бути розподіл 50 учнів за ознаками позитивних емоцій, нейтрального ефекту або негативних емоцій від вивчення художнього твору (таблиця 10).

Іншим прикладом атрибутивного ряду можуть бути дані, за якими можна простежити зростання кількості релевантних (доречних) запитань, відповідей учнів під час вивчення певного навчального предмету протягом півріччя залежно від стилю роботи вчителя.

Зрізові вимірювання	І	II	III	IV
Сумарна тривалість релевантних запитань і відповідей (хв)	5	7	10	ІЗ

У тих випадках, коли зміни ознаки розглядаються залежно від фактору часу, тоді маємо справу з рядами динаміки, які ще називаються часовими. Отже, характерна особливість рядів динаміки та, що в ролі незалежної змінної тут завжди виступає фактор часу. Така залежність має однобічний характер, оскільки фактор часу не залежить від зміни ознаки. Прикладом такого ряду може бути кількість відмінних оцінок (у %) від загальної кількості оцінок за кожен рік навчання.

Варіаційним рядом називається ряд чисел, у якому одиниці досліджуваної сукупності розподіляються за ранжованими значеннями ознаки, яка змінюється (варіює). Наприклад, після завершення вивчення курсу фізики учнями чотирьох десятих класів в умовах експериментальної технології навчання випадковим способом, тобто навмання, було відібрано 25 учнів. Підраховувалася кількість самостійних завдань, виконаних цими учнями за навчальний рік. Результат виявився таким: 6, 9, 5, 10, 7, 9, 8, 10, 9, 10, 8, 11, 9, 12. 9, 10, 8, 10, 11, 9, 10, 9, 8, 7, 11. Розташуємо ці дані у порядку зростання числових значень ознаки, тобто ранжуємо таким чином, щоб підрахувати, скільки разів кожна варіанта (хі) зустрічається у даній сукупності. Оскільки ознака варіює в межах від 5 до 12 одиниць, вибірка розподіляється так:

Значення ознаки (хі)	5	6	7	8	9	10	11	12
Кількість варіант (рі)	1	1	2	4	7	6	3	1

Цей подвійний ряд чисел, де видно, яким чином числові значення ознаки (хі) пов'язані з кількістю їхніх повторень (р<) у даній сукупності, називається варіаційним, або рядом розподілу. Числа, з яких видно, скільки разів окремі варіанти бувають у даній сукупності, називаються частотами (вагами) варіант, їх позначають f або р. Загальна сума частот завжди дорівнює обсягу даної сукупності, тобто Z Р ^{= n}> Z ~ ^сУ^ма частот варіаційного ряду; п - обсяг сукупності вибірки.

Частоти можуть виражатися не тільки абсолютними, а й відносними числами - у частках одиниці або у відсотках від загальної кількості варіант, які утворюють дану сукупність. У таких випадках їх називають відносними

частотами (частками). Загальна сума часток дорівнює одиниці, тобто "

або » . 100 % = 100 %, якщо частоти виражені у відсотках від п. Заміна частот частками не обов'язкова, але іноді вона буває корисною, а навіть і необхідною, оскільки полегшує зіставлення (порівняння) одного варіаційного ряду з іншим, що є особливо важливим, коли порівнювані ряди відрізняються за кількістю варіант.

Для наочності відображення закону варіювання тієї чи іншої кількісної ознаки варіаційні ряди зображають у вигляді геометричних фігур у системі прямокутних координат. Наприклад, якщо з'єднати прямими лініями геометричні точки, які пов'язують значення варіант (відкладаються на осі абсцис) з їх частотами (відкладаються на осі ординат), то одержимо лінійний графік, що називається варіаційною кривою, або кривою розподілу.

Будуючи графік, на осі абсцис відкладають значення варіант, а на осі ординат - частоти. Висота перпендикулярів, яку відтворюють на осі абсцис, відповідає частотам варіант. З'єднуючи вершини перпендикулярів прямими лініями, одержують геометричну фігуру у вигляді багатокутника, яку називають полігоном розподілу частот. Наприклад, на уроках з певного навчального предмету зареєстровано самостійне виконання учнями 57 вправ у ході вивчення різних тем. Полігон розподілу частот матиме вигляд (мал. 3):

Тема	1	2	3	4	5		7	8
Частоти виконання вправ	3	5	7	10	9	15	6	2

Будь-який варіаційний ряд у загальному вигляді описується графічно варіаційною кривою, яка має не тільки ілюстративне, але й аналітичне значення, оскільки є, певною мірою, відправним пунктом статистичного аналізу мінливих ознак.

Будуючи графік варіаційних рядів, масштаби на осях координат вибирають довільно, але так, щоби висота варіаційної кривої (тобто максимальна ордината) вілносилась до її основи приблизно як 5:8.

Відкладаючи на осі абсцис класи варіаційного ряду, слід доводити їх ліворуч і праворуч до нульових класів, які не містять жодної варіанти. Недотримання цих правил, призводить до небажаних результатів: графік має шпилясту вершину та вузьку основу або надто розтягнутий по ширині. В обох випадках варіаційна крива є поганою для огляду та недостатньо чітко відображає характерні риси варіювання досліджуваної ознаки.

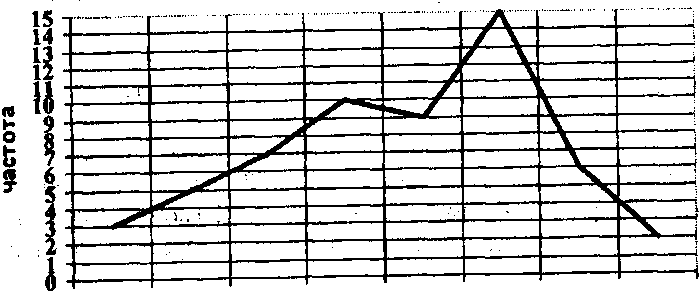
2 3 4 5 6 7 8 ознака

Рис. З

Гістограма будується аналогічно до полігона, але на осі абсцис відкладаються не відповідні окремим варіантам точки, а інтервали (відрізки) рядів варіант (мал. 4). Замість ординат, що характеризують окремі частоти, будують прямокутники з висотою пропорційною середнім значенням частот, які входять в інтервал. Якщо вибирати занадто малий інтервал, то картина буде занадто роздрібленою. При дуже великому розмірі інтервалу гістограма не покаже особливостей розподілу варіант. Наприклад, якщо вибрати при 12 оцінках (для простоти ілюстрації) інтервал завбільшки у три бали (1-3, 3-6, 6-9, 9-12), то одержимо чотири інтервальні групи. У випадку, коли прийняти, як рекомендується, нижню межу інтервалу відкритою, тобто такою, що включає граничну частоту між інтервалами, а верхню закритою, то в інтервал 1-3 оцінки не потрапляють. До інтервалу 3-6 потрапляє оцінка З, у 6-9 - оцінки 6, 7 і 8. а в інтервал 9Л2 - оцінка 11. Якщо ж є крайні оцінки, то вони беруться до уваги завжди, а для кожної інтервальної групи розраховується середня частота. У наведеному прикладі одержимо відповідно такі чотири інтервальні частоти: для першого інтервалу - 0, для другого — 1:3 = 0,33, для третього - (4 + 6 + 5):3 = 5, для четвертого - (3 + 1):3 * 1,33. Якщо побудувати для кожного інтервалу прямокутники розрахованої висоти, то утвориться гістограма розподілу оцінок, в якій Ь-частоти - повторення однакових оцінок (таблиця 11).

Таблиця IJ

Таблиця розподілу інтервалів оцінок випадку частоти розподілу кількості виконаних завдань учнями кумульовані таким чином;

Оцінки	1	2	3	4	5	6	7	8	9	10	11	12
Частоти b	-	-	1	-	-	4	6	5	3		1
Інтервал	І			II			III			IV
Сер. частоти	0:3 =0			1:3 = 0,33			(4+6+5):3 = 5			(3+1):3 = 1,33

Далі приклади інших розрахунків подані з урахуванням цього ряду таблиці.

Істотною перевагою використання полігонів € можливість накладання їх один на одний при меншому перетинанні ліній, ніж це можливо було б на гістограмах. Тому від побудованої гістограми доцільно перейти до полігона, для цього необхідно з'єднати прямими лініями середини верхніх сторін стовпчиків (рис. 4).

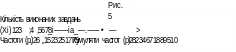
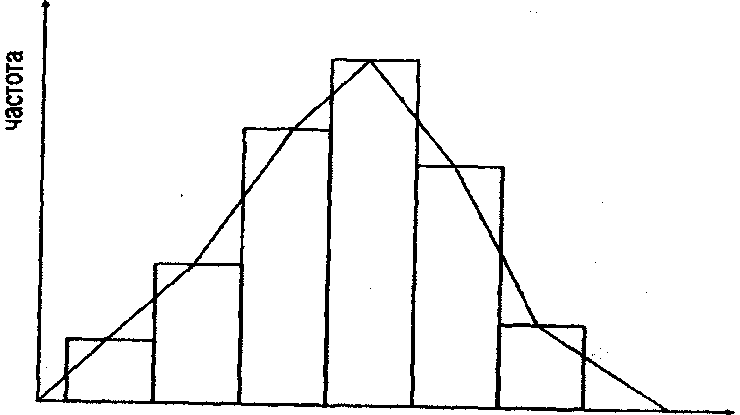
ознака

Рис. 4. Зв'язок гістограми і полігона розподілу

Крім варіаційної кривої, емпіричний ряд розподілу можна зобразити у вигляді кумуляти або огіви. Кумуляту одержують, якщо на осі абсцис відкладають значення варіант, а на осі ординат - нагромаджені частоти з наступним з'єднанням геометричних точок прямими лініями. На мал. 5 зображена кумулята розподілу завдань, виконаних учнями з використанням комп'ютера протягом півріччя. Для цього вимірювали тривалість (у хвилинах) виконання кожного завдання. На відміну від шпилястої варіаційної кривої кумулята має S-подібну форму. Нагромадження частоти одержуємо послідовним додаванням або кумуляцією частот у напрямі від мінімальної або від першої варіанти до кінця варіаційного ряду. В даному

Якщо нагромаджені частоти відкладати на осі абсцис, а значення варіант - на осі ординат з наступним з'єднанням геометричних точок прямими лініями, одержимо графік, який називається огівою.

Для огіви. та кумуляти характерна більш обтічна форма, ніж для варіаційних кривих, які, зазвичай, мають вигляд ламаної лінії. Дана властивість іноді спонукає надавати перевагу цим графікам перед емпіричною варіаційною кривою. Зокрема, огіва дає змогу порівнювати водночас декілька емпіричних розподілів неоднакового обсягу, особливо в тих випадках, коли частоти рядів виражені у відсотках від загальної кількості спостережень.