
Задача 8
Найти уравнение движения груза D или системы грузов D и Е отнеся их движение к оси х Начало отсчета совместить с положением статического равновесия. Если груз изображен штриховой линией, то он не участвует в колебательном движении, но является причиной его возникновения. В частности на схеме 1 колебания являются результатом подвеса груза Е к находящемуся в состоянии статического равновесия грузу D. На схеме 3 – наоборот: колебания являются результатом удаления груза Е от находящейся в состоянии статического равновесия системы грузов D и Е.
Если на схеме изображен символ ξ – закон движения другого конца пружины (точка В), то при исследовании колебательного движения следует рассматривать наложение свободных и вынужденных колебаний.
Таблица 8
Строка |
mD, кг |
mЕ, кг |
с1, H/м |
с2, H/м |
с3, H/м |
s, м |
ξ , м |
V0, м/c |
1 |
1 |
6 |
100 |
200 |
500 |
1 |
5sin50t |
2 |
2 |
2 |
8 |
200 |
400 |
600 |
2 |
sin100t |
3 |
3 |
3 |
7 |
300 |
200 |
700 |
3 |
10sin300t |
1 |
4 |
4 |
9 |
400 |
200 |
800 |
4 |
4sin20t |
10 |
5 |
5 |
10 |
500 |
300 |
900 |
5 |
8sin200t |
5 |
Пример решения задачи 8
В некоторый момент времени груз В
(m
=100
кг) устанавливают на плиту и отпускают
(при недеформированной пружине) без
начальной скорости. В этот же момент
времени точка D
(нижний конец пружины) начинает совершать
движение по вертикали согласно закону
ξ
= 0.5 sin20t(см)
(ось ξ
направлена вниз). Коэффициент жесткости
пружины c=
200 Н/см.
некоторый момент времени груз В
(m
=100
кг) устанавливают на плиту и отпускают
(при недеформированной пружине) без
начальной скорости. В этот же момент
времени точка D
(нижний конец пружины) начинает совершать
движение по вертикали согласно закону
ξ
= 0.5 sin20t(см)
(ось ξ
направлена вниз). Коэффициент жесткости
пружины c=
200 Н/см.
Примечание. Начало отсчета на оси x соответствует среднему положению точки В (ξ = 0).
Решение:
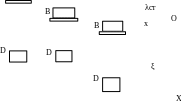 Применим
к решению задачи дифференциальные
уравнения движения точки.
Применим
к решению задачи дифференциальные
уравнения движения точки.
Рис. 8.1
Направим ось x вниз, в сторону движения груза В. (рис. 8.1) Движение груза В определяется по следующему дифференциальному уравнению:
mẍ = ∑Xi,
Таким образом,
mẍ = mg - Fупр.
Здесь
Fупр= cλ= c(λст+X – ξ),
где λ- деформация пружины,
откуда
mẍ = my – cλст – cx + cξ (1)
Статическую деформацию пружины λстнайдем из уравнения равновесия, соответствующего состоянию покоя груза В (рис. 8.2) :

B
Х
Рис.8.2
∑Xi= 0;
mg – Fупр = 0,
mg – сλст= 0,
λст = mg/c. (*)
Дифференциальное уравнение движения груза В примет вид
mẍ = mg – сmg/c – cx + c·0,5sin20t,
или после преобразования
mẍ + cx = с·0,5sin20t.
Разделив все члены уравнения на m и введя обозначения
c/m = ω2, c·0,5/m = h,
приведем дифференциальное уравнение к следующему виду:
ẍ + ω2x = hsinpt. (2)
Решение этого неоднородного уравнения складывается из общего решения x1 соответствующего однородного уравнения и частного решения x2 данного неоднородного уравнения:
x = x1 + x2.
Общее решение однородного уравнения имеет вид
x1 = С1sinωt + С2cosωt.
Тогда
x1= С1sin14t– С2cos14t,
где
ω
=
 =
= =
=
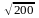 ≈ 14 рад/с
≈ 14 рад/с
Частное решение неоднородного уравнения:
x2 = h/(ω2 – p2)sinpt.
Тогда
x2=
−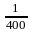 sinpt,
sinpt,
где
ω2 = 200, p2 = 400, h = 0,5.
Общий интеграл имеет вид
x = С1sin14t + С2cos14t− sin20t.
Для определения постоянных интегрирования с1 и с2 найдем, кроме того, уравнение для ẋ
ẋ
= − С114cos14t
– С2sin14t
−
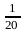 cos20t
cos20t
и используем начальные условия задачи.
Рассматриваемое движение начинается в момент ( t = 0) , когда деформация пружины является статической деформацией под действием груза В. При принятом положении начала отсчета О начальная координата груза В равна x0= −λст, причем λст = mg/c – статическая деформация пружины под действием груза В. Таким образом, при t = 0
x0 = − λст, ẋ= 0.
Составим уравнения x = x(t) и ẋ = ẋ(t) для t = 0:
ẋ= 14С1 − ; x0 = С2,
откуда
С1=
 ,
С2
= − λст.
,
С2
= − λст.
Найдем числовые значения входящих в уравнение величин:
ω
=
 =
=
≈
14 рад/с;
=
=
≈
14 рад/с;
λст=
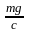 =
=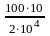 =
0,05 м;
=
0,05 м;
 =
=
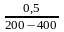 =
-
м;
=
-
м;
Следовательно, уравнение движения груза В
x= 0,003sin14t – 0,05cos14t – 0,0025sin20t (м).
1 x 

|
2 |
3 |
4 |
5 B 

|
6 |
7 |
8 |
9 |
1 |
1 |
1 x  2
2
|
1 c3 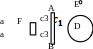 3
3
|
1 |
1 |
16 |
17 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |

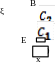
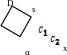



 0
0 1
1
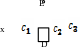 4
4
 5
5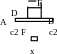 8
8 9
9 0
0 1
1 2
2 3
3 4
4