3. Динамика Задача 7
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости. Найти скорость шарика в положениях В, С, D и давление шарика на стенку трубки в положении С. Трение на криволинейных участках траектории не учитывается. В схемах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь h0, отделяется от пружины. Необходимые для расчета данные приведены в табл.7. Приняты следующие обозначения: m – масса шарика, vA - начальная скорость шарика, τ - время движения на участке АВ или на участке ВD (схемы 3, 4, 9-13, 15-17, 22), f - коэффициент трения скольжения шарика по стенке трубки, h0 - величина начального сжатия пружины, с – коэффициент жесткости пружины, H - наибольшая высота подъема шарика.
Таблица 7
Строка |
m, кг |
VA , м/c |
f
|
τ, c |
α, град |
β, град |
c, Н/м |
h0, м |
1 |
1 |
2 |
0,1 |
3 |
30 |
15 |
100 |
0,1 |
2 |
2 |
10 |
0,2 |
1 |
45 |
30 |
200 |
0,2 |
3 |
3 |
5 |
0,3 |
2 |
60 |
45 |
50 |
0,3 |
4 |
0,5 |
15 |
0,4 |
5 |
15 |
60 |
30 |
0,01 |
5 |
0,1 |
0 |
0,15 |
4 |
75 |
0 |
80 |
0,05 |
Пример решения задачи 7
Дано:
m = 0,8 (кг), vA = 5 (м/c), R = 0,6 (м) τ = 0,3 (с), f = 0,15, α = 30°
Найти:
vB, vC, vD, NC, tDE
Решение:
Согласно теореме об изменении количества движения для материальной точки на участке АВ (рис.7.1):
Откуда:
Рис.7.1
Для
определения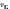 
и 
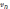применим теорему об изменении кинетической
энергии материальной точки:
=
=
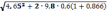= 6,6 м/с.
= 
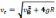= 6,72 м/с.
Реакцию
определим с помощью уравнения движения
в проекции на нормаль (естественная
ось):
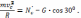
Выражаем:
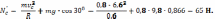
По теореме об изменении кинетической энергии:
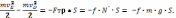
Откуда:
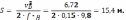
Для равноускоренного движения:
Ответ:
1 |
|
|
|
|
|
|
D |
|
|
|
2R |
C |
S A 
|
|
|
|
|
А |
|
α 21 
|
|
α Н 
|
С 
|
