Задача 3

Имеется однородная плита весом G=1 кН с размерами а = 1 м, b = 2 м, c = 2 м, d = 1 м (рис.3.1). Плита закреплена горизонтально посредством шести прямолинейных стержней с шарнирами на концах и имеет отверстие. На плиту действует сила Р=2 кН вдоль стороны АВ и сила тяжести G, направленная вертикально вниз. Определить реакции стержней (усилия в стержнях), поддерживающих горизонтальную однородную плиту с отверстием. Данные взять из табл.3.

Таблица 3

Строка	a, м	b, м	c, м	d, м	Ø, м
1	1	2	4	0,2	0,5
2	3	4	6	0,3	2
3	2	6	8	0,4	1
4	10	10	8	1	4
5	6	8	4	2	3

Пример решения задачи 3

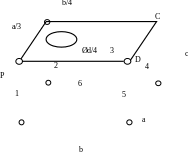
Рис. 3.1.

Решение:

Координаты центра тяжести плиты (т. К) определяются по формулам:

.

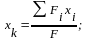
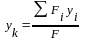Чтобы воспользоваться этими формулами, фигуру делим на отдельные части, положения центров тяжести которых известны.

Рис. 3.2.

В данном случае такими являются: 1 – прямоугольник, 2 – круг. Площадь, круга вырезанной из прямоугольника считаем отрицательной. Положение центров тяжести этих фигур известно и определяется точками: C₁ (x₁; y₁); C₂ (x₂; y₂) Согласно рис.3.2 x₁=1; y₁=0,5; x₂=0,5; y₂= 0,67.

– площадь прямоугольника, – площадь круга.

F₁ = 1∙ 2 = 2 м²

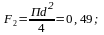
Тогда

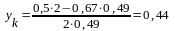
Изобразим расчётную схему для плиты с целью определения реакций стержней (рис.3.3.). Реакции направлены вдоль стержней.

y

Рис. 3.3.

Согласно приведённым на рис. 3.1 размерам можно составить следующие выражения.

sinα = cosα = sinγ = cosγ = 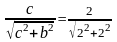= 0,71 (α = γ = 45⁰);

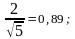
Составим уравнения равновесия для плиты ABCD(рис. 3.3)

1. ƩFkx = 0

-N₆cosγ + N₃cosα = 0

N₆ = N₃

2. ƩFky = 0

P + N₄cosβ = 0

4,44кН

3. ƩM_z (F_k) = 0

-N₃ cosα ∙a + α + N₄ cosβ ∙b = 0

-N₃0,71 ∙ 1 + N₄0,45 ∙2 = 0

N₃ = 1,27N₄ = 1,27 ∙ ( -4,44) = - 5,64 кН

4. ƩM_x (F_k) = 0

-N₂ ∙a – N₃sinα ∙a – G ∙y_k = 0

N₂ = -N₃ sinα – G ∙y_k = 5,64∙0,71 - 1∙0,44 = 3,56 кН

5. ƩM_y (F_k) = 0

N₅∙ b + N₆sin γ ∙ b+ N₄sinβ ∙b + G ∙x_k = 0

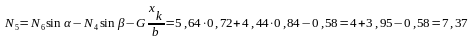
6. ∑Fkz = 0

-N₁- N₂ – N₅ – G – N₃ sinα – N₆ sinγ – N₄ sinβ = 0

N₁ = - N₂ – N₅ – G - N₃ sinα - N₆ sinγ - N₄ sinβ = - 3,56 – 7,37 – 1 + 5,64 ∙0,71 + 4,44 ∙ 0,82 = - 3,56 – 7,37 – 1 + 4 + 4 + 3,95 = 0 кН

Проверка:

ƩM_y1(F_k) = 0

-N₁ ∙ b+ N₂ ∙ b+ N₃ sinα ∙ b + G ( b – x_k) = 0

3,56 ∙ 2 – 5,64 ∙0,71 ∙ 2 + 1 ∙ 0,84 = 0

7,12 – 8 + 0,84 = 0

7,96 – 8 = 0

_{О ценим величину погрешности, если эта величина превышает точность инженерных расчётов (ε > 3%), то правильность записанных ранее формул и вычислений необходимо проверить. В нашем случае величина погрешности составляет}

_{Это позволяет сделать вывод о правильности сделанных расчётов.}