2. Порядок проведения работы

На карданные валы действует крутящий момент, передаваемый от коробки передач, и осевые силы, возникающие при колебаниях ведущего моста на рессорах.

При увеличении скорости вращения могут возникнуть поперечные колебания карданного вала.

Поперечный изгиб вала происходит за счет центробежных сил, возникающих вследствие несовпадения оси вращения вала с его центром тяжести.

Несовпадение может иметь место за счет неизбежных неточностей изготовления, прогиба вала под действием собственного веса и других причин.

В данной работе расчет карданной передачи производится по максимальному крутящему моменту, развиваемому двигателем – M_max при движении автомобиля на первой передаче, когда крутящий момент, передаваемый через трансмиссию, максимален (передаточное число первой передачи i₁ ).

1. Определение напряжения кручения и угла закручивания карданного вала

Максимальное напряжение кручения вала, определяется для случая приложения максимального момента двигателя и при действии динамических нагрузок. Действие динамических нагрузок учитывается коэффициентом динамичности: K_Д = 1…3.

Момент сопротивления кручению :

(1.1.)

где – постоянная величина ( ) ;

D – наружный диаметр вала карданной передачи ;

d – внутренний диаметр вала карданной передачи .

Максимальное напряжение кручения вала :

(1.2.)

где – максимальный крутящий момент двигателя ;

– передаточное число первой передачи ;

– коэффициентом динамичности ;

– момент сопротивления кручению .

Величина угла закручивания вала :

(1.3.)

где – максимальный крутящий момент двигателя ;

– передаточное число первой передачи ;

l – длина карданного вала ;

– коэффициентом динамичности ;

– постоянная величина ( ) ;

G – модуль упругости при кручении, ( G = 8,510¹⁰ Па);

– момент инерции сечения вала при кручении.

Момент инерции сечения вала при кручении :

(1.4.)

где – постоянная величина ( ) ;

D – наружный диаметр вала карданной передачи ;

d – внутренний диаметр вала карданной передачи .

Величина угла закручивания единицы длины карданного вала :

_, (1.5.)

где – величина угла закручивания вала ;

l – длина карданного вала .

2. Определение осевой силы, действующей на карданный вал

Кроме крутящего момента, на карданный вал действуют осевые силы Q, возникающие при перемещениях ведущего моста.

Задний мост при движении автомобиля по неровностям совершает качание относительно оси серьги рессоры по некоторому радиусу R₁.

Карданный вал колеблется вокруг центра карданного шарнира, которым он соединяется со вторичным валом коробки передач по некоторому радиусу R₂.

Вследствие неравенства этих радиусов совершаются осевые перемещения карданного вала. Величина осевых перемещений на преобладающих режимах эксплуатации составляет 2-5 мм.

Величина осевой силы действующей на карданный вал при колебаниях автомобиля :

, (1.6.)

где – максимальный крутящий момент двигателя ;

– передаточное число первой передачи;

 – коэффициент трения в шлицевом соединении.

– диаметры шлицев по выступам;

– диаметры шлицев по впадинам.

Коэффициент  зависит от качества смазки. При хорошей смазке  = 0,04…0,6 ; при плохой смазке  = 0,11…0,12 . В случае заедания  = 0,4…0,45 ;

Тогда осевые силы будут рассчитываться :

при хорошей смазке (  = 0,04…0,6 ) , (1.7.)

при плохой смазке (  = 0,11…0,12 ), (1.8.)

при заедании (  = 0,4…0,45 ) . (1.9.)

Осевые усилия, возникающие в карданной передаче, нагружают подшипники КП и главной передачи. Снижение осевой нагрузки будет иметь место при наличии соединения, в котором трение скольжения при осевом перемещении будет трением качения (шлицы с шариками).

3. Расчет крестовины карданного шарнира.

Расчетная схема крестовины представлена на рисунке 1.4.

На шип крестовины карданного шарнира действует сила Р.

Величина силы действующей на шип крестовины карданного шарнира:

(1.10.)

где – максимальный крутящий момент двигателя ;

– передаточное число первой передачи ;

R – расстояние от оси крестовины до середины шипа .

Сила Р действует на шип крестовины, вызывая его смятие, изгиб и срез. Напряжение смятия шипа не должно превышать 80 МПа, напряжение изгиба – 350 МПа, напряжение среза – 170 МПа.

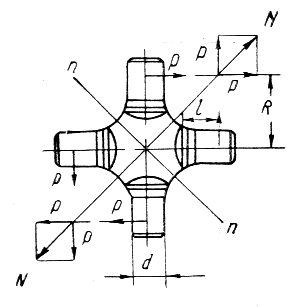
Рис. 1.4. Расчетная схема крестовины карданного шарнира

Напряжение смятия определяется:

(1.11.)

где P – величина силы действующей на шип крестовины карданного шарнира ;

– диаметр шипа ;

– длина шипа .

Момент сопротивления изгибу сечения шипа крестовины:

(1.12.)

где – постоянная величина ( ) ;

– диаметр шипа.

Напряжение изгиба:

(1.13.)

где P – величина силы действующей на шип крестовины карданного шарнира ;

– длина шипа ;

W – момент сопротивления изгибу сечения шипа крестовины .

Напряжение среза :

(2.14.)

где P – величина силы действующей на шип крестовины карданного шарнира ;

– постоянная величина ( ) ;

– диаметр шипа .

Силы Р, приложенные к шипам, также дают равнодействующую N, которая вызывает напряжения растяжения в сечении n-n. Для крестовины карданного шарнира площадь сечения, в котором возникают эти напряжения, F .

Растягивающие напряжения:

(1.15.)

где P – величина силы действующей на шип крестовины карданного шарнира ;

F – площадь сечения крестовины карданного шарнира .

Допускаемое напряжение на растяжение составляет 120 МПа.