2.3. Лабораторная работа № 13
Метод прогонки для уравнения теплопроводности
2.3.1. Методические указания
Для уравнения теплопроводности
(3.1)
с граничными условиями
;
;
;
(3.2)
строится сетка с шагами h и k:
;
(i,j=0,1,2…).
Шаблон выбирается в виде неявной схемы (рисунок 2.2)
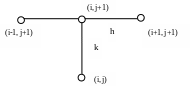
Рисунок 2.2
Дифференциальное уравнение (3.1) заменяется конечно-разностными уравнениями в соответствии с выбранным шаблоном.
,
(3.3)
где
-
масштабный коэффициент для шагов h и k.
При этом граничные условия (3.2) принимают вид
;
.
(3.4)
Метод
прогонки позволяет работать с ненулевыми
элементами трехдиагональной матрицы
системы уравнений (3.2); (3.3). Здесь
осуществляется прямой ход для определения
вспомогательных коэффициентов
;
и обратный ход для получения решения
.
Для начала прямого хода коэффициенты считаются по формулам
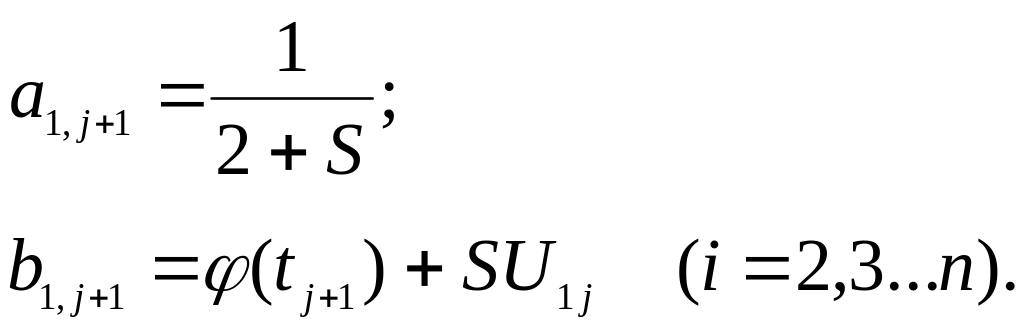
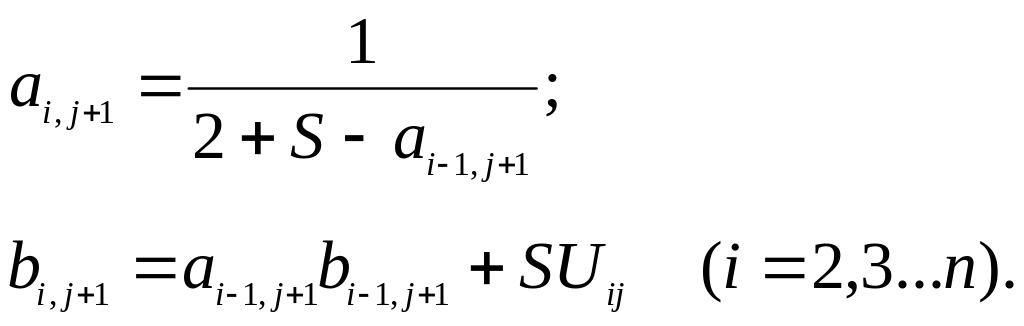(3.5)
Для обратного хода вычисление функции
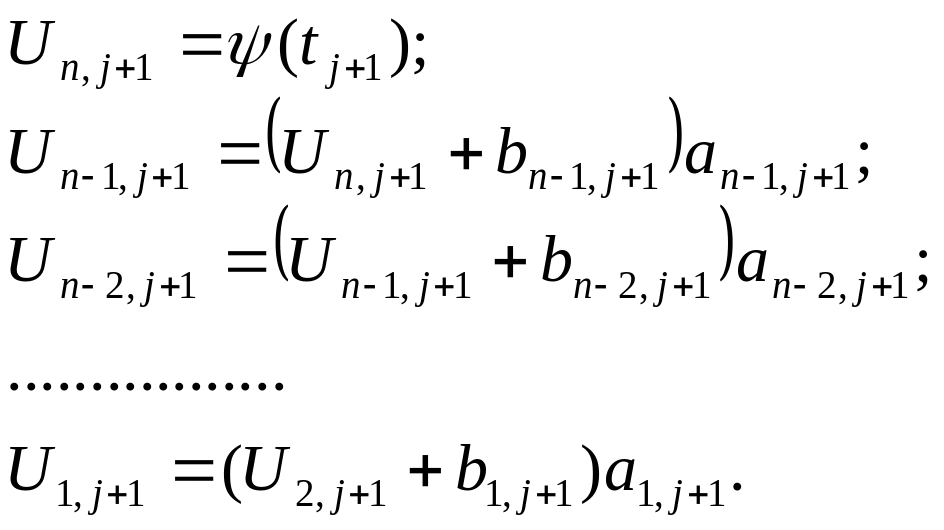(3.6)
Вычисленные значения по (3.6) дают таблицу решения для одного слоя.
2.3.2. Порядок выполнения работы
1. В соответствии с заданным вариантом табл. 2.3 составьте программу метода прогонки и подготовьте данные.
2. Проведите расчет и получите таблицу решений.
3. Ответьте на вопросы:
1. В чем преимущество метода прогонки?
2. Как выбрать масштабный коэффициент?
3. Каково условие устойчивости данной схемы метода прогонки?
4. Как выполняется прямой и обратный ход, по слоям оси y или сразу на всем отрезке оси y?
Таблица 2.3
№ варианта |
|
|
|
1 |
|
0 |
|
2 |
|
|
0,932 |
3 |
|
|
|
4 |
|
|
|
5 |
|
0 |
|
6 |
|
0,2 |
|
7 |
|
|
0,354 |
8 |
|
|
|
9 |
|
0,2 |
|
10 |
|
|
0,581 |
11 |
|
|
|
12 |
|
|
|
13 |
|
0,3 |
|
14 |
|
0,939 |
|
15 |
|
|
0,844 |
2.4. Лабораторная работа № 14
Метод Монте-Карло
2.4.1. Методические указания
Рассматривается уравнение Лапласа
(4.1)
в области G , представляющей квадрат ABCD с вершинами A(0,0); B(0,2); C(2,2); D(2,0).
Шаг h=0,2. На область G накладывается сетка
;
(i,j=0,1,2…).
В методе моделируются случайные блуждания части по узлам сетки, пока она не попадет на границу области . Случайные блуждания генерируются датчиком случайных чисел 0÷9. Таблица генерации приведена в табл. 2.4.
Таблица 2.4
Случайное число |
Перемещение |
Описание перемещений |
0 4 1 5 2 6 3 7 8 9 |
|
Шаг вправо Шаг вверх Шаг влево Шаг вниз Частица на месте |
При достижении границы заданной области фиксируется значение функции на границе.
При переходе от дифференциального уравнения (4.1) к конечно-разностному для определения функции в узлах сетки внутри области G применялась схема
;
(4.2)
,
где
- значение функции в граничной точке
(p,q).
Искомые
неизвестные
можно рассматривать как математическое
ожидание функции
на
границе
для траекторий блуждающей точки
,
начинающей блуждание в точке (i,j)
и принимающей значение
в граничной точке.
Замена математического ожидания эмпирическим дает формулу
,
(4.3)
где (p,q) – граничные точки;
N
– количество блужданий для точки
,
которая начала блуждание в (i,j)
и закончила в
.
После проведения N блужданий для данного узла сетки рассчитывается значение функции в этом узле по (4.3). Для расчета не требуется значение функции в соседних точках.
2.4.2. Порядок выполнения работы
1. Составьте программу метода Монте-Карло задайте число выриантов блужданий для каждого внутреннего узла сетки. В программе используйте датчик случайных чисел.
2. Используя таблицу 2.1 проведите расчет, получите таблицу решений.
3. Ответьте на вопросы
1. Какие достоинства и недостатки метода Монте-Карло?
2. Является ли метод самостартующим?