2.2. Лабораторная работа № 12

Процесс Либмана в методе сеток

2.2.1. Методические указания

Аналогично предыдущему уравнению в частных производных заменяются на конечно- разностные, для уравнения Лапласа (1.1) они имеют вид

, (2.1)

где k – номер итерации при применении метода Зейделя для решения системы алгебраических уравнений для внутренних точек области решения.

Таблица 2.1

№ варианта	U/AB	U/BC	U/CD	U/AD
1	0			0
2
3			0
4
5		0
6			40	50
7				0
8			20
9
10
11				0
12
13				0
14	0
15

Для граничных узлов сетки значения функции U уточняются по формулам линейной интерполяции (рисунок 2.1)

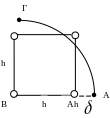
Рисунок 2.1

;

, (2.2)

где А – ближайшая точка к Ah на границе Г;

U(A) – заданное граничное условие;

В – ближайший к Ah внутренний узел сетки;

- удаление узла Ah от граничной точки A;

k – номер итерации.

При этом принимает значения:

>0, если Ah внутренняя точка заданной области решения G;

<0, если Ah внешняя точка G;

=0, если Ah на границе Г.

Для выбора начального приближения можно задать любые числа в пределах, допустимых по принципу максимума.

Коррекция значений функции U в узлах (2.2) входит в процесс итерации, который осуществляется по методу Зейделя для решения системы алгебраических уравнений (2.1).

Процесс Зейделя заканчивается, если

,

где - заданная точность.

2.2.2. Порядок выполнения работы

1. Подготовьте программу для решения уравнения Лапласа (1.1) с заданными граничными условиями в табл. 2.2 с начальным шагом h=0,1.

2. Получите таблицу решения с точностью до =0,01, выполняя процесс Либмана.

3. Ответьте на вопросы:

1. Какова оценка погрешности в методе Либмана?

2. В чем достоинство метода Либмана?

3. Как организован в программе цикл для формул (2.1) и (2.2)?

4. Какой шаблон выбран для составления алгебраических уравнений для внутренних точек?

Таблица 2.2

№ варианта	Граница	Значение на границе
1	,
2
3
4	,
5
6
7
8
9
10
11
12
13
14
15