1.10. Лабораторная работа № 10
Метод коллокации
1.10.1. Методические указания
Метод коллокации относится к приближенным проекционным методам, применяется к граничной задаче
;
(10.1)
(10.2)
В качестве решения берется линейная комбинация базисных функций:
,
(10.3)
так что
(10.4)
Выбранное решение подставляется в дифференциальное уравнение (10.1) и определяется невязка
.
(10.5)
Подбираются такие ci , чтобы невязка обращалась в нуль в выбранных точках заданного интервала, которые называются точками коллокации. Получается система уравнений для определения коэффициентов ci.
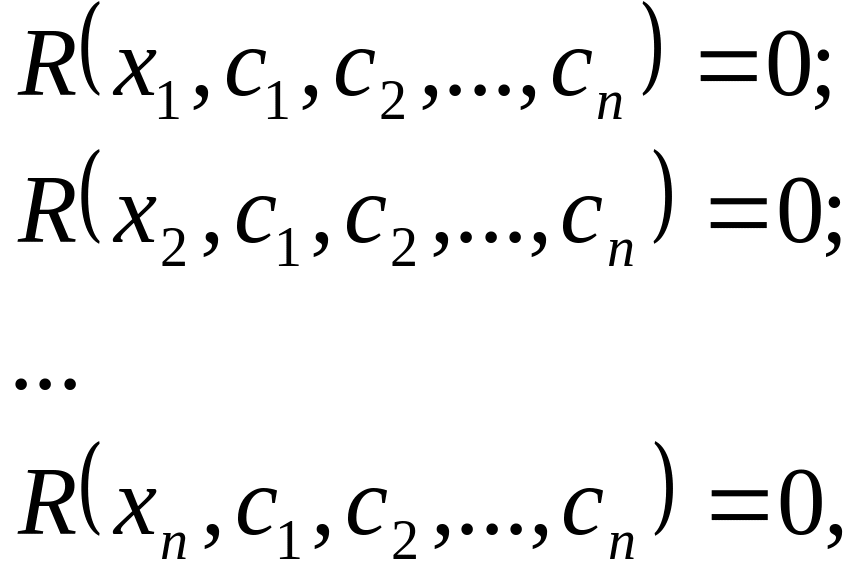(10.6)
где xi - выбранные точки коллокации.
После решения системы уравнений найденные ci подставляются в решение (10.3).
1.10.2. Порядок выполнения работы
1. Составьте программу метода коллокации со следующими своиствами:
базисные функции задаются с терминала, они должны быть линейно независимые и в соответствии с граничными условиями удовлетворять требованиям (10.4);
точки коллокации также задаются с терминала, их количество должно совпадать с n – количеством ci коэффициентов в сумме решения (10.3);
в зависимости от количества точек коллокации формируется система алгебраических уравнений (10.6) для определения ci;
решение получается в виде функции приближения (10.3), разбив интервал аргумента несколькими узлами, вычисляют по функции (10.3) таблицу решения;
заданная точность решения
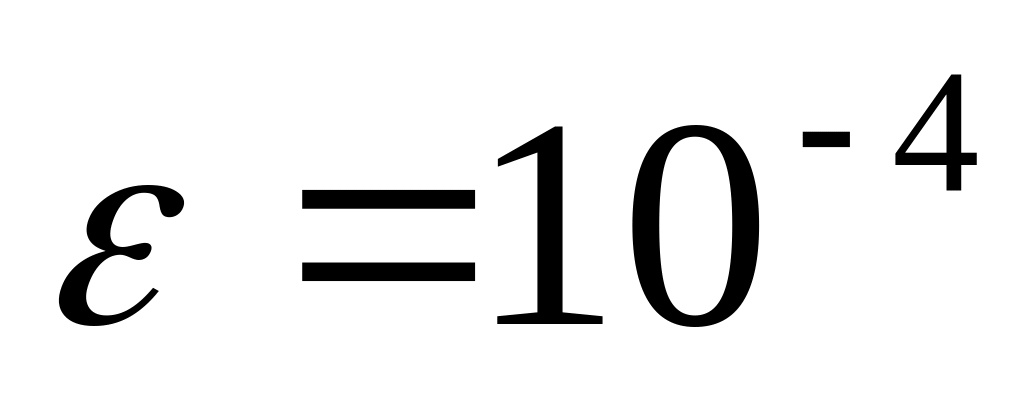достигается сравнением решений при n
слагаемых в (10.3) и n
+1 слагаемых, если они отличаются меньше,
чем на
,
то можно ограничиться таким рядом.
2. Получите решение в соответствии с вариантом табл. 1.5, получите приближенное решение в виде функции и таблицу решений.
3. Ответьте на вопросы:
1. Какими свойствами должны обладать базисные функции? Какие функции выбраны?
2. Что такое точки коллокации?
3. Как выдержать заданную точность решения?
Таблица 1.5
Вари-анты |
Уравнение |
f(x) |
Граничные условия |
Указания по точкам коллокации |
1 2 3 4 5 6 7 8 |
|
|
|
|
9
10
11
12 |
|
|
|
|
13 14 15 |
|
0 x
|
|
|
Часть 2. Уравнения в частных производных
2.1. Лабораторная работа № 11
Метод сеток
2.1.1. Методические указания
Метод сеток применяется для решения задачи Дирихле уравнения Лапласа
.
(1.1)
В данной работе решение определяется в квадрате ABCD с вершинами A(0,0), B(0,1), C(1,0), D(1,1) при шаге h=0,1. Граничные условия задаются функциями, приведенными в табл. 2.1.
Область решения покрывается сеткой с заданным шагом h:
;
, (i,j=0,1,2…n)
b1 вычисляются решения на граничном контуре Г по заданной в таблице функции.
Уравнение Лапласа (1.1) заменяется конечно-разностным путем замены производных конечными разностями
,
(1.2)
т.е. Uij определяется как среднее значение четырех соседних точек. Составляется подобное уравнение для каждой внутренней точки.
Полученную систему алгебраических уравнений решают методом Зейделя или методом Гаусса.
2.1.2. Порядок выполнения работы
1. Составьте программу для получения системы конечно-разностных уравнений в соответствии с вариантом задания. В программе должны быть вычислены также функции на границе Г, получено решение методом Гаусса. Исходные данные в табл. 2.1.
2.
Отладьте программу и проведите расчет
таблицы решений с точностью
.
Погрешность приближенного решения
обеспечивается просчетом с шагом h и
шагом h /2 и
применением правила Рунге
.
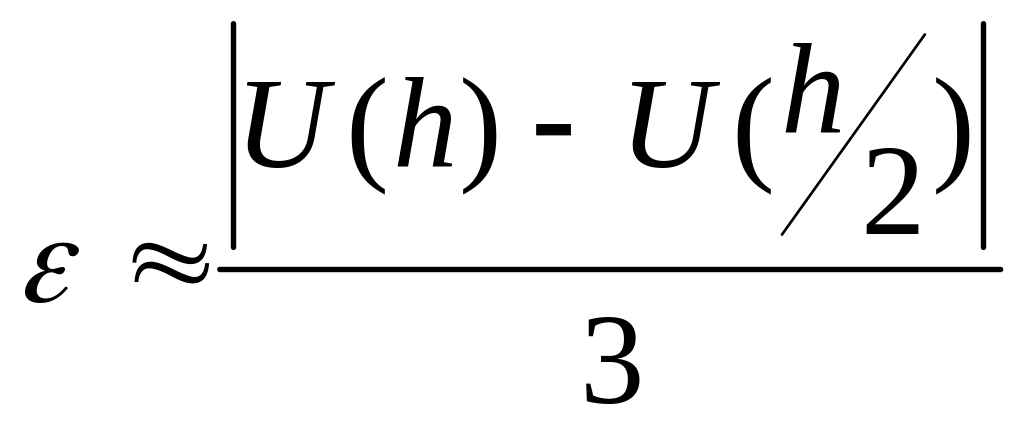(1.3)
3. Ответьте на вопросы:
1. Из каких составляющих состоит погрешность решения?
2. Как оценить погрешность?
3. Какие шаблоны применялись в работе данного метода?