Часть 3. Интегральные уравнения

3.1. Лабораторная работа № 17

Метод последовательных приближений для интегральных уравнений

3.1.1. Методические указания

Для уравнения Фредгольма

(1.1)

решения определяются в виде ряда

. (1.2)

Функции определяются последовательной системой

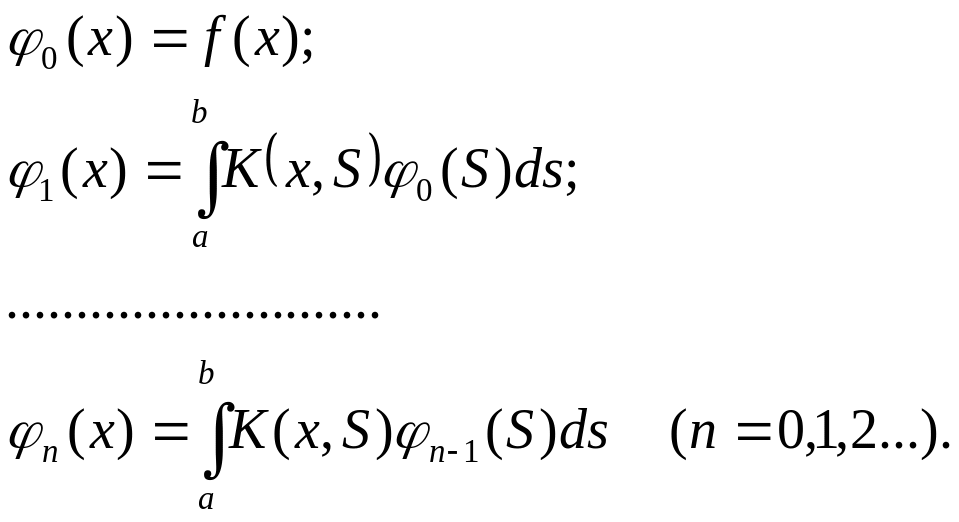(1.3)

Квадратуры вычисляются одним из численных методов интегрирования.

Ряд (1.2) сходится не при любых значениях , поэтому требуется определение радиуса сходимости.

Оценка точности решения при нескольких членах ряда может быть выполнена сравнением значений двух соседних последних слагаемых ряда.

3.1.2. Порядок выполнения работы

1. В соответствии с заданным вариантом табл. 3.1 подготовить программу последовательных приближений. Проверить, будет ли сходиться ряд (1.2) при заданных , если ряд не сходится, то надо искать в радиусе сходимости.

Отрезок [a, b] взять [0, 1].

Для вычисления приближенного решения ограничиться несколькими слагаемыми ряда в соответствии с выбранным .

2. Проведите расчеты, получите приближенное решение и таблицу решений.

Определите границу сходимости метода.

3. Ответьте на вопросы:

1. Как оценить погрешность на n-м шаге?

2. Как определить радиус сходимости?

3. Каковы недостатки метода?

4. Что такое итерированное ядро?

Таблица 3.1

№ варианта
1		1
2	1
3
4
5
6			1
7	1
8
9	1
10	1		1
11
12
13
14
15			1

3.2. Лабораторная работа № 18

Метод конечных сумм для интегральных уравнений

3.2.1. Методические указания

Интегральное уравнение Фредгольма

(2.1)

сводится к конечно-разностным уравнениям разбиением отрезка [a, b] точками

, (i,j=0,1,2…)

где h – выбранный шаг.

Интеграл в (2.1) заменяется квадратурной формулой.

Тогда получаем систему уравнений

(2.2)

где - коэффициенты Ньютона - Котеса при замене интеграла квадратурными формулами;

.

Выбрав одну из квадратурных формул, можно получить систему уравнений относительно , решив которую, получим таблицу решения для интегрального уравнения.

3.2.2. Порядок выполнения работы

1. В соответствии с заданным вариантом табл. 3.1 составьте программу метода конечных сумм. Для приближенного представления интеграла используйте квадратурную формулу Симпсона на отрезке [0, 1], шаг выбрать самостоятельно.

Решение полученной системы дает таблицу решений, а также приближенное решение в соответствии с (2.2).

2. Проведите расчет и получите конечный результат в двух видах.

3. Ответьте на вопросы:

1. На сколько частей разбит отрезок [a, b]?

2. Из каких условий выбираются коэффициенты квадратурных формул ?

3. Что такое собственное значение ядра?

4. При каких условиях метод дает хорошие результаты?