Министерство образования и науки

Российской Федерации

Рубцовский индустриальный институт (филиал)

ГОУ ВПО «Алтайский государственный технический

университет им. И.И. Ползунова»

А.Г. Лебедев

Лабораторный практикум

по численным методам

в дифференциальных уравнениях

Методические указания и задания к лабораторным работам

для студентов специальности «Прикладная математика»

Рубцовск 2011

УДК 681.3

Лебедев А.Г. Лабораторный практикум по численным методам в дифференциальных уравнениях: Методические указания и задания к лабораторным работам для студентов специальности «Прикладная математика» / Рубцовский индустриальный институт. Рубцовск, 2011. – 45 с.

Рассмотрены приближенные методы численного решения обыкновенных дифференциальных уравнений, уравнений в частных производных, а также интегральных уравнений.

Приведены методические указания и задания для разработки программ, которые подготавливаются студентами на лабораторном практикуме.

Методические указания предназначены для студентов специальности «Прикладная математика», а также могут быть использованы студентами и аспирантами других специальностей для решения дифференциальных уравнений.

Рассмотрены и одобрены

на заседании кафедры ПМ

Рубцовского индустри-

ального института.

Протокол № 3 от 16.11.10.

Рецензент: к.ф.–м.н., зав. кафедрой «ВМФиХ» Г.А. Кириллова

 Рубцовский индустриальный институт, 2011

СОДЕРЖАНИЕ

Введение	4
ЧАСТЬ 1. Обыкновенные дифференциальные уравнения	5
1.1. Лабораторная работа № 1. Метод последовательных приближений	5
1.2. Лабораторная работа № 2. Метод Эйлера	7
1.3. Лабораторная работа № 3. Метод Рунге-Кутта	8
1.4. Лабораторная работа № 4. Метод Рунге-Кутта для систем уравнений	10
1.5. Лабораторная работа № 5. Метод Адамса	12
1.6. Лабораторная работа № 6. Метод Милна	13
1.7. Лабораторная работа № 7. Метод конечных разностей	14
1.8. Лабораторная работа № 8. Метод прогонки	16
1.9. Лабораторная работа № 9. Метод стрельбы	18
1.10. Лабораторная работа № 10. Метод коллокации	21
ЧАСТЬ 2. Уравнения в частных производных	23
2.1. Лабораторная работа № 11. Метод сеток	23
2.2. Лабораторная работа № 12. Процесс Либмана в методе сеток	24
2.3. Лабораторная работа № 13. Метод прогонки для уравнения теплопроводности	27
2.4. Лабораторная работа № 14. Метод Монте-Карло	29
2.5. Лабораторная работа № 15. Метод Ритца	31
2.6. Лабораторная работа № 16. Метод конечных элементов	34
ЧАСТЬ 3. Интегральные уравнения	38
3.1. Лабораторная работа № 17. Метод последовательных приближений для интегральных уравнений	38
3.2. Лабораторная работа № 18. Метод конечных сумм для интегральных уравнений	40
3.3. Лабораторная работа № 19. Метод коллокации для интегральных уравнений	41
3.4. Лабораторная работа № 20. Метод моментов	42
СПИСОК ЛИТЕРАТУРЫ	44

Введение

Настоящие методические указания предназначены для организации лабораторных работ по численным методам для решения дифференциальных обыкновенных уравнений, уравнений в частных производных второго порядка и интегральных уравнений. Задания и методические указания предусматривают самостоятельную подготовку студентами программного обеспечения по каждому методу в соответствии с индивидуальными заданиями.

Часть 1. Обыкновенные дифференциальные уравнения

1.1. Лабораторная работа № 1

Метод последовательных приближений

1.1.1. Методические указания

Метод последовательных приближений для задачи Коши

(1.1)

заключается в замене ее на интегральное уравнение

.

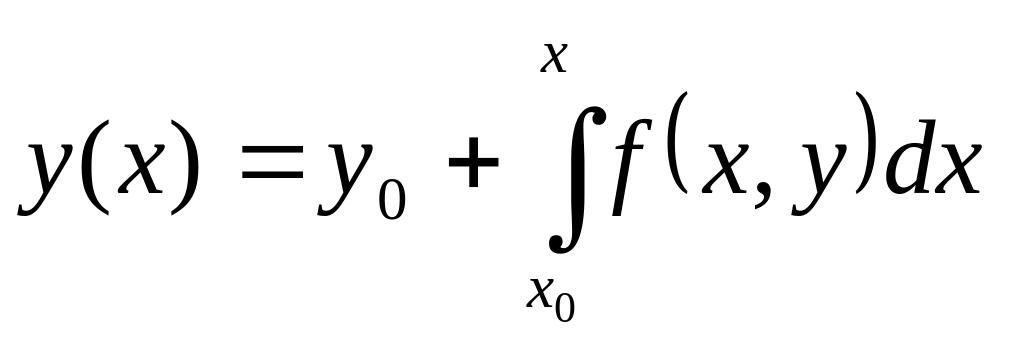Для его решения применяются последовательные приближения в виде итерационного процесса

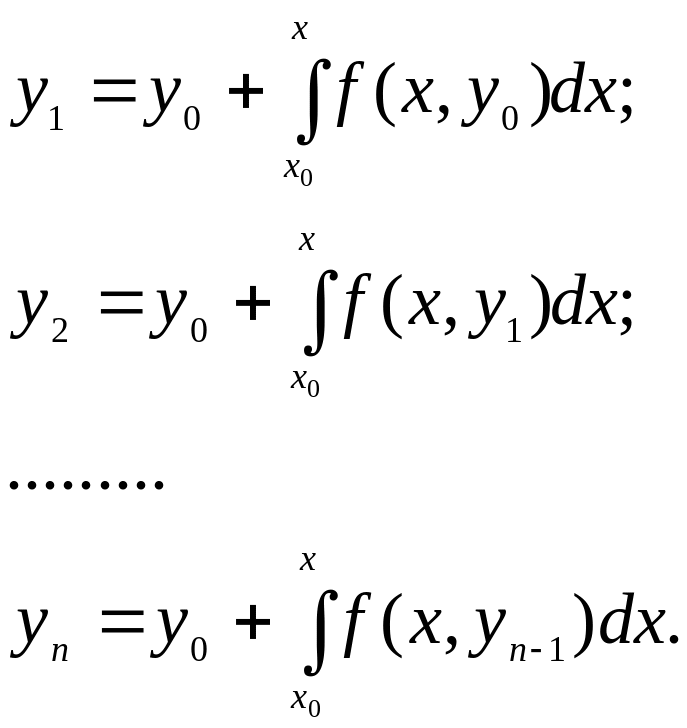(1.2)

Для численного процесса отрезок, на котором рассматривается решение, разбивается на участки с шагом h:

.

Для вычисления интегралов применяется кубатурная формула

, (i=1,2,…m) (1.3)

где вычисляется по ,

m – количество отрезков разбиения заданного интервала.

Коэффициенты определяются из условия, чтобы формула была точной для полинома степени не выше m+1, и имеют различные значения при различном разбиении заданного интервала.

Для случая m=4, т.е. разбиение на 4 части, формулы для 4 точек имеют вид:

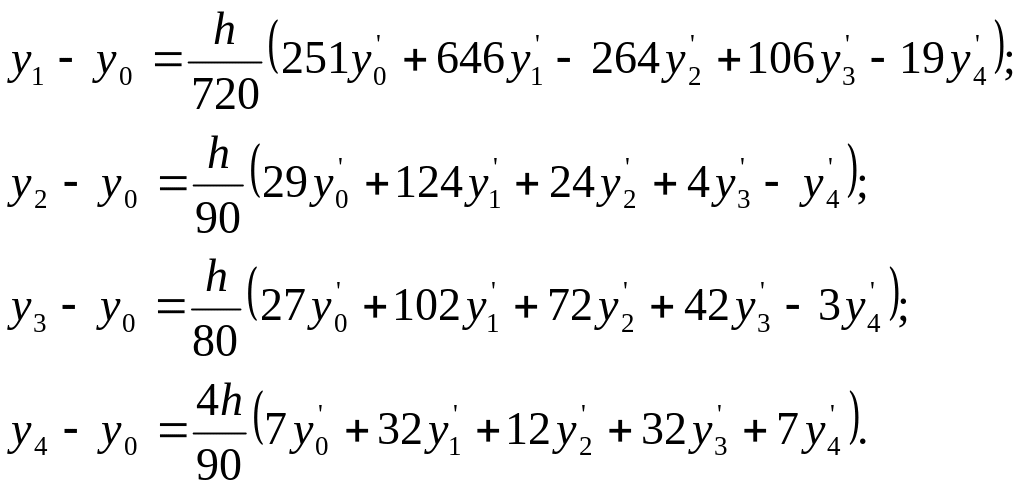(1.4)

Последовательные приближения вычисляются по формулам

. (1.5)

Подстановки ; ; ; в правую часть (1.4) дают новое приближение . Производные вычисляются через , = .

1.1.2. Порядок выполнения работы

1. Составьте программу метода последовательных приближений с разбиением интервала на 4 отрезка.

2. Проведите расчет в соответствии с вариантом табл. 1.1 с точностью .

3. Ответьте на вопросы:

1. Из каких соображений выбираются коэффициенты кубатурной формулы (1.3) ?

2. Каковы условия сходимости метода последовательных приближений?

3. Как оценить погрешность на n-м шаге приближения? Как выдержать заданную точность приближения?

4. Как выбрать начальное приближение?

Таблица 1.1

Вариант	Уравнение
	;
	;
	;
	;
	;
	;
	;
	;
	;
	;
	;
	;
	;
	;
	;

1.2. Лабораторная работа №2

Метод Эйлера

1.2.1. Методические указания

Метод Эйлера применяется для решения задачи Коши.

. (2.1)

Выбирается шаг h на заданном интервале аргумента для построения системы точек

Производную в уравнении (2.1) заменяем на приближенное значение

,

и итерационный процесс строится по схеме

(2.2)

где i – номер точки разбиения отрезка.

Метод Эйлера с уточнением заключается в том, что начальное приближение строится по формуле (2.2), а затем по формуле уточнения

. (2.3)

Уточнение (2.3) продолжается до тех пор, пока в пределах заданной точности два последовательных приближения и , если алгоритм уточнения численного значения после 3-х, 4-х итераций не приведет к совпадению требуемых значений, тогда уменьшаем h (шаг) вычисления.

1.2.2. Порядок выполнения работы

1. Составьте программу метода Эйлера с уточнением. Исходные данные содержатся в табл.1.1., шаг h=0,1, =0,01.

2. Введите данные, получите таблицу решений, в программе установите счетчик итераций.

3. Ответьте на вопросы:

1. Каков порядок ошибки метода?

2. В чем разница основного метода Эйлера и метода с уточнением?

3. В чем недостатки и преимущества метода?

4. Является ли метод Эйлера самостартующим?

5. Является ли метод Эйлера с уточнением одношаговым?

6. Каков геометрический смысл метода Эйлера?