Алгоритм решения задачи № 1 с помощью табличного процессора ms Excel
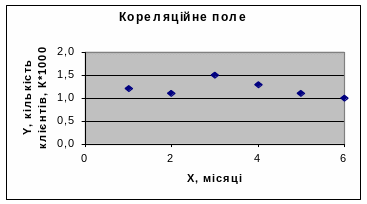
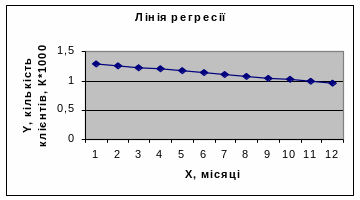
1. Сделать форму для задачи в виде табл. 1 (рис. 1.3). 2. Ввести выходные данные задачи в форму (рис. 1.4). 3. Определить вид функциональной зависимости путем построения графика в виде корреляционного поля (рис. 1.4): • выделить диапазон данных В3:В8 (значение Y); • вызвать «Мастер диаграмм»; • выбрать тип диаграммы - точечная; • диапазон данных: диапазон В3:В8, ряды в столбцах; • ряд: значение Х - А3:А8, значение Y - В3:В8; • заголовки: название диаграммы - Корреляционное поле; ось Х - Х, месяцы; ось Y - Y, количество клиентов, К*1000; • оси: ось Х (категорий), ось Y (значений); • линии сетки: ось Y (значений) - основные линии; • легенды нет; • подписи значений нет; • поместить график на имеющемся листе. Для перехода между отдельными шагами «Мастера диаграмм» необходимо щелкнуть мышкой на кнопке «Далее» или «Назад»; по окончании построения графика - щелкнуть на кнопке «Готово». 4. Определить коэффициент корреляции r (рис. 1.4): курсор в ячейку В9, вызвать «Мастер функций» fx, категория - «Статистические», функция - КОРРЕЛ, «Массив 1» - выделить мышкой диапазон данных А3:А8 (значение Х), «Массив 2»- выделить мышкой диапазон данных В3:В8 (значение Y). 5. Определить коэффициенты регрессии: 5.1. В меню «Сервис» выбрать пункт «Анализ данных», в списке "Инструменты анализа» выбрать «Регрессия» и щелкнуть мышкой на кнопке «ОК». 5.2. В окне «Регрессия» ввести: • входной интервал Y - выделить мышкой диапазон данных В3:В8 (значение Y); • входной интервал Х - выделить мышкой диапазон данных А3:А8 (значение Х); • параметры вывода - новый рабочий лист; • «ОК». 5.3. С листа 4 скопировать вычисленные значения коэффициентов регрессии (ячейка В17 - b0, ячейка В18 - b1) и вставить в лист 1 в ячейки В10 (b0) и В11 (b1) (рис. 1.4). Получено уравнение регрессии Y = 1,32 - 0,03Х. 6. Построить табл. 2 и заполнить ее первый столбец в диапазоне А20:А31 числами от 1 до 12 (рис. 1.5). 7. Вычислить точки графика регрессии (рис. 1.5): • курсор в ячейку В20, ввести формулу "=$В$10+$В$11*А20", нажать "Enter"; • скопировать содержимое ячейки В20 и вставить в ячейки В21:В31 (содержимое ячеек подсчитывается автоматически). 8. Построить график регрессии (рис. 1.5): • выделить диапазон данных В20:В31 (значение Y); • вызвать «Мастер диаграмм»; • выбрать тип диаграммы - точечная со значениями, которые соединяются сглаживающими линиями; • диапазон данных: диапазон В20:В31, ряды в столбцах; • ряд: значение Х - А20:А31, значение Y - В20:В31; • заголовки: название диаграммы - Линия регрессии; ось Х - Х, месяцы; ось Y - Y, количество клиентов, К*1000; • оси: ось Х (категорий), ось Y (значений); • линии сетки: ось Y (значений) - основные линии; • легенды нет; • подписи значений нет; • поместить график на имеющемся листе. Для перехода между отдельными шагами «Мастера диаграмм» необходимо щелкнуть мышкой на кнопке «Далее» или «Назад»; по окончании построения графика - щелкнуть на кнопке «Готово». Готовый график отформатировать. 9. Результаты решения задачи приводятся на рис. 1.5.
Значение коэффициента корреляции -0,36 показывает, что связь между временем и количеством обслуженных клиентов обратная (со временем количество клиентов уменьшается), слабая (течение времени несущественно влияет на изменение количества клиентов). Согласно полученного уравнения регрессии y=1,32-0,03x прогнозируется уменьшение количества обслуженных клиентов около 30 человек каждый месяц, что свидетельствует о нецелесообразности расширения производственных мощностей предприятия в ближайшее время.
|
A |
B |
C |
D |
E |
F |
G |
H |
1 |
|
Таблиця 1 |
|
|
|
|
|
|
2 |
X, міс. |
Y, кіл-ть кл-тів, К*1000 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
9 |
r |
|
|
|
|
|
|
|
10 |
b0 |
|
|
|
|
|
|
|
11 |
b1 |
|
|
|
|
|
|
|
Рис. 1.3. Форма для розв’язання задачі методом кореляційно-регресивного аналізу
|
A |
B |
C |
D |
E |
F |
G |
H |
1 |
|
Таблиця 1 |
|
|
|
|||
2 |
X, міс. |
Y, кіл-ть кл-тів, К*1000 |
|
|
||||
3 |
1 |
1,2 |
|
|
||||
4 |
2 |
1,1 |
|
|
||||
5 |
3 |
1,5 |
|
|
||||
6 |
4 |
1,3 |
|
|
||||
7 |
5 |
1,1 |
|
|
||||
8 |
6 |
1,0 |
|
|
||||
9 |
r |
-0,35857 |
|
|
||||
10 |
b0 |
1,32 |
|
|
||||
11 |
b1 |
-0,03 |
|
|
||||
12 |
|
|
|
|
||||
13 |
|
|
|
|
||||
14 |
|
|
|
|
||||
15 |
|
|
|
|
||||
Рис. 1.4. Введення вихідних даних у форму, побудова кореляційного поля, розрахунок коефіцієнтів кореляції та регресії
|
A |
B |
C |
D |
E |
F |
G |
H |
1 |
|
Таблиця 1 |
|
|
|
|||
2 |
X, міс. |
Y, кіл-ть кл-тів, К*1000 |
|
|
||||
3 |
1 |
1,2 |
|
|
||||
4 |
2 |
1,1 |
|
|
||||
5 |
3 |
1,5 |
|
|
||||
6 |
4 |
1,3 |
|
|
||||
7 |
5 |
1,1 |
|
|
||||
8 |
6 |
1,0 |
|
|
||||
9 |
r |
-0,35857 |
|
|
||||
10 |
b0 |
1,32 |
|
|
||||
11 |
b1 |
-0,03 |
|
|
||||
12 |
|
|
|
|
||||
13 |
|
|
|
|
||||
14 |
|
|
|
|
||||
15 |
|
|
|
|
||||
16 |
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
18 |
|
Таблиця 2 |
|
|
|
|||
19 |
X |
Y=1,32-0,03X |
|
|
||||
20 |
1 |
1,29 |
|
|
||||
21 |
2 |
1,26 |
|
|
||||
22 |
3 |
1,23 |
|
|
||||
23 |
4 |
1,20 |
|
|
||||
24 |
5 |
1,17 |
|
|
||||
25 |
6 |
1,14 |
|
|
||||
26 |
7 |
1,11 |
|
|
||||
27 |
8 |
1,08 |
|
|
||||
28 |
9 |
1,05 |
|
|
||||
29 |
10 |
1,29 |
|
|
||||
30 |
11 |
1,26 |
|
|
||||
31 |
12 |
1,23 |
|
|
||||
32 |
|
|
|
|
||||
33 |
|
|
|
|
||||
34 |
|
|
|
|
|
|
|
|
Рис. 1.5. Результати прогнозу та графік регресії