2.2.Линейная корреляция

Предположим, известно, что случайные величины Х и Y связаны линейной корреляционной зависимостью (обе линии регрессии прямые). Требуется по опытным данным найти уравнения прямых линий регрессии Х на Y и Y на Х и оценить силу линейной корреляционной связи.

Рассмотрим сначала простейший случай, когда в результате независимых опытов была получена совокупность n пар чисел (x₁,y₁), (x₂,y₂), … , (x_n,y_n) (каждая пара чисел наблюдалась только по одному разу). Тогда искомое уравнение прямой линии регрессии Y на Х будет иметь вид:

,

(2.3)

где - выборочный коэффициент регрессии Y на Х.

Уравнение (2.3) называют выборочным уравнением прямой линии регрессии Y на Х. Будем находить параметры и b уравнения (2.3), основываясь на методе наименьших квадратов, т.е. такими, чтобы сумма квадратов отклонений опытных значений y_i от значений (i=1,2, … , n), вычисленных по уравнению (2.3), была минимальной:

Метод наименьших квадратов описан в разделе 2.3.

Система нормальных уравнений для определения и b имеет вид :

(2.4)

Решив эту систему, найдём искомые параметры:

	;	(2.5)
	.	(2.6)

Аналогично можно найти выборочное уравнение прямой линии регрессии X на Y:

Х= ,

(2.7)

где - выборочный коэффициент регрессии Х на Y.

Для характеристики силы линейной корреляционной связи между величинами Х и Y по опытным данным находим выборочный коэффициент корреляции :

,

(2.8)

где

S_X, S_Y – выборочные средние квадратические отклонения:

.

(2.9)

Для практического использования более удобным являются формулы:

	;	(2.10)
	;	(2.11)
	.	(2.12)

Проверка значимости коэффициента корреляции изложена выше.

Пример 2.2. Термодинамические характеристики гидратации ионов в растворе – энтальпия и энтропия для ряда ионов имеют значения, представленные в табл. 2.3 (Y= ; Х= ). Найти зависимость энтальпии Y от энтропии Х и вычислить выборочный коэффициент корреляции.

Решение. Представим в табл.2.3, кроме исходных данных, результаты вычислений коэффициентов системы (2.4). Подставим из табл.2.3 вычисленные суммы в (2.5) и (2.6) найдём значения и b = 260,58. Следовательно, искомое уравнение регрессии Y на Х будет иметь вид: Y=10,96Х + 260,58.

Выборочный коэффициент корреляции найдём по формуле (2.8), предварительно вычислив по формулам (2.10 –2.12):

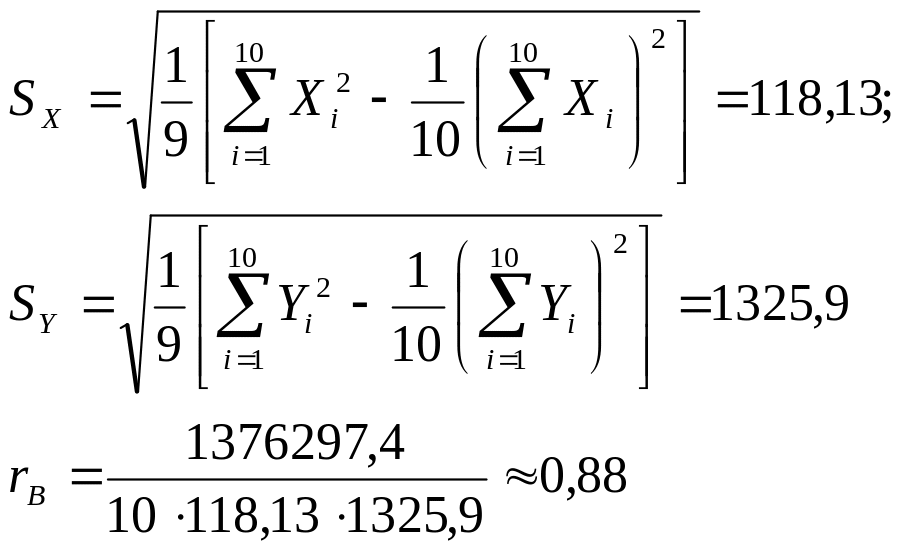
Коэффициент корреляции значимый, т.к. произведение H =r = 0.88 = 2.64 больше табличного для уровня значимости 0.95 (H_табл=1.90).

Таблица 2.3

Исходные данные и результаты вычислений коэффициентов системы (2.4)

I	Ион	Хi кДж /(моль ∙К)	Yi кДж/моль
1	Ва2+	-134	-1329	17956	1766241	178086
2	Be2+	-239	-2516	57121	6330256	601324
3	Ca2+	-184	-1613	33856	2601769	296792
4	Co2+	-258	-2041	66564	4165681	526578
5	Cr3+	-422	-4618	178084	21325924	1948796
6	Fe3+	-418	-4476	174724	20034576	1870968
7	In3+	-394	-4194	155236	17589636	1652436
8	La3+	-364	-3328	132496	11075584	1211392
9	Pb2+	-130	-1516	16900	2298256	197080
10	Sr2+	-171	-1503	29241	2259009	257013
		-2714	-27134	862178	89446932	8740465

Таким образом, можно считать достаточно тесной линейную зависимость энтальпии и энтропии для любых ионов, т.к. это подтвердилось для десяти различных ионов.

По аналогии с примером 2.2 в курсовой работе необходимо исследовать наличие линейной связи между двумя физическими свойствами из приведенных в задании ко второй части курсовой работы (например, Х_i=ρ_i; Y_i=μ_i или Х_i=μ_i; Y_i=Ср_i).
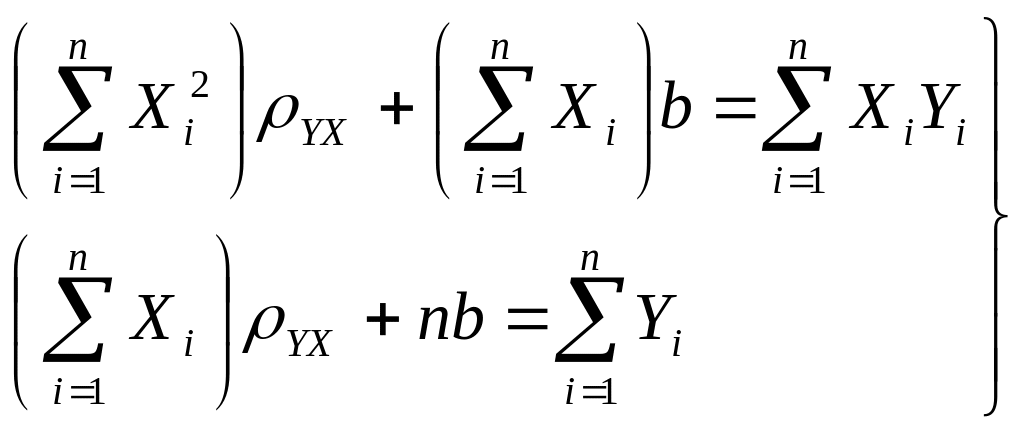
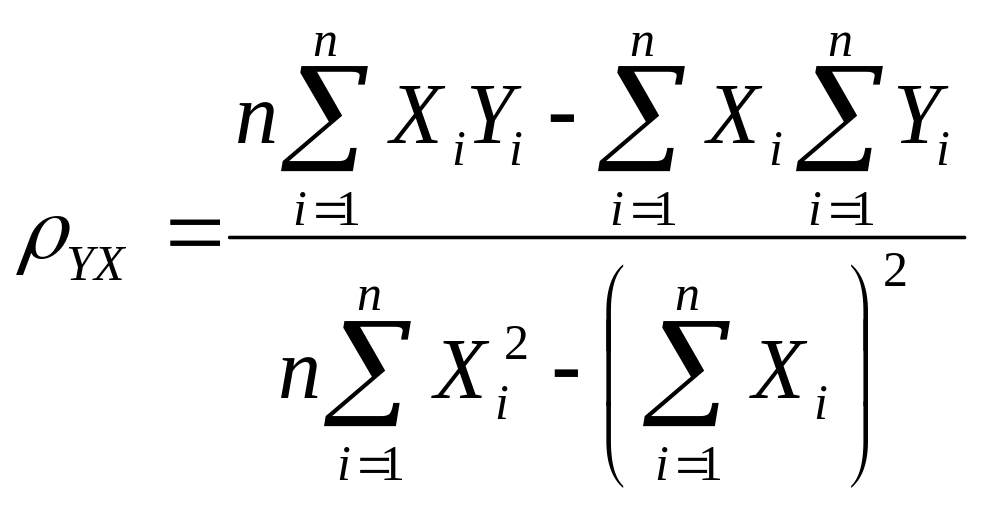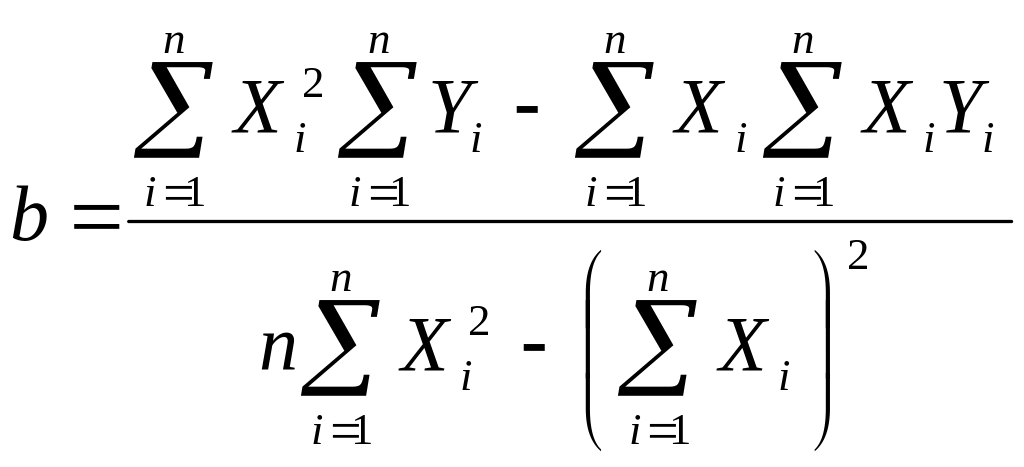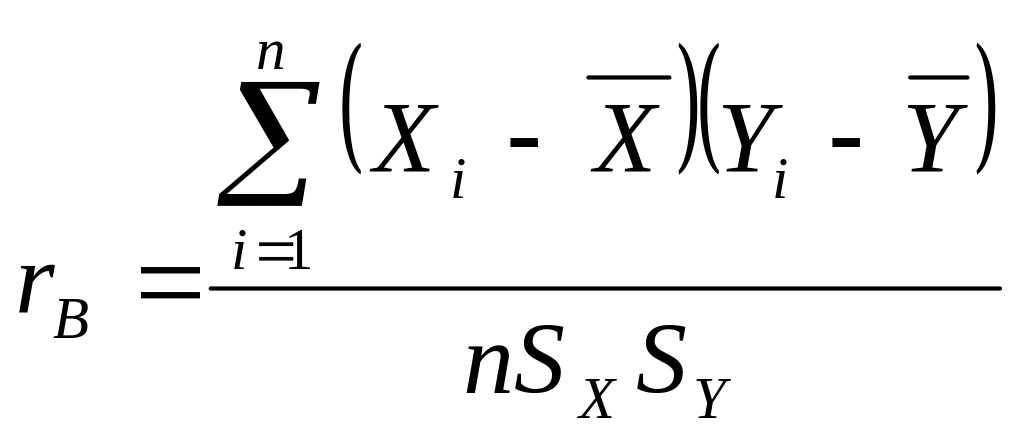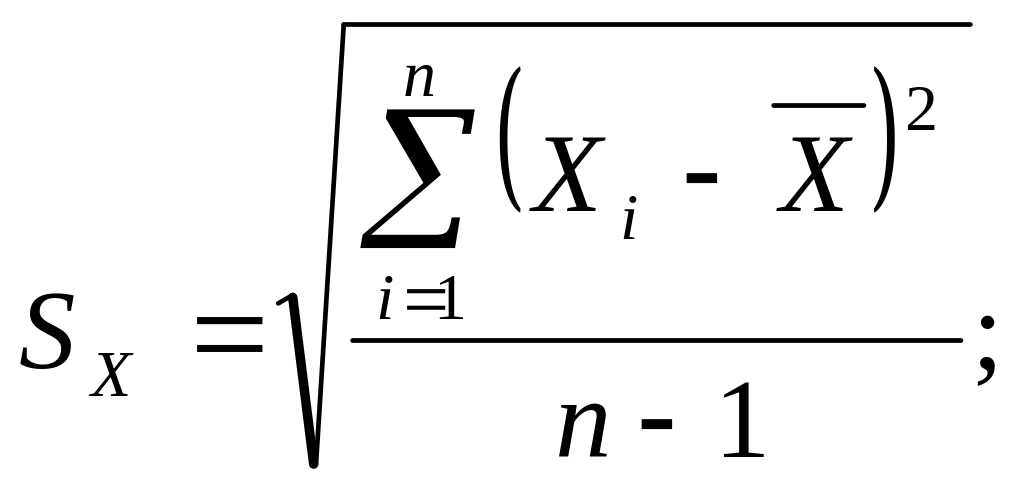
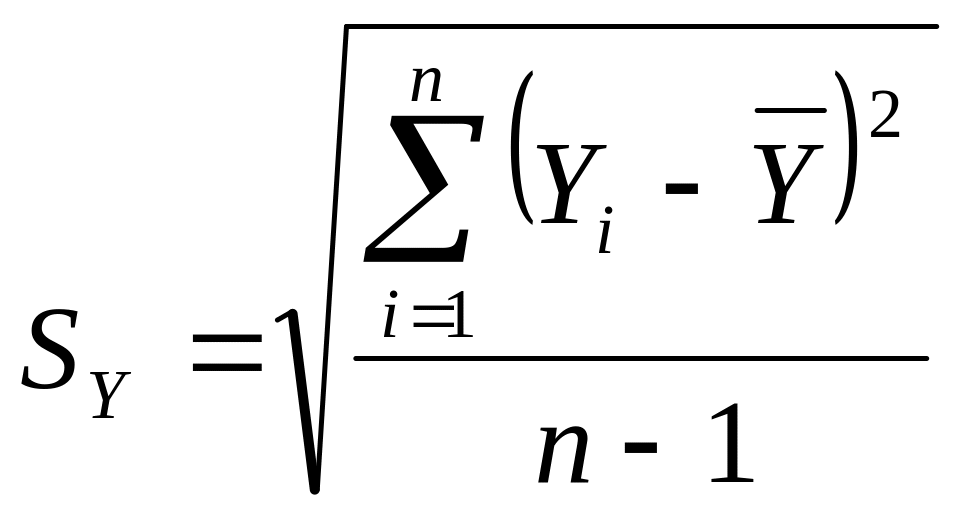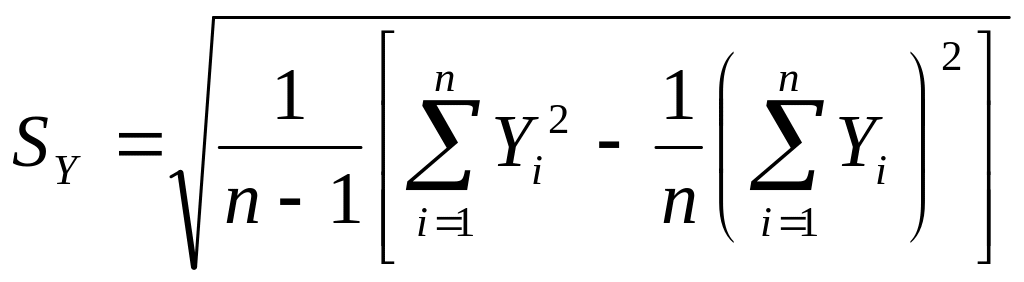