2. Силовой расчет механизма

2.2.1. Силовой расчет структурной группы звеньев 4-5

Строим вначале кинематическую схему механизма для заданного значения угла поворота кривошипа первого цилиндра =120^о. Показываем звенья лишь двух цилиндров двигателя – первого и седьмого (рис. П.7).

Рядом со схемой механизма располагаем две индикаторные диаграммы дизельного двигателя внутреннего сгорания. Перпендикулярно осям ОВ и ОС цилиндров двигателя располагаем оси давлений P газов в цилиндрах, а параллельно осям ОВ и ОС цилиндров – оси перемещений S ползунов . Диаграммы располагаем так, чтобы начало координат было на уровне крайних верхних положений точек В и С, а крайние нижние точки диаграмм на осях перемещений ползуна S были на уровне нижних крайних положений точки В и С. Строим диаграммы в одинаковом произвольном масштабе по оси давления газов Р.

Давление газов в цилиндре двигателя в конце периода сгорания топлива дано по заданию: P =7,0 МН/м . Этому давлению соответствует на диаграмме отрезок у_max = 48,8 мм. Поэтому масштаб по оси давлений газов Р:

.

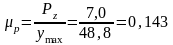
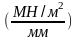Строим в масштабе схему структурной группы звеньев 4-5 (рис. 6.30, а). Прилагаем к звеньям схемы все внешние и внутренние нагрузки. Рассматриваем цилиндр 7 двигателя, в котором идет такт рабочего хода.

Давление газов в цилиндре 7 определяется величиной ординаты 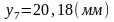на индикаторной диаграмме двигателя внутреннего сгорания (рис. П.7), соответствующей положению точки С ползуна 5 для такта рабочего хода.

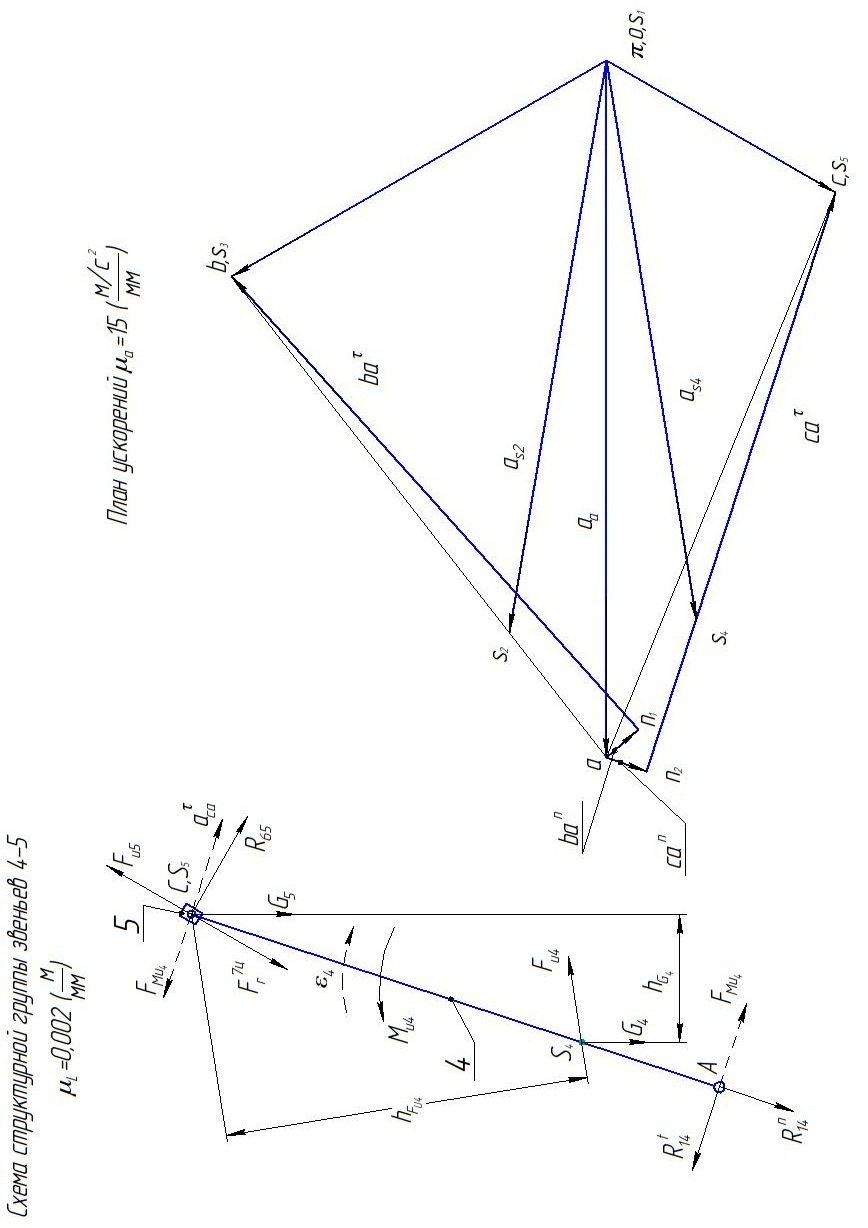
а) б)

Рис. 6.30. Схема структурной группы звеньев 4-5 (а) и план ускорений (б) механизма двигателя

Давление газов в цилиндре 7:

р₇= .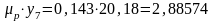

Площадь днища поршня:

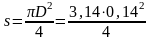=0,015386 (м²).

Сила давления газов на ползун 5 в седьмом цилиндре

F^7ц_г= p₇ s = 2,88574•10⁶•0,015386 = 44400 (H).

Эта сила является силой движущей, приложена к ползуну 5 (см. рис. 6.30, а) и направлена вниз вдоль оси СО цилиндра (см. рис. 6.29, а).

Вычисляем силы тяжести звеньев 4 и 5:

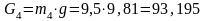(Н),

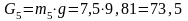(H).

Прилагаем силы тяжести в центрах тяжести звеньев, направляя их вертикально вниз (см. рис. 6.30, а).

Силы инерции звеньев

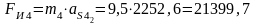(H);

(Н).

Каждую силу инерции звена прилагаем в центре тяжести этого звена (см. рис. 6.30, а) и направляем вектор этой силы параллельно, но противоположно вектору ускорения центра тяжести, имеющемуся на плане ускорений механизма (см. 6.30, б).

Моменты сил инерции звеньев 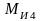и 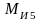определяем через моменты инерции и 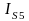и угловые ускорения звеньев 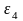и .

Вычисляем величину углового ускорения шатуна 4:

(c^-2).

Для определения направления проводим на схеме структурной группы звеньев 4-5 (см. рис. 6.30, а) пунктирной линией из точки С вектор ускорения точки С относительно условно неподвижной точки А. Угловое ускорение звена СА направлено в ту же сторону, что и вектор , то есть по направлению движения часовой стрелки.

Момент инерции шатуна дан по заданию: = 0,075 ( ).

Момент сил инерции шатуна 4:

(Нм).

Момент сил инерции шатуна 4 направляем противоположно направлению углового ускорения звена 4, то есть против направления движения часовой стрелки (см. рис. 6.30, а).

Для ползуна 5 имеем

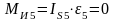, так как .

Определяем теперь внутренние силы, то есть силы реакций в кинематических парах структурной группы звеньев 4-5. Найдем силы реакций во вращательной кинематической паре А (см. рис. 6.30, а) соединения звеньев 1 и 4 и в поступательной паре соединения ползуна 5 со стойкой 6.

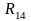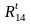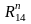Реакцию во вращательной кинематической паре А раскладываем на две составляющие: тангенциальную , которую проводим перпендикулярно линии шатуна АС, и нормальную , которую проводим параллельно линии шатуна АС. Направления стрелок векторов этих составляющих выбираем произвольно, и в дальнейшем эти направления уточняются.

Реакцию 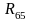прилагаем к ползуну 5 в точке С перпендикулярно боковой стенке ползуна. Направление стрелки вектора этой реакции также выбираем произвольно, и в дальнейшем это направление уточняется.

Определение реакций производим в принятой последовательности для рассматриваемого вида структурной группы звеньев.

1. Сумму всех моментов сил, действующих относительно центра вращательной кинематической пары С на звено 4, приравниваем нулю: 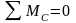. Вычисляется тангенциальная составляющая реакции во вращательной паре А.

;

( ).

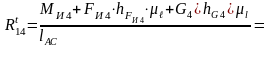
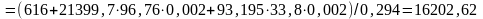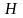2. Векторная сумма всех сил, действующих на звенья 4 и 5, приравнивается нулю: .

.

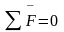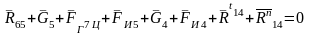В соответствии с уравнением в масштабе сил строится план сил, на котором находят нормальную составляющую реакции и полную реакцию в крайней вращательной кинематической паре А и реакцию в поступательной паре: 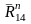, 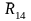и 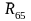. План сил (рис. 6.31) строим в масштабе .

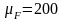
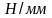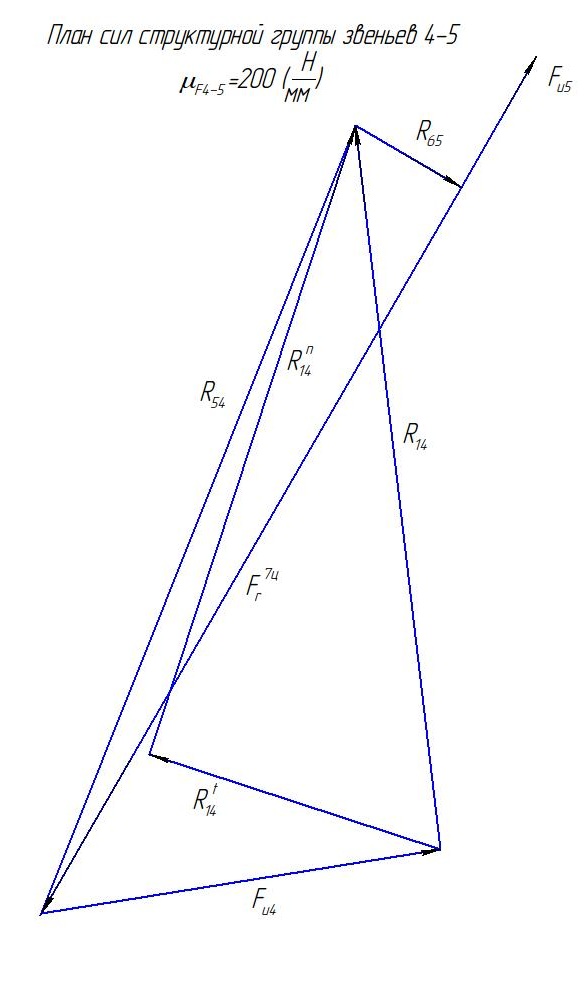
Рис. 6.31. План сил структурной группы звеньев 4-5

Чтобы определить длину вектора известной силы, величину этой силы делим на этот масштаб. Например, силу давления газов на ползун 5 в цилиндре 2 откладываем на плане сил в виде отрезка длиной

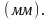
Векторы известных сил откладываем один за другим. Силы тяжести звеньев отсутствуют на плане сил, так как длина их векторов в выбранном масштабе сил получилась менее одного миллиметра.

Из начальной точки построения (см. рис. 6.31) проводим прямую линию вектора реакции , перпендикулярную линии ОС схемы механизма, а из конечной точки построения проводим прямую линию, параллельную вектору . Находим точку пересечения этих линий. Эта точка определяет величины неизвестных реакций. В соответствии с векторным уравнением сил изображаем стрелки векторов этих реакций. Проводим также линию вектора полной реакции , которая равна сумме ее нормальной и тангенциальной составляющих.

Находим на плане неизвестные реакции, умножая измеренные на плане длины соответствующих векторов на масштаб плана сил:

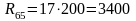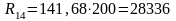(Н);

(Н).