
- •Структурный и кинематический анализ механизма
- •2.1.1. Планы положений механизма
- •Определение степени подвижности и структурный анализ механизма
- •2.1.3. Кинематические диаграммы движения ползуна
- •Планы скоростей механизма
- •Планы ускорений механизма
- •Силовой расчет механизма
- •2.2.1. Силовой расчет структурной группы звеньев 4-5
- •2.2.2. Силовой расчет структурной группы звеньев 2-3
- •2.2.3. Силовой расчет входного звена
- •Проверка правильности выполнения силового расчета по теореме н.Е. Жуковского
- •Синтез и анализ зубчатых механизмов
- •Внешнее неравносмещенное эвольвентное зацепление цилиндрических зубчатых колес
- •Синтез планетарной зубчатой передачи
- •Картина линейных скоростей точек звеньев планетарной зубчатой передачи
- •План угловых скоростей звеньев планетарной зубчатой передачи
- •1.1. Планы положений механизма…………………………… 3
Планы ускорений механизма
Необходимо построить планы ускорений кривошипно-ползунного механизма лишь для двух цилиндров двигателя внутреннего сгорания (рис. 6.29, а).
Строим план ускорений для того положения механизма, для которого по заданию дано значение угла =120о поворота кривошипа, то есть для четвертого положения механизма.
Рассматриваем
вначале ускорения точек входного звена
АО. Ускорение точки О равно нулю, так
как эта точка неподвижна при работе
механизма:
 На плане ускорений вектор
На плане ускорений вектор
 поэтому отсутствует; точка
поэтому отсутствует; точка
 на плане ускорений совпадает с полюсом
на плане ускорений совпадает с полюсом
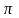 (см. рис.6.29, б).
(см. рис.6.29, б).

а)
)
б)
)
Рис. 6.29. Кинематическая схема кривошипно-ползунного механизма двигателя (а)
и план ускорений (б)
Для определения ускорения точки А составляем векторное уравнение ускорений:
 .
.
Величину тангенциальной составляющей ускорения определяем по формуле
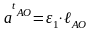 ,
,
где
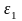 – угловое ускорение звена 1, на котором
расположены рассматриваемые точки,
– угловое ускорение звена 1, на котором
расположены рассматриваемые точки,
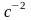 ;
;
 – расстояние между точками А и О, м.
– расстояние между точками А и О, м.
По
заданию вращение входного звена механизма
(кривошипа АО) равномерное, поэтому
тангенциальная составляющая ускорения
точки А относительно точки О равна нулю.
Так как
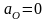 и
и
 то
то
 .
.
Величину этого ускорения определяем по формуле

 .
.
Вектор
(см. рис. 6.29, б) параллелен линии АО звена
1 на схеме механизма (см. рис. 6.29, а) и
направлен от точки А, движение которой
рассматривается, к точке О, принятой в
качестве полюса. Задаемся длиной этого
вектора и проводим этот вектор. Принимаем
 Тогда масштаб плана ускорений будет
Тогда масштаб плана ускорений будет


Рассматриваем далее точки структурной группы звеньев 2-3: А, В и В6.
В поступательной кинематической паре соединения звеньев 3 и 6 взяты две точки: подвижная точка В, принадлежащая звену 3, и неподвижная точка В6, принадлежащая звену 6 (стойке). Обе эти точки в рассматриваемое мгновение по положению совпадают.
Ускорение точки В необходимо определить. Ускорения же двух остальных точек известны: ускорение точки А найдено, и его вектор на плане ускорений уже проведен, ускорение же точки В6 стойки равно нулю.
Составляем систему двух векторных уравнений ускорений:
 ;
;
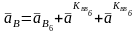 .
.
Приравниваем правые части этих двух уравнений, так как левые части их равны:

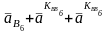 .
.
Вычисляя
кориолисово ускорение, видим, что оно
равно нулю, так как ползун 3 и направляющая
стойки 6, входящие в поступательную
кинематическую пару, вращательного
движения совершать не могут:


Так
как
 и
и
 ,
то векторное уравнение для ускорений
точек механизма можно представить в
виде
,
то векторное уравнение для ускорений
точек механизма можно представить в
виде
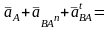
 .
.
Определяем
величину и направление нормальной
составляющей ускорения
 :
:
 ,
,
где

Вектор
 (см. рис. 6.29, б) параллелен линии BА
звена на схеме механизма и направлен
от точки В, движение которой рассматривается,
к точке А, принятой в качестве полюса.
(см. рис. 6.29, б) параллелен линии BА
звена на схеме механизма и направлен
от точки В, движение которой рассматривается,
к точке А, принятой в качестве полюса.
Так
как по уравнению эту составляющую
необходимо прибавить к ускорению
 ,
то на плане ускорений точка
на конце вектора
будет началом вектора
.
Определяем длину этого вектора с
учетом
принятого масштаба плана ускорений:
,
то на плане ускорений точка
на конце вектора
будет началом вектора
.
Определяем длину этого вектора с
учетом
принятого масштаба плана ускорений:
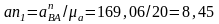 (
( ).
).
Проводим
этот вектор. По уравнению необходимо
далее прибавить вектор тангенциальной
составляющей ускорения
 ,
поэтому из точки
,
поэтому из точки
 плана ускорений (см. рис. 6.29, б) проводим
линию вектора
плана ускорений (см. рис. 6.29, б) проводим
линию вектора
 .
Направление этого вектора известно:
он перпендикулярен прямой ВА схемы
механизма, а величину вычислить не
представляется возможным, так как
угловое ускорение звена АВ неизвестно.
.
Направление этого вектора известно:
он перпендикулярен прямой ВА схемы
механизма, а величину вычислить не
представляется возможным, так как
угловое ускорение звена АВ неизвестно.
По
уравнению на плане ускорений необходимо
провести еще релятивное ускорение
 ,
направление которого известно: оно
параллельно направляющей относительного
поступательного движения звеньев 3 и
6, то есть параллельно линии ОВ механизма
(см. рис. 6.29, а). Величина вектора неизвестна.
,
направление которого известно: оно
параллельно направляющей относительного
поступательного движения звеньев 3 и
6, то есть параллельно линии ОВ механизма
(см. рис. 6.29, а). Величина вектора неизвестна.
Из полюса плана ускорений (см. рис. 6.29, б) проводим линию вектора параллельно направляющей относительного поступательного движения звеньев 3 и 6, то есть параллельно линии ОВ механизма. Находим точку пересечения этой линии с линией вектора . Это точка плана ускорений. В соответствии с уравнением обозначаем стрелки векторов ускорений на плане ускорений.
Находим положение точек s2 и s3 центров тяжести шатуна 2 и ползуна 3 на плане ускорений. Считаем, что точки В и S3 у механизма совпадают. Аналогичные точки должны совпадать и на плане ускорений. По заданию имеем следующее соотношение размеров длин на схеме механизма:
AS2/AB=0,26.
По теореме подобия для планов ускорений аналогичное соотношение соответствующих размеров должно быть и на плане ускорений. Отсюда
 (
).
(
).
Откладывая это расстояние на плане ускорений, получаем точку s2. Соединяя точку полюса плана ускорений с найденной точкой s2, получаем вектор ускорения точки S2.
Ускорения центров тяжести шатуна и ползуна:
 ,
,
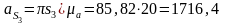 .
.
Рассматриваем далее точки структурной группы звеньев 4-5: А, С и С6. В поступательной кинематической паре соединения звеньев 5 и 6 взяты две точки: подвижная точка С, принадлежащая звену 5, и неподвижная точка С6, принадлежащая звену 6 (стойке). Обе эти точки в рассматриваемое мгновение по положению совпадают.
Ускорение точки С необходимо определить. Ускорения же двух остальных точек известны: ускорение точки А найдено, и его вектор на плане ускорений уже проведен, ускорение же точки С6 стойки равно нулю. Составляем систему двух векторных уравнений ускорений:
 ;
;
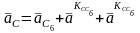 .
.
Приравниваем правые части этих двух уравнений, так как левые части их равны:

 .
.
Вычисляя
кориолисово ускорение, видим, что оно
равно нулю, так как ползун 5 и направляющая
стойки 6, входящие в поступательную
кинематическую пару, вращательного
движения совершать не могут:


Так
как
 и
и
 ,
то векторное уравнение для ускорений
точек механизма можно представить в
виде
,
то векторное уравнение для ускорений
точек механизма можно представить в
виде

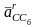 .
.
Определяем
величину и направление нормальной
составляющей ускорения
 :
:
 (
( )
,
)
,
где
 (
).
(
).
Вектор
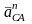 (см. рис. 6.29, б) параллелен линии СА звена
на схеме механизма (см. рис. 6.29, а) и
направлен от точки С, движение которой
рассматривается, к точке А, принятой в
качестве полюса.
(см. рис. 6.29, б) параллелен линии СА звена
на схеме механизма (см. рис. 6.29, а) и
направлен от точки С, движение которой
рассматривается, к точке А, принятой в
качестве полюса.
Так как по уравнению эту составляющую необходимо прибавить к ускорению , то на плане ускорений точка на конце вектора будет началом вектора . Определяем длину этого вектора с учетом принятого масштаба плана ускорений:
 (
).
(
).
Проводим
этот вектор. По уравнению необходимо
далее прибавить вектор тангенциальной
составляющей ускорения
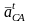 ,
поэтому из точки
,
поэтому из точки
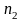 плана ускорений (см. рис. 6.29,б) проводим
линию вектора
.
Направление этого вектора известно:
он перпендикулярен прямой СА схемы
механизма, а величину вычислить не
представляется возможным, так как
угловое ускорение звена АС неизвестно.
плана ускорений (см. рис. 6.29,б) проводим
линию вектора
.
Направление этого вектора известно:
он перпендикулярен прямой СА схемы
механизма, а величину вычислить не
представляется возможным, так как
угловое ускорение звена АС неизвестно.
По
уравнению на плане ускорений необходимо
провести еще релятивное ускорение
 ,
направление которого известно: оно
параллельно направляющей относительного
поступательного движения звеньев 5 и
6, то есть параллельно линии ОС механизма
(см. рис. 6.29, б). Величина вектора неизвестна.
,
направление которого известно: оно
параллельно направляющей относительного
поступательного движения звеньев 5 и
6, то есть параллельно линии ОС механизма
(см. рис. 6.29, б). Величина вектора неизвестна.
Из
полюса плана ускорений
проводим линию вектора
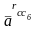 параллельно направляющей относительного
поступательного движения звеньев 5 и
6, то есть параллельно линии ОС механизма.
Находим точку пересечения этой линии
с линией вектора
параллельно направляющей относительного
поступательного движения звеньев 5 и
6, то есть параллельно линии ОС механизма.
Находим точку пересечения этой линии
с линией вектора
 .
Это точка
плана ускорений. В соответствии с
уравнением показываем стрелки векторов
ускорений на плане ускорений.
.
Это точка
плана ускорений. В соответствии с
уравнением показываем стрелки векторов
ускорений на плане ускорений.
Находим положение точек s4 и s5 центров тяжести шатуна 4 и ползуна 5 на плане ускорений. Считаем, что точки С и S5 у механизма совпадают. Аналогичные точки должны совпадать и на плане ускорений. По заданию имеем следующее соотношение размеров:
AS4/AС=0,26.
По теореме подобия для планов ускорений аналогичное соотношение соответствующих размеров должно быть и на плане ускорений. Отсюда
 (
).
(
).
Откладывая это расстояние на плане ускорений, получаем точку s4. Соединяя точку полюса плана ускорений с найденной точкой s4, получаем вектор ускорения точки S4й.
Ускорения центров тяжести шатуна и ползуна:
 ,
,
 .
.
На рис. П.6 приведен вид первого листа курсового проекта.
