1 Способ решения (по уравнению (1)):

Формально из (1) можно записать для последовательности I:

, (2)

а для последовательности II:

или , (3)

Р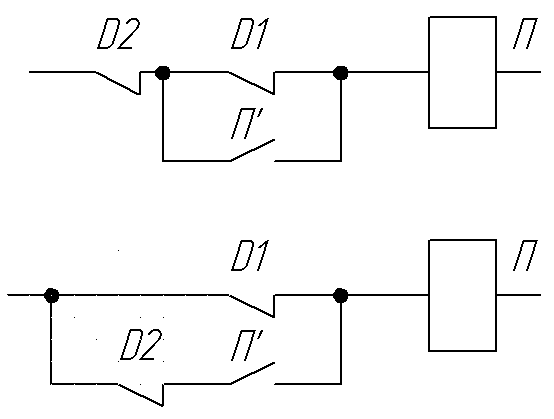 еализация уравнений (2) и (3) на контактных элементах имеет вид: (см. рис). Легко убедиться, что обе схемы удовлетворяют последовательностям тактов. Отличие здесь в обработке ситуации, когда откажет датчик Д1. Пусть он выдает 0, тогда при Д2=1 верхняя схема (2) отключит питатель, а затем при Д2=0 снова его включит, т.е. будем иметь частое включение П. Нижняя схема (3) при Д2=1, а Д1=0 приведет к переполнению резервуара, что является аварийной ситуацией. Поэтому в схеме (3) ситуацию можно считать аварийной и вводить соответствующую защиту.

2 Способ – с помощью карт Карно

Шаги применения способа:

1. Содержательное описание в виде перечня отличающихся друг от друга тактов – уже сделано.

2. Составление таблицы переходов.

В данном примере имеем 2 входа Д1 и Д2 и два возможных состояния выхода 1 – питатель включен, 2 – питатель выключен. Таблица переходов будет иметь следующий вид:

Исходное состояние	Такты
	1	2	3	4
Питатель включен (1)	1	1	2	Х
Питатель выключен (2)	1	2	2	Х
Д1
Д2

Х – ситуация, невозможная при исправном Д1.

3. Выбор числа вспомогательных функций и привязка их к соответствующим состояниям. Число вспомогательных переменных (функций) γ при числе состояний S определяется как . Здесь же осуществляется привязка вспомогательной функции к состояниям, например с помощью таблицы соответствия.

В данном примере S=2, γ=1. Таблица соответствий состояний и вспомогательной переменной x_в, которую можно считать равной выходному сигналу П, имеет вид:

N состояния	Значение вспом. пер. xв=П
1	1
2	0

4. Построение карт Карно для входных переменных и вспомогательных переменных и синтез алгебраических выражений.

Число столбцов в карте Карно такое же, как и в таблице переходов, а число строк равно числу комбинаций вспомогательных переменных (2^). Клетки карты заполняются значениями вспомогательной функции, полученными путем замены номера состояния из таблицы переходов на значение вспомогательной функции из таблицы соответствия. Если число строк превышает число состояний (2^>S), то свободные строки заполняются из соображений лучшей минимизации.

Для рассмотренного примера, карта Карно выглядит так:

		D1		D2
xв		1	1	0	*01/12
		1	0	0	*01/12

Если принять, что при Д2=1, Д1=0 (случай неработающего Д1) питатель должен быть отключен (т.е. в * должен быть 0), получим (считая x_в=П):

- совпадает с (2).

Если принять, что при Д2=1, Д1=0 питатель включается – аварийный режим, то получим:

- совпадает с (3).

4. Наконец, на пятом шаге производится реализация на выбранной элементной базе.

Пример 2:

Рассмотрим синтез последовательностного алгоритма для выше рассмотренного примера с подъемником. Первые два пункта уже были выполнены – содержательное описание с разбивкой на такты и таблица переходов.

Таблица переходов:

Исходное состояние		Такты (наборы)
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Движ. вверх (1)		3	3	3	3	3	3	3	3	1	1	1	1	1	1	1	1
Движение вниз (2)		3	3	3	3	2	2	2	2	2	2	2	2	3	3	3	3
Кабина стоит (3)		3	3	3	3	3	3	2	3	3	2	3	1	1	3	3	3
Мнемо-схема	ПН
	ПВ
	РН
	РВ

Третий шаг – выбор вспомогательных переменных и привязка их к состояниям.

Здесь S=3, тогда  будет равно 2 (х_в1 и х_в2). Таблица соответствия (примем х_в1 В и х_в2Н):

Состояние	хв1	хв2
1	1	0
2	0	1
3	0	0
-	1	1

Четвертая комбинация вспомогательных переменных нереальна, т.к. не может быть одновременного движения вверх и вниз.

Четвертый шаг – составление карты Карно и минимизация. Для движения вверх (выход В, 1-ое состояние) х_в1=В. В карте Карно будет 64 клетки (16x4).

хв1					0		0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
хв2					0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
				0			0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
				0			0	0	0	0	0	0	0	0	0	0	1	1	0	0	0
ПН
ПВ
РН
РВ

Тогда

Аналогично для движения вниз:

хв1					0		0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
хв2					0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
				0			0	0	0	1	1	1	1	1	1	1	1	0	0	0	0
				0			0	0	0	0	0	1	0	0	1	0	0	0	0	0	0
ПН
ПВ
РН
РВ

Тогда

Пятый шаг – реализация.