3. Обнаружение многоуровневых аномалий

3.1 Многомерный способ обратных вероятностей для обнаружения заданных по форме аномалий

Как и для одномерного варианта способа обратных вероятностей, форму аномалии по каждому полю получают либо из решения прямых задач, либо по визуально наблюденным аномалиям, а величину дисперсии помехи оценивают на заведомо безаномальном участке. Тогда, по аналогии с одномерным вариантом способа обратных вероятностей, функция правдоподобия для ненулевой гипотезы H₁ примет вид

,

а для нулевой гипотезы

.

Отношение правдоподобия , с учетом этих выражений и предположения о некоррелированности помехи для разных полей

.

(2)

При >1 выполняется гипотеза H₁, при   1 - гипотеза H₀. Переход от отношения правдоподобия к апостериорной вероятности наличия аномалии р(H₁/Y) осуществляется по формуле Байеса (формула обратных вероятностей), которая в данном случае выглядит как

.

При > 0,5 принимается решение о наличии комплексной аномалии А_i, при < 0,5 - об ее отсутствии.

Надежность обнаружения  комплексной аномалии вычисляется с помощью интеграла вероятности Ф, для которого верхним пределом служит обобщенное энергетическое отношение аномалия/помеха , т.е.

,

(3)

В качестве примера расчета квадратичной формы приведем случай для двух полей. Пусть для одного из них аномалия фиксируется значениями a₁₁ = 1; a₁₂= 3; a₁₃ = 1, а дисперсия помехи D₁ = 3, для другого – аномалия a₂₁ = 0,2; a₂₂ = 0,5; a₂₃= 0,2 , а для дисперсии помехи D₂ = 0,05. Тогда величина определяется следующим образом:

.

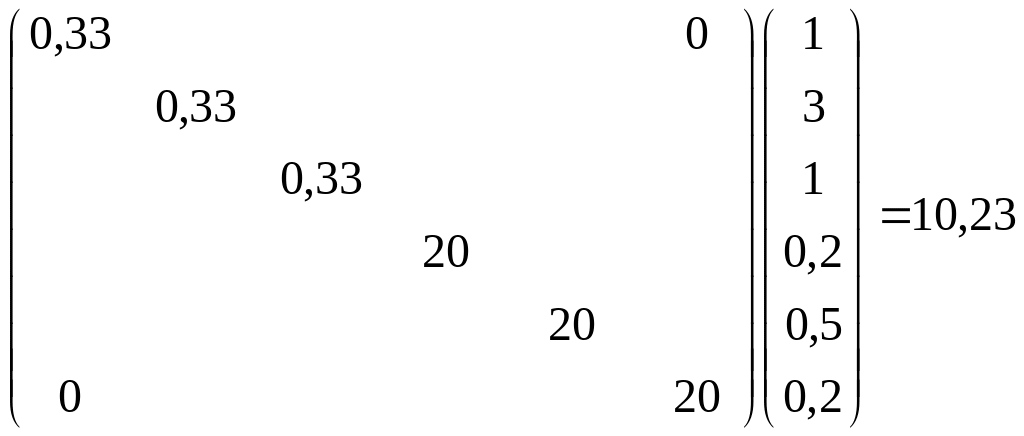Согласно выражению (3) значение надежности обнаружения комплексной аномалии  равно 95%, тогда как по первому полю =81% (₁=3,63), а по второму  = 87% (₂=6,6). Совершенно аналогично величине рассчитывается выражение в формуле (2), в которой компонентами вектора являются наблюденные значения по т точкам каждого поля (уровня). В том случае, когда имеются наблюдения по разным методам и по разным уровням одновременно, корреляционная матрица D становится блочной, а векторы А_i, и Y_i, превращаются в матрицы [см. формулу (2)].

3.2 Многомерный способ самонастраивающейся фильтрации [7]

Математическая модель многомерного аналога способа самонастраивающейся фильтрации состоит в том, что, как и для одномерного варианта, рассматривается окно размером в т пикетов и N профилей. При различных положениях окна, т.е. при различных наклонах окна по отношению к простиранию профилей, проверяется нулевая гипотеза H₀ о средних значениях в столбцах окна (гипотеза об отсутствии комплексной аномалии). При этом наблюденные значения в окне представляют собой не одиночные значения одного поля, а векторы наблюдений размерности L, где L - число одновременно обрабатываемых полей или уровней.

При отсутствии комплексной аномалии модель поля в каждой точке наблюдения определяется многомерной нормально распределенной помехой с нулевым вектором среднего и ковариационной матрицей D, а при наличии аномалии - модель поля есть сумма комплексной аномалии и той же многомерной помехи.

Для данной модели возможно построение критериальной статистики так называемого следа матрицы T², которая позволяет решить вопрос о том, равны ли векторы средних во всех столбцах окна нулевому вектору (гипотеза H₀) или же некоторые из них отличны от нулевого вектора (гипотеза H₁). Для проверки гипотезы H₀ статистика следа матрицы T² имеет вид:

,

(4)

где R и G^-1 – случайные матрицы, имеющие распределение Уишарта.

Для многомерного аналога самонастраивающейся фильтрации оценкой матрицы R размерности (mNL) (mNL) является выражение

,

(5)

где Y_i оценка вектора среднего в i-ом столбце окна, т.е. ; и т.д. Такие оценки вычисляются по каждому полю. Например, когда имеются только два поля, матрица R выражается как

.

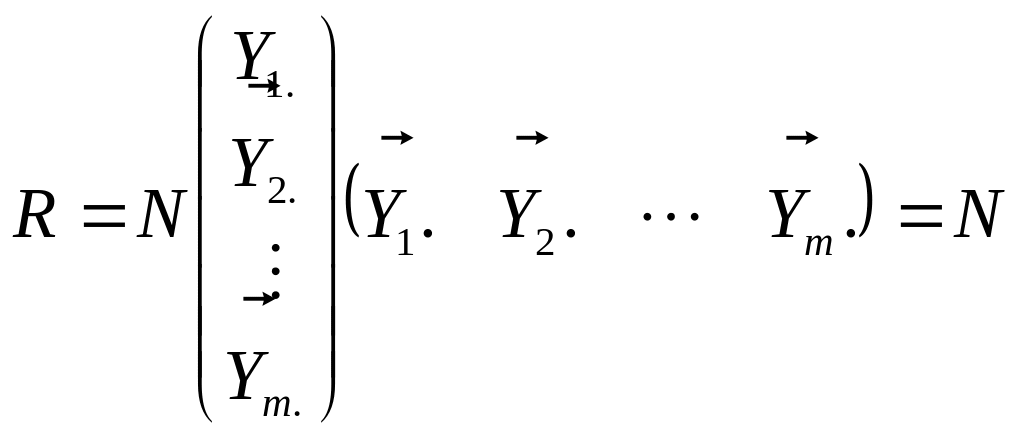
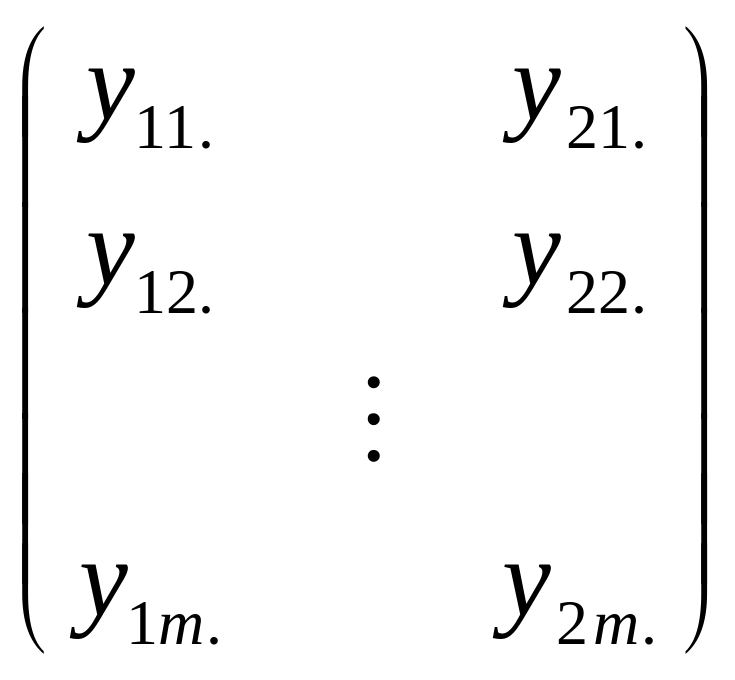
Матрица G размерности (mNL) (mNL) определяется формулой

.	(6)

Ковариационная матрица D связана с G соотношением

,

где m - число столбцов в окне (число пикетов); N – число строк в окне (число профилей).

Статистика следа матрицы T² аппроксимируется статистикой Фишера F и обе эти статистики связаны между собой соотношением

Представляя из выражений (5) и (6) выражения для R и G в (4), получим критериальную статистику многомерного аналога самонастраивающейся фильтрации

(7)

В случае выполнения нулевой гипотезы H₀, гипотезы об отсутствии комплексной аномалии, статистика (7) распределена приближенно по закону Фишера со степенями свободы

.

Гипотеза о равенстве векторов средних в столбцах окна нулю отвергается, если F > F _g1,g2,_ где  – заданный уровень значимости. При этом принимается решение о наличии комплексной аномалии в окне, т.е. решение о выполнении гипотезы H₁.