Примеры выполнения тестовых заданий

Задание 1. Установите соответствие уравнений Шредингера их физическому смыслу: 1. нестационарное                                           А.    2. стационарное для микрочастицы              Б.    в одномерной потенциальной яме 3. стационарное для электрона                       В. 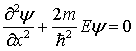   в водородоподобном атоме 4. стационарное для гармонического             Г.       осциллятора                                                                            Д.

1) 1-В, 2-Б, 3-А, 4-Д	2) 1-Г, 2-В, 3-А, 4-Б
3) 1-А, 2-Б, 3-Г, 4-В	4) 1-Г, 2-Д, 3-А, 4-Б

Выполнение задания. Нестационарное или временное уравнение Шредингера – основное дифференциальное уравнение квантовой механики относительно волновой функции , зависящей от координат и времени. Оно определяет -функцию для микрочастиц, движущихся в силовом поле с потенциальной энергией U(x,y,z,t), и имеет вид

,

где – оператор Лапласа, m – масса частицы, , h – постоянная Планка. - мнимая единица.

В случае, когда -функция не зависит от времени , она удовлетворяет стационарному уравнению Шредингера

,

где Е – энергия частицы.

В одномерной потенциальной яме шириной l (см. рисунок) потенциальная энергия микрочастицы внутри ямы равна нулю, т. е. U = 0 при . Учитывая, что для одномерной задачи , стационарное уравнение Шредингера принимает вид

.

В атоме электрон движется в кулоновском поле ядра с зарядом Ze и обладает потенциальной энергией, равной

,

где r – расстояние между электроном и ядром, ε₀ – электрическая постоянная.

Стационарное уравнение Шредингера для электрона в водородоподобном атоме имеет вид

.

Потенциальная энергия гармонического осциллятора равна

,

где m – масса частицы, ω₀ – собственная частота колебаний осциллятора.

Стационарное уравнение Шредингера для гармонического осциллятора имеет вид

.

Следовательно, правильное соответствие уравнений Шредингера их физическому смыслу: 1-Г, 2-В, 3-А, 4-Б.

Ответ: 2) 1-Г, 2-В, 3-А, 4-Б

6.4. Уравнение шредингера (конкретныеситуации)

При выполнении тестовых заданий студент должен знать: плотность вероятности обнаружения микрочастицы.

уметь: находить вероятность обнаружения электрона в некоторой области одномерного потенциального ящика с бесконечно высокими стенками.

Примеры выполнения тестовых заданий

Задание 1. Волновая функция ( пси-функция), описывающая состояние частицы в одномерной потенциальной яме имеет вид, указанный на рисунке. Вероятность обнаружить электрон на участке  равна… 1) 5/6 2) 2/3 3) 1/3 4) 1/2

Выполнение задания. Вероятность обнаружить электрон на участке одномерной потенциальной ямы вычисляется по формуле , а это есть площадь под кривой плотности вероятности обнаружения электрона. В соответствии с условием задания (см. рисунок) на ширине ямы укладывается 3 полуволны, т.е. электрон находится на третьем энергетическом уровне.

На представленном графике вероятность его обнаружения на заданном участке, изображена в виде заштрихованной площади, а это составляет 2/3 от всей площади.

Ответ: 2)