1.2 Методичний приклад

Розглянемо приклад. Нехай задана z-передавальна функція

.

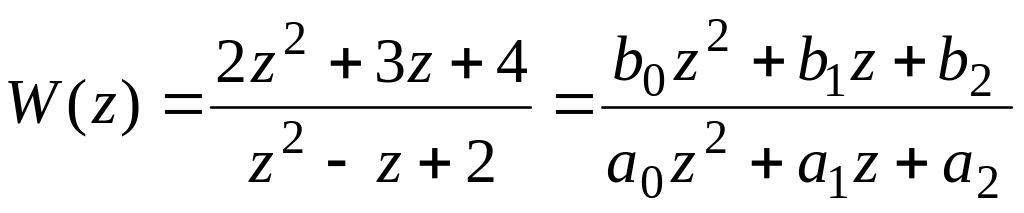Запишемо відповідне різницеве рівняння

,

введемо змінну стану

,

.

Позначимо

,

.

З останнього рівняння виразимо

,

та підставимо в рівняння стану для і

Запишемо отриману систему в векторно-матричній формі

, .

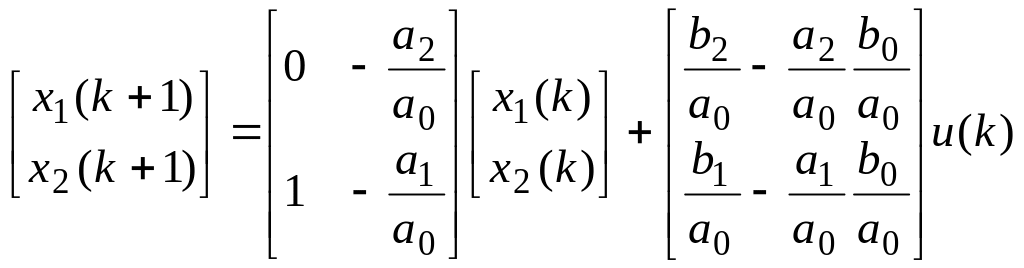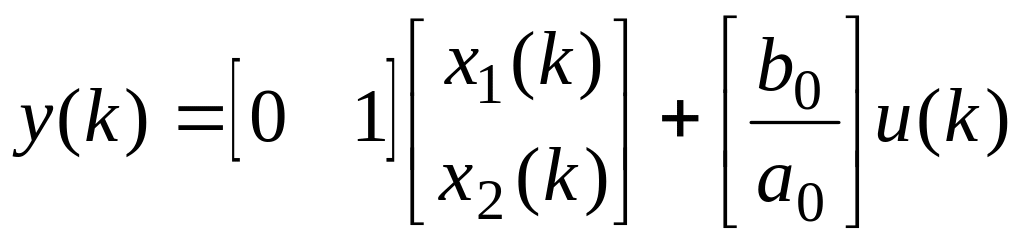Тобто

, ,

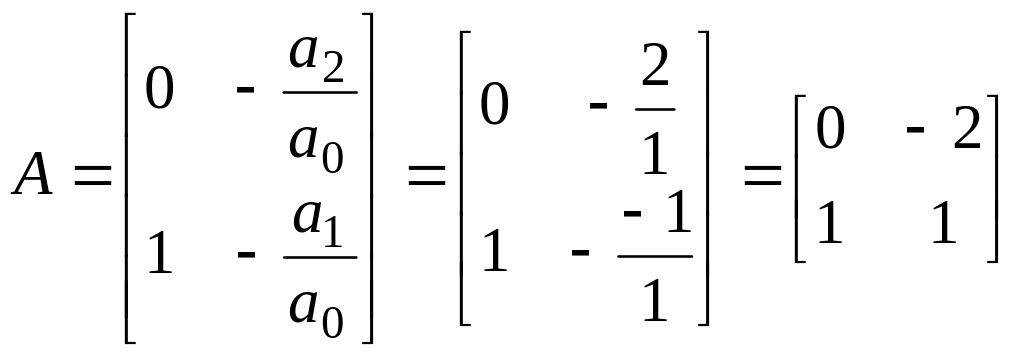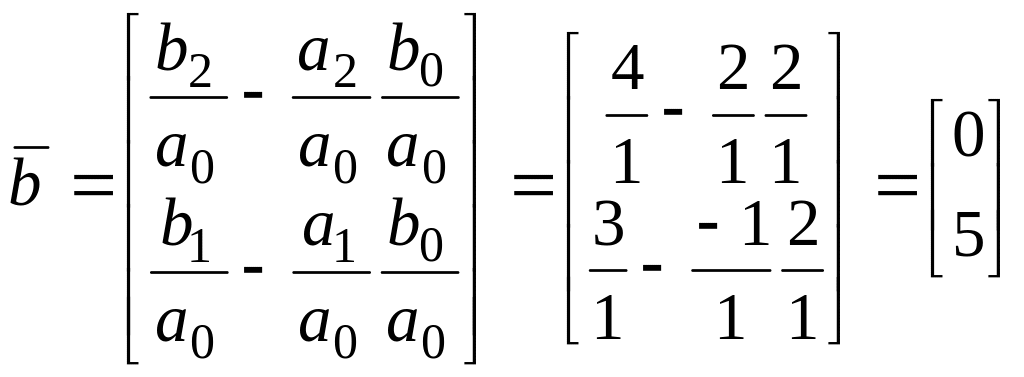та .

1.2 Одержання рівняння стану дискретної динамічної системи на основі рівняння безперервної системи

Якщо відомо рівняння стану безперервної системи

(12)

тоді рівняння стану дискретної системи може бути представлено в формі:

. (13)

де – матриця переходу станів розімкненої дискретної динамічної системи

,

– вектор керуючого переходу дискретної динамічної системи

.

Матрицю переходу стану можливо обчислити при розкладанні матричного експоненціала у нескінченний ряд

. (14)

Для одержання вектора найчастіше використовується розкладання в ряд, що сходиться, модифікованого матричного експоненціала

. (15)

1.3 Дослідження стійкості дискретних систем

На рис. 1 представлена структурна схема досліджувальної в лабораторній роботі системи керування (ФНП – фіксатор нульового порядку, НЧ – неперервна частина).

Рисунок 1 – Структурна схеми системи керування

Найважливішим завданням аналізу динамічних систем керування є вирішення питання про їх стійкості. Проблема стійкості зазвичай виникає в замкнених системах керування через вплив зворотного зв'язку.

Основна умова стійкості: для того щоб лінійна дискретна система керування була стійкою, необхідно та достатньо, щоб всі корені її характеристичного рівняння були по модулю менше одиниці, або, що те ж, перебували всередині окружності одиничного радіуса на z площині коренів.

Період квантування Т впливає на стійкість замкненої системи нарівні з іншими параметрами системи (коефіцієнт передачі, постійні часу тощо). При розрахунку та проектуванні САУ іноді буває необхідним дослідити вплив її різних параметрів на стійкість. Для вирішення цієї задачі служить побудова областей стійкості, тобто визначення таких областей значень параметрів, при яких система виявляється стійкою. Область стійкості можливо визначити використовуючи теоретичні методи або експериментальним чином. Для цього необхідно простим перебором значень параметрів системи керування (в нашому випадку T та k) визначити граничні значення цих параметрів при яких система є стійкою.

Для проведення дослідження доцільно використовувати наступні функції пакету Control System Toolbox: c2d() для отримання дискретної моделі системи; feedback() для отримання опису замкненої системи керування; step() для отримання перехідної функції; pole(), eig() або pzmap() для отримання значень коренів характеристичного рівняння (полюсів).

2. Завдання

Згідно таблиці варіантів необхідно:

1) знайти z - передавальну функцію (1) цифрової системи з урахуванням екстраполятора нульового порядку при номінальному періоду дискретності Т та коефіцієнту передачі k за допомогою функцій пакету MATLAB;

2) отримати рівняння стану (10) та виходу (11) дискретної динамічної системи на основі різницевого рівняння (2);

3) отримати опис безперервного об’єкта керування в простору станів (12) та обчислити матриці переходу стану і вектора керуючого переходу за допомогою формул (14), (15) та функції пакету MATLAB c2d(A,B,T);

4) провести дослідження впливу періоду дискретизації та коефіцієнту передачі на розміщення полюсів замкненої дискретної динамічної системи на z-площині, оцінити її стійкість за допомогою пакету MATLAB;

5) побудувати область стійкості замкненої дискретної системи по параметрам Т та k. Для цього необхідно експериментально знайти такі комбінації значень параметрів (k,Т) при яких система знаходитися на межі стійкості, саме через ці точки буде проходити крива D-розділення;