1.2 Методичний приклад

Нехай, наприклад, вираз у фігурних дужках має наступний вигляд:

.

Використовуючи формули (3) отримують величини коефіцієнтів С₁, С₂ , С₃:

( )

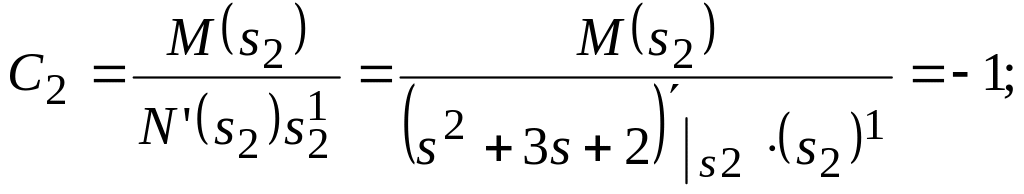
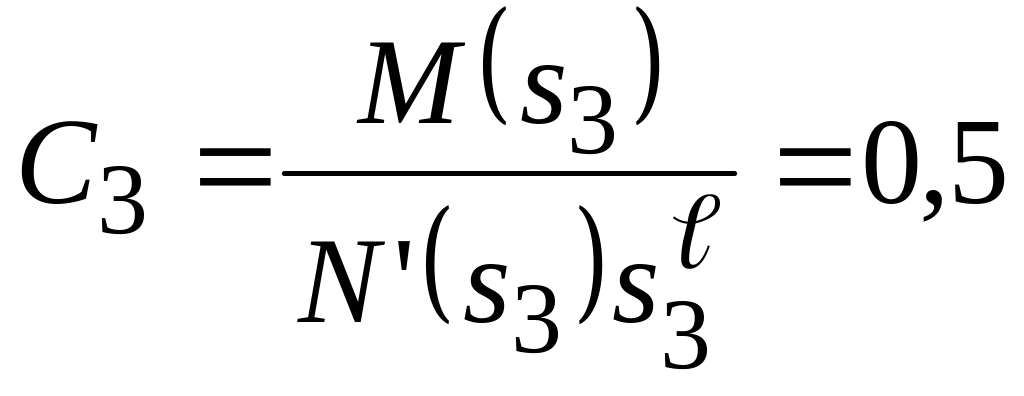Враховуючи таблицю відповідності перетворення Лапласу і z-перетворення, фрагмент якої показаний нижче, знаходять z-перетворення для кожного доданку і отримують відповідну передавальну функцію для заданого періоду дискретності Т:

; ; ;

Для прикладу, який тут розглядається, буде визначеною наступним чином:

.

Після проведення еквівалентних перетворень отримуємо:

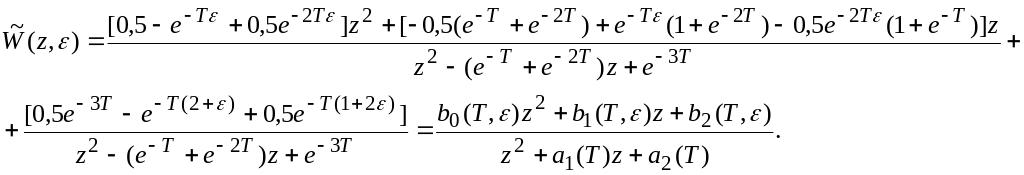
Якщо у даному прикладі прийняти ε = 0 і Т = 0,5 с, то отримаємо

Після підстановки розрахованого значення в формулу (1) отримують z-передавальну функцію розімкненої цифрової системи керування.

2. Завдання

Таблиця 1 – Таблиця варіантів

№ варіанту	Передавальна функція об’єкту	Період дискретності Т, с	Запізнення об’єкту, с
1		2	1
2		0,5	1
3		1	2
4		0,5	1,5
5		5	10
6		0,8	2,4
7		1,5	6
8		1	4
9		1	2
10		1,5	3

Згідно таблиці варіантів необхідно:

1) отримати передавальну функцію і запізнення об’єкту керування;

2) розрахувати без урахування запізнення , а потім визначити z-передавальну функцію розімкненої цифрової системи з урахуванням запізнення;

3) для контролю одержаних результатів розрахувати коефіцієнти передавальної функції і для ε = 0;

4) зробити висновки по роботі.

3. Зміст звіту

У звіти представити:

1. Варіант завдання.

2. Привести необхідні послідовні розрахунки, яки дозволяють отримати передавальні функції і з урахуванням передавальної функції формуючого елементу.

3. Отримані передавальні функції і для ε = 0.

4. Висновки по роботі.

Лабораторна робота № 2 «Дослідження розімкненої імпульсної системи керування»

Мета роботи: полягає в тому, щоб студенти набули навичок математичного опису імпульсної системи, здобуття модифікованого z–преобразованія для дискретних сигналів, а також навики використання Matlab для моделювання імпульсної системи.

1. Теоретичні відомості

Розглядається розімкнена імпульсна система, яка показана на рис. 1. Необхідно знайти реакцію такої системи на послідовність миттєвих імпульсів , утворених з безперервної вхідної дії в дискретні моменти часу. Реакція розширеної безперервної системи, яка складається з формуючого елементу нульового порядку і безперервної частини, на імпульс одиничної площі є імпульсною перехідною функцією або ваговою функцією . Якщо миттєвий імпульс виникає в момент (тобто він зміщений за часом), то і реакція виникає в той же момент часу.

Рисунок 1 – Розімкнена імпульсна система

Реакція лінійної розширеної безперервної системи на послідовність миттєвих імпульсів знаходиться як сума реакцій на окремі імпульси, зміщені за часом:

. (1)

Якщо дослідника цікавлять значення вихідної величини лише в дискретні моменти часу , тобто , то для її здобуття замість необхідно підставити дискретну імпульсну перехідну функцію :

(2)

Вихідна величина на відміну від вхідної відображається зміщеною гратчастою функцією, яка залежить від . Завдяки цьому по рівнянню (2) можна знайти значення вихідної величини у будь-який момент часу , якщо при заданому значенні змінювати від 0 до 1.

Якщо врахувати, що z-перетворенням вхідного сигналу , що містить стрибки, є , а z-зображення зміщеної гратчастої функції на виході системи - , то дискретна передавальна функція розімкненої імпульсної системи буде

. (3)

Формулу (3) зручно використовувати для визначення у будь-який момент часу , якщо заздалегідь знайти z-перетворення вхідного сигналу і дискретну передавальну функцію . Тоді

. (4)

Слід звернути увагу на те, що якщо вхідний сигнал не містить стрибків, то дискретна передавальна функція розімкненої імпульсної системи визначається як

, (5)

і відповідно модифікується рівняння (4). По отриманих виразах для , а вони є дрібно-раціональними функціями, коефіцієнти яких залежать від , досить просто розрахувати значення вихідної величини у будь-який момент часу .